Datawhale组队学习之西瓜书task3

第四章 决策树

4.1 决策树的基本流程

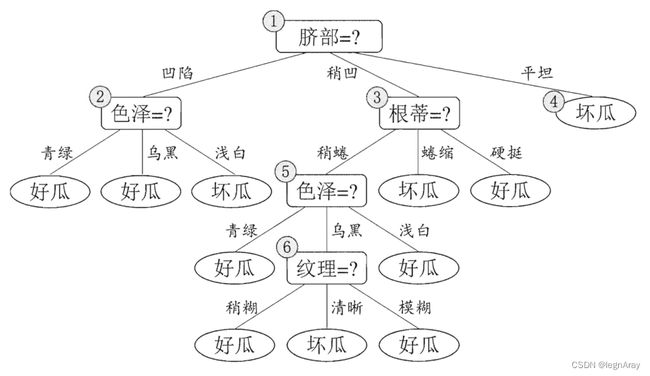
决策树（decision tree）是一种常见的机器学习方法，形如下图所示：

一般情况下，一棵决策树包含了一个根结点（上图结点1），若干个内部结点（上图结点2356），以及若干个叶结点（上图结点4等）。

叶结点显示决策结果，其余结点对应一个属性测试。

决策树的基本生成流程如下：

有三种情形会导致函数递归返回：

1. 当前结点全属于同一类别，无需划分：此时将此结点标记为叶结点，类别为此结点内样本所属类别
2. 当前结点无属性值或所有样本的属性值相同，无法划分：此时将此结点标记为叶结点，类别为此结点内比例最高的类别
3. 当前结点无样本，无法划分：此时将此结点标记为叶结点，类别为父结点内比例最高的类别

4.2 常见决策树

决策树的关键在于如何选择最优划分属性，即上图红框部分。

在这里有一个原则：我们希望结点的“纯度”随着划分越来越高，即划分出的结点尽可能属于同一类别

对于“纯度”的数学定义不同，自然也产生了不同的决策树。

4.2.1 ID3决策树

ID3决策树使用信息熵（详细信息参见第三章笔记3.7.4）来度量纯度：
$$\begin{array}{r}\text{Ent}(D)=-\sum _{k=1}^{|\mathcal{Y}|}{p}_k{\text{log}}_2{p}_k\end{array}$$
其中，$p_k$为样本集合$D$中第$k$类样本所占的比例。

$\text{Ent}(D)$越小，$D$的纯度越高。

由信息熵，可以计算出用属性$a$对样本集$D$进行划分所得到的信息增益（information gain）：
$$\begin{array}{r}\text{Gain}(D,a)=\text{Ent}(D)-\sum _{v=1}^V\frac{\left|D^v\right|}{\left|D\right|}\text{Ent}(D^v)\end{array}$$
其中，离散属性$a$有$V$个可能的取值，$D$中属性为$a^v$的样本集合记为$D^v$

ID3决策树选取信息增益最大的属性来进行划分：
$$a^{\ast }=\underset{a\in A}{\text{arg max }}\text{Gain}(D,a)$$

4.2.2 C4.5决策树

C4.5决策树同样以信息熵度量纯度，但是在决策时与ID3决策树有所不同。

考虑到信息增益对可取值数目较多的属性有所偏好（本质上是样本量太少，干扰太大），为了减少其带来的不利影响，使用增益率（gain ratio）来进行属性划分：
$$\begin{array}{rl}\text{Gain}\_\text{ratio}(D,a)& =\frac{\text{Gain}(D,a)}{\text{Int}(a)}\\ \text{Int}(a)& =-\sum _{v=1}^V\frac{\left|D^v\right|}{\left|D\right|}{\text{log}}_2\frac{\left|D^v\right|}{\left|D\right|}\end{array}$$
$\text{Int}(a)$称为属性$a$的固有值（intrinsic value），属性的取值数目越多，其值就越大，相应的增益率就越小。

但增益率对可取值数目较少的属性有所偏好，因此C4.5并不直接通过增益率来决策，而是先从属性中选出信息增益高于平均水平的属性，再从中选择增益率最高的

4.2.3 CART决策树

CART决策树通过基尼值（Gini value）来度量纯度：
$$\begin{array}{rl}\text{Gini}(D)& =\sum _{k=1}^{|\mathcal{Y}|}{p}_k(1-p_k)\\ & =1-\sum _{k=1}^{|\mathcal{Y}|}{p}_k^2\end{array}$$
基尼值反映了从数据集中随机抽取两个样本，其类别不同的概率，因此基尼值越小，数据集纯度越高。

因此，CART决策树通过最小化基尼系数（Gini index）来划分属性：
$$\begin{array}{rl}\text{Gini}\_\text{index}(D,a)& =\sum _{v=1}^V\frac{\left|D^v\right|}{\left|D\right|}\text{Gini}(D^v)\\ a^{\ast }& =\underset{a\in A}{\text{arg min }}\text{Gini}\_\text{index}(D,a)\end{array}$$

4.3 剪枝、连续值、缺失值、多变量

4.3.1 剪枝

剪枝（pruning）是决策树用来对付过拟合的主要手段，分为预剪枝（pre-pruning）与后剪枝（post-pruning）

预剪枝

预剪枝是指在决策树生成过程中，对每个结点在划分前进行估计，如果划分后不能带来准确率提升，那就不进行划分。

优点：降低过拟合风险，显著减少训练时间与测试时间的开销

缺点：增加了欠拟合风险

后剪枝

后剪枝是指先从训练集中生成一棵完整的决策树，然后自底向上对非叶结点进行测试，若将其替换为叶结点可以提升泛化性能，就将其替换为叶结点

优点：降低过拟合风险的同时欠拟合风险小，泛化性能优于预剪枝

缺点：训练时间与测试时间开销过大

4.3.2 连续值处理

对于连续属性$a$，将其所有出现的值从大到小排列，记为$\{a^1,a^2,\cdots ,a^n\}$，可以任取$t\in [a^1,a^n)$，将原集合$D$分为小于等于$t$的$D_t^{-}$与大于$t$的$D_t^{+}$

这里$t$取值比较随意，事实上$t$在$[a^i,a^{i+1})$中取任意值得到的划分结果都相同，因此为了便于度量，基于中点给出一个划分点集合：
$$T_a=\left\{\frac{a^i+a^{i+1}}{2}|1⩽i⩽n-1\right\}$$
这时，我们进行属性划分时，还需要考虑划分点了，这里以信息增益为例：
$$\begin{array}{rl}\text{Gain}(D,a)& =\underset{t\in T_a}{\max }\text{Gain}(D,a,t)\\ & =\underset{t\in T_a}{\max }\text{Ent}(D)-\sum _{\lambda \in \{-,+\}}\frac{\left|D^v\right|}{\left|D\right|}\text{Ent}(D_t^{\lambda })\end{array}$$
意思就是说，在考虑属性划分的时候，要用连续属性最大的信息增益与其他属性的信息增益作比较

需要注意的是，若当前结点划分属性为连续属性，那么其子结点也可以用该属性进行划分，比如父结点“身高>180”、子结点“身高>185”

4.3.3 缺失值处理

对于缺失值，核心的处理思路就是用无缺样本代替总体来进行计算，从而进行划分。

注意，这里“无缺样本”指的并不是“所有属性都完整的样本”，而是对于某一属性，集合内该属性没有缺失的样本（有可能一个样本可以参与属性$a$的计算但是不可以参与属性$b$的计算）

给出新的信息增益计算公式：
$$\begin{array}{rl}\text{Ent}(\tilde{D})& =-\sum _{k=1}^{|\mathcal{Y}|}{\tilde{p}}_k{\text{log}}_2{\tilde{p}}_k\\ \text{Gain}(D,a)& =\rho \times \text{Gain}(\tilde{D},a)\\ & =\rho \times \left(\text{Ent}(\tilde{D})-\sum _{v=1}^V{\tilde{r}}_v\text{Ent}({\tilde{D}}^v)\right)\end{array}$$
其中，对于属性$a$，$\rho$是无缺样本所占比例，${\tilde{p}}_k$是无缺样本中第$k$类样本所占比例，${\tilde{r}}_v$是无缺样本中在属性$a$上取值为$a^v$的所占比例

如果划分属性已经确定，但某样本有属性缺失，该怎么办呢？

答：以${\tilde{r}}_v$为新权重，划分到每个子结点中（每个子结点的权重不同，和为1）

4.3.4 多变量决策树

多变量决策树（multivariate decision tree）的非叶结点是形如${\sum }_{i=1}^d{w}_i{a}_i=t$的线性分类器，不再仅对某个属性，而是对所有属性的线性组合进行测试，其中$w_i,t$都可以通过样本学习得到

对于单变量决策树轴平行的分类边界，多变量决策树的分类边界更加灵活（图中黑色折线为单变量决策树的分类边界）

---

参考资料

周志华：《机器学习》

Datawhale：【吃瓜教程】《机器学习公式详解》（南瓜书）与西瓜书公式推导直播合集