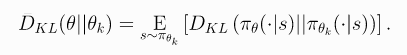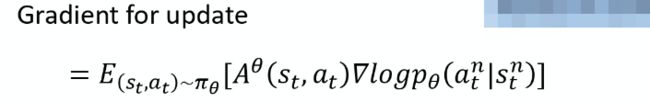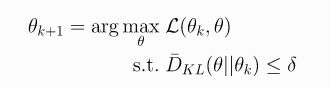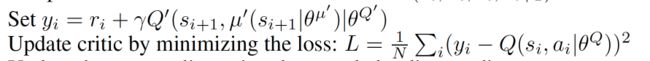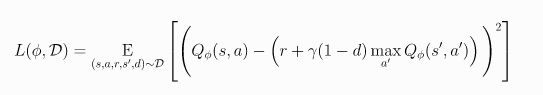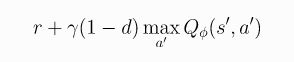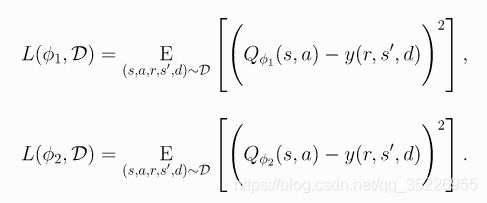强化学习个人学习总结
强化学习
Reinforce Learning,简称RL。RL是利用奖励(reward)驱动代理(agent)在获取环境(env)的状态(state/obs)后做出一些列行动(action),导致环境到达下一个状态并给出这次行动的奖励,以驱动代理进行下一次决策。
文章目录
-
- 强化学习
- 1、基本概念
-
- 1.1 以王者绝悟系统为例:
- 1.2 不同于监督学习(SL)
- 2、强化学习算法
-
- 2.1 算法基础
-
- 2.2.1 符号定义
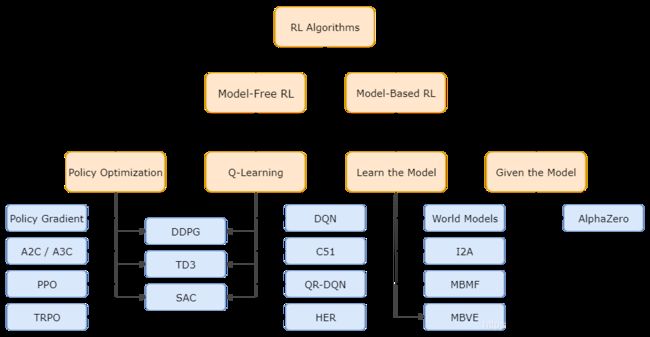
- 2.2.2 算法分类
-
- (1) Model-Free vs Model-Based
- (2) Policy-Based vs Value-Based
- (3) 单步(step)更新 vs 回合(episode)更新
- (4) On-Policy vs Off-Policy
- (5) 强化学习 vs 模仿学习
- 2.2 强化学习
-
- 2.2.1 Value-Based算法
-
- (1) Q-Learning
- (2) Sarsa
- (3) Sarsa( λ \lambda λ)
- (4) Deep Q Network (DQN)
- (5) Double DQN
- (6) Prioritized Experience Replay (DQN)
- (7) Dueling DQN
- 2.2.2 Policy-Based算法
-
- (1) Vanilla Policy Gradient (VPG)
- 2.2.3 Value-Based+Policy-Based算法
-
- (1) Actor Critic
- (2) Trust Region Policy Optimization (TRPO)
- (3) Proximal Policy Optimization(PPO)
- (4) Deep Deterministic Policy Gradient(DDPG)
- (5) Twin Delayed DDPG (TD3)
- (6) Soft Actor-Critic (SAC)
- (7) Asynchronous Advantage Actor-Critic (A2C / A3C)
- 2.3 模仿学习
-
- 2.3.1 行为克隆(Behavior Cloning)
- 2.3.2 逆强化学习(Inverse Reinforcement Learning)
- 2.3.3 生成对抗模仿学习(GAN for Imitation Learning )
1、基本概念
1.1 以王者绝悟系统为例:
- 环境:env,也就是王者峡谷系统
- 代理:agent,可以理解为机器人本身,会观察环境根据算法做出决策(行动),来和环境交互
- 状态:state,可以简单理解为王者峡谷的某一帧,比如这一帧有几个防御塔,防御塔多少血,兵线,英雄,队友,对手,野怪,技能等各种基本单位所处的状态
- 行动:action,即agent在根据env所处的state通过agent内置的RL算法做出的行为,比如位移进塔后使用一技能+三技能+普攻杀死对方英雄后,使用闪现出塔并接二技能清线。每一步的采取的一个行为就是一个action。
- 奖励:reward,即agent做出一个或一系列action后获得的env反馈的奖惩值,比如王者要等到一局游戏结束后才会有给出奖励,例如1(胜利)或0(失败),这种属于稀疏的延迟奖励,需要将最终的奖励更新到agent达到最终结局的每一个action上。而有的则是每个action都有立即反馈的奖励,比如飞机打怪兽游戏。
- 策略:policy,指的是agent可以采取的一系列action的概率集合,比如三个行为(0.1,0.5,0.4),agent会从policy中sample出一个action
- 轨迹:trajectory,值得是一系列状态、行为、奖励的集合,即 τ = { s 0 , a 0 , r 0 , s 1 , a 1 , r 1 , . . . , r T } \tau=\{s_0,a_0,r_0,s_1,a_1,r_1,...,r_T\} τ={s0,a0,r0,s1,a1,r1,...,rT}
下面结合具体的例子分析一下:王者峡谷开局(env)会呈现给机器人(agent)一些初始画面 s 0 s_0 s0(state),然后agent和env进行交互,并做出一些行动 a 0 a_0 a0(action),比如典韦作为打野上路开蓝,假设得到环境给与的奖励为 r 0 r_0 r0(reward,注意这里只是假设,事实上王者并没有这种立即奖励,而是等最终游戏胜负后反向溯源来根据每个action的奖励);在蓝血量只有10%时发现敌方辅助来干扰,因此在该帧状态 s 1 s_1 s1的情况下决定使用“惩戒”技能抢夺野怪,即 a 1 a_1 a1,并获得奖励 r 1 r_1 r1;然后看到上单被抓的状态 s 2 s_2 s2,迅速支援并使用一技能+二技能击杀对方英雄,即 a 2 a_2 a2,获得奖励 r 2 r_2 r2;…;最后直到游戏结束,摧毁敌方水晶获得奖励 r T r_T rT。这样一局游戏叫做一个episode。值得注意的是,王者由于只有等到 r T r_T rT时才会获得真正的环境奖励,而之前的 r 0 , . . . , r T − 1 r_0,...,r_{T-1} r0,...,rT−1都是假设的,因此获得 r T r_T rT后会溯源并更新达到最终状态的每一步的奖励,当然每步奖励的更新幅度会有不同,比如开局开蓝离得太远可能就更新得较少,而中期开团导致对方团灭更新幅度可能更大,而后期开风暴龙王直接导致一波对面导致奖励更新更大。
1.2 不同于监督学习(SL)
- RL没有准确的GT标签,而只有奖励(相当于监督学习的标签)
- SL中网络也可看做是agent,但agent的决策不会影响下一步的决策。比如这次将一张图像判定位猫,不管对错,都不会影响它下一次的判断。而RL则不同,这次看对了,不仅导致下一次看到的画面不同,还会因为得到的奖励不同造成下一次的识别,比如这次看做了打了它一棍子,下一次自然畏畏缩缩的了。
2、强化学习算法
2.1 算法基础
2.2.1 符号定义
- 采取的行动可能是确定性的,也可能是随机的,比如根据Q值选择行为的算法,就很直接选Q值最大对应的action,这一类为确定性策略(deterministic policy);而根据概率选择行为的,就像监督学习那样,最终结果为(0.1,0.5,0.4),在SL预测中直接将类别归为0.5对应的那一类,因为属于这一类的可能性最大,但并不排除属于0.1那一类和0.4那一类的可能性,否则网络识别精度肯定就是1了嘛。而RL中也有这个问题,而且RL不像SL会直接选择0.5对应的那一类,而是根据概率随机选择,也就是说可能最后就选择了0.1对应的那个action,这个概率只是说在重复很多次的情况下,选择三个action的概率为0.1,0.5和0.4而已,这一类则被称为随机性策略(stochastic policy)。
- 对于确定性策略,action和state的关系记为: a t = μ ( s t ) a_t=\mu(s_t) at=μ(st);而对于随机性策略,记为 a t ∼ π ( ⋅ ∣ s t ) a_t\sim\pi(\cdot | s_t) at∼π(⋅∣st)。
- 假设agent网络最后一层输出的概率为 P θ ( s ) P_\theta(s) Pθ(s),则对于网络采取的action为 a a a的对数似然(Log-Likelihood)可以表示为 l o g π θ ( a ∣ s t ) = l o g [ P θ ( s ) ] a log\pi_\theta(a | s_t)=log[P_\theta(s)]_a logπθ(a∣st)=log[Pθ(s)]a。
- 对于对角高斯策略(Diagonal Gaussian Policies)的特殊情况,即 P θ ( s ) P_\theta(s) Pθ(s)服从对角高斯分布(仅对角线上有值,其余全部为0),这种情况下action可以表示为 a = μ θ ( s ) + σ θ ( s ) ⋅ z a=\mu_\theta(s)+\sigma_\theta(s)\cdot z a=μθ(s)+σθ(s)⋅z,其中点乘 ⋅ \cdot ⋅表示元素乘法,而 μ θ ( s ) \mu_\theta(s) μθ(s)和 σ θ ( s ) \sigma_\theta(s) σθ(s)分别表示action的均值和标准差,而 z ∼ N ( 0 , I ) z\sim N(0,I) z∼N(0,I),这种情况下,上面的对数似然 l o g π θ ( a ∣ s ) log\pi_\theta(a | s) logπθ(a∣s)可以特殊化表示为(其中 k k k是action的维度):
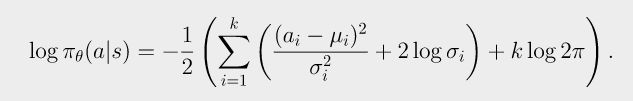
- 第 t t t步骤奖励函数由当前状态、刚刚采取的行动以及下一个状态共同决定,记为 r t = R ( s t , a t , s t + 1 ) r_t=R(s_t,a_t,s_{t+1}) rt=R(st,at,st+1),有时可能也会简化为 r t = R ( s t ) r_t=R(s_t) rt=R(st)和 r t = R ( s t , a t ) r_t=R(s_t,a_t) rt=R(st,at)。
- 而整个episode中的奖励(即与轨迹trajectory有关的函数)可以表示为: R ( τ ) = ∑ t = 0 T r t R(\tau)=\sum_{t=0}^{T}{r_t} R(τ)=∑t=0Trt或 R ( τ ) = ∑ t = 0 ∞ γ t r t R(\tau)=\sum_{t=0}^{\infty}{\gamma^tr_t} R(τ)=∑t=0∞γtrt,其中 γ ∈ ( 0 , 1 ) \gamma\in{(0,1)} γ∈(0,1)。前者有限项无衰减,后者无限项有衰减(越靠后的奖励在整个episode中占据的权重衰减越多)。也有的把这一项 R ( τ ) R(\tau) R(τ)叫做return。
- 对于一个 T T T个step的episode,采取的action和state等组成最终轨迹的概率可以表示为:

- 而对应的Return的期望值可以表示为:

- 和SL类似,SL是让损失最小化,而RL是让奖励Return的期望值最大化,因此优化目标可以表示为:

- 这里的 π \pi π可以理解为policy或者说生成policy的那个网络。
- 值函数Value Functions:可以细分为On-Policy Value Function和On-Policy Action-Value Function,前者表示在状态 s 0 s_0 s0的条件下达到最终 R ( τ ) R(\tau) R(τ)的期望值,称为V值函数;而后者则表示在状态 s 0 s_0 s0和行动 a 0 a_0 a0的条件下达到最终 R ( τ ) R(\tau) R(τ)的期望值,又称为Q值函数。分别表示如下:
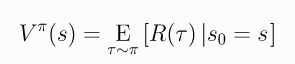
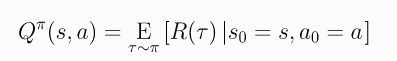
- 而V值函数和Q值函数的关系可以表示为下式(V值函数为Q值函数的期望):
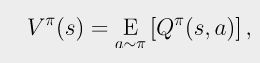
- 可以注意到:最大化Return的均值 J ( θ ) J(\theta) J(θ)和最大化V值函数、最大化Q值函数的效果是一致的。那为了最大化 J ( θ ) J(\theta) J(θ)、 V π ( s ) V^\pi(s) Vπ(s)、 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a),采取的action可以怎么表示呢?即如下:

- 贝尔曼方程(Bellman Equations):可以看到以上所有过程都是定的,做不了文章,那每年发那么多RL的文章是改了什么呢?就是下面的贝尔曼方程(不是改贝尔曼方程本身,贝尔曼方程本身也是固定的,而是改了贝尔曼方程的后续表达形式。比如做不同的近似)。那什么是贝尔曼方程呢?如下:
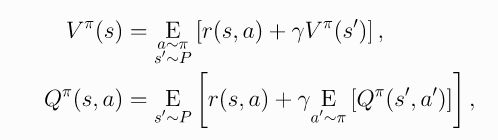
- 其中 s ′ ∼ P s^{'}\sim P s′∼P, a ∼ π a\sim \pi a∼π, a ′ ∼ π a^{'}\sim \pi a′∼π分别表示 s ′ ∼ P ( ⋅ ∣ s , a ) s^{'}\sim P(\cdot|s,a) s′∼P(⋅∣s,a), a ∼ π ( ⋅ ∣ s , a ) a\sim \pi(\cdot|s,a) a∼π(⋅∣s,a), a ′ ∼ π ( ⋅ ∣ s , a ) a^{'}\sim \pi(\cdot|s,a) a′∼π(⋅∣s,a), s ′ s^{'} s′表示 s s s的下一个状态。而最大化 J ( θ ) J(\theta) J(θ)时也就相当于最大化 V π ( s ) V^\pi(s) Vπ(s)或 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a),因此是有必要最大化 V π ( s ) V^\pi(s) Vπ(s)和 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)的,可以表示为:

- 优势函数Advantage Functions:以上的 J ( θ ) J(\theta) J(θ), V π ( s ) V^\pi(s) Vπ(s)和 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)都是衡量一个动作在绝对意义上有多好,但实际中更重要的往往是只需要描述它平均比其他动作好多少,也就是相对有多好,,因此就定义了优势函数,表示为:
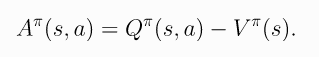
- 啥意思?Q值函数表示某个确定动作的Return,而V值函数表示不同动作的Return的期望(平局值),因此上式表示的也就是某个动作比平均动作好多少!
2.2.2 算法分类
(1) Model-Free vs Model-Based
- Model-Free:不需要对env进行建模,env返回啥状态啥奖励的我不去猜,它给啥就是啥,我做好自己的事,他给的东西我作为GT去训练好自己的模模型,得到一系列在当前条件下最好的action。那自然Model-Based就是去对env进行建模咯~
- 根据莫烦大佬的解释,Model-Based相当于比Model-Free多了模拟环境这个环节,通过模拟环境预判接下来会发生的所有情况,然后选择最佳的情况。
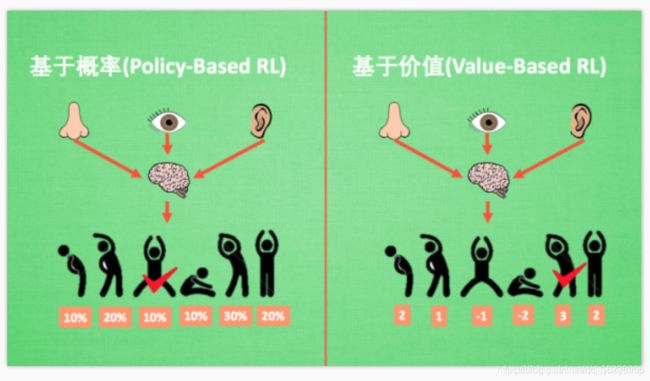
(2) Policy-Based vs Value-Based
- Policy-Based方法:Policy-Based的方法直接输出下一步动作的概率,根据概率来选取采样选择动作,但不一定概率最高就会选择该动作,还是会从整体进行考虑,也就是随机策略(sample,概率小的也可能被挑选,只是被选的概率低一点而已。适用于非连续和连续的动作。常见的方法有policy gradients类的方法,即上图中的Policy Optimization分支。
- Value-Based方法:Value-Based的方法输出的是动作的价值(V值或Q值),选择价值最高的动作。适用于非连续的动作。常见的方法有Q-learning和Sarsa,即上图中的Q-Learning分支。
- 更为厉害的方法是将Policy-Based和Value-Based二者结合的方法:即Actor-Critic,分别训练Actor和Critic两个网络。其中Actor根据概率(Policy)做出动作,Critic根据做出的动作给出价值(V值或Q值),从而加速学习过程。
(3) 单步(step)更新 vs 回合(episode)更新
- 回合更新的方法是指整个学习过程全部结束后再进行更新,常见的方法有Monte-Carlo learning和基础版的policy gradients
- 单步更新的方法是指学习过程中的每一步都在更新,不用等到全部结束后在进行更新。常见的方法有Q-learning、Sarsa和升级版的policy gradients。
- 相比而言,单步更新的方法更有效率。
- 其中回合更新又叫MC方法(Monte-Carlo),而单步更新方法又叫TD方法(Temporal-Difference)。
- 详细推导过程可以参考李宏毅的课程

(4) On-Policy vs Off-Policy
- 在线学习(on-policy)指的是学习的过程agent必须参与其中(更新的agent和与环境交互来产生轨迹的agent是同一个人),典型的算法为Sarsa。
- 离线学习(off-policy)指的是既可以自己参与其中,也可以根据他人学习过程进行学习(更新的agent和与环境交互来产生轨迹的agent不是同一个人)。典型的方法是Q-learning,已经Deep-Q-Network。
(5) 强化学习 vs 模仿学习
- 根据回报函数(reward function)是否已知进行分类。强化学习为已知回报函数。但是当任务十分复杂时,回报函数往往很难确定。而模仿学习则是用来解决这种问题,根据专家实例学习回报函数。
- 模仿学习下可以分为三大类:behavior cloning(行为克隆,类似于监督学习,给出什么样的专家示范,当机器遇到相同的情况时就根据专家的动作进行操作。缺点就是需要大量的专家示范数据集,不然遇到没有见过的情形,实验结果会不好)、invers reinforcement learning(逆强化学习,给定一个专家策略后,来学习寻找最佳的回报函数)和 生成对抗模仿学习(GAN for Imitation Learning, GAIL)。不过,目前来看模仿学习主要集中在逆强化学习上。
[1] A2C / A3C (Asynchronous Advantage Actor-Critic): Mnih et al, 2016
[2] PPO (Proximal Policy Optimization): Schulman et al, 2017
[3] TRPO (Trust Region Policy Optimization): Schulman et al, 2015
[4] DDPG (Deep Deterministic Policy Gradient): Lillicrap et al, 2015
[5] TD3 (Twin Delayed DDPG): Fujimoto et al, 2018
[6] SAC (Soft Actor-Critic): Haarnoja et al, 2018
[7] DQN (Deep Q-Networks): Mnih et al, 2013
[8] C51 (Categorical 51-Atom DQN): Bellemare et al, 2017
[9] QR-DQN (Quantile Regression DQN): Dabney et al, 2017
[10] HER (Hindsight Experience Replay): Andrychowicz et al, 2017
[11] World Models: Ha and Schmidhuber, 2018
[12] I2A (Imagination-Augmented Agents): Weber et al, 2017
[13] MBMF (Model-Based RL with Model-Free Fine-Tuning): Nagabandi et al, 2017
[14] MBVE (Model-Based Value Expansion): Feinberg et al, 2018
[15] AlphaZero: Silver et al, 2017
2.2 强化学习
2.2.1 Value-Based算法
(1) Q-Learning
-
off-policy算法
-
行为准则:我们做事情都会有一个自己的行为准则, 比如小时候爸妈常说”不写完作业就不准看电视”. 所以我们在 写作业的这种状态下, 好的行为就是继续写作业, 直到写完它, 我们还可以得到奖励, 不好的行为 就是没写完就跑去看电视了, 被爸妈发现, 后果很严重. 小时候这种事情做多了, 也就变成我们不可磨灭的记忆. 这和我们要提到的 Q learning 有什么关系呢? 原来 Q learning 也是一个决策过程, 和小时候的这种情况差不多. 我们举例说明:假设现在我们处于写作业的状态而且我们以前并没有尝试过写作业时看电视, 所以现在我们有两种选择 , 1, 继续写作业, 2, 跑去看电视. 因为以前没有被罚过, 所以我选看电视, 然后现在的状态变成了看电视, 我又选了继续看电视, 接着我还是看电视, 最后爸妈回家, 发现我没写完作业就去看电视了, 狠狠地惩罚了我一次, 我也深刻地记下了这一次经历, 并在我的脑海中将 “没写完作业就看电视” 这种行为更改为负面行为, 我们在看看 Q learning 根据很多这样的经历是如何来决策的吧.

-
QLearning 决策:假设我们的行为准则已经学习好了, 现在我们处于状态s1, 我在写作业, 我有两个行为 a1, a2, 分别是看电视和写作业, 根据我的经验, 在这种 s1 状态下, a2 写作业 带来的潜在奖励要比 a1 看电视高, 这里的潜在奖励我们可以用一个有关于 s 和 a 的 Q 表格代替, 在我的记忆Q表格中, Q(s1, a1)=-2 要小于 Q(s1, a2)=1, 所以我们判断要选择 a2 作为下一个行为. 现在我们的状态更新成 s2 , 我们还是有两个同样的选择, 重复上面的过程, 在行为准则Q 表中寻找 Q(s2, a1) Q(s2, a2) 的值, 并比较他们的大小, 选取较大的一个. 接着根据 a2 我们到达 s3 并在此重复上面的决策过程. Q learning 的方法也就是这样决策的. 看完决策, 我看在来研究一下这张行为准则 Q 表是通过什么样的方式更改, 提升的.
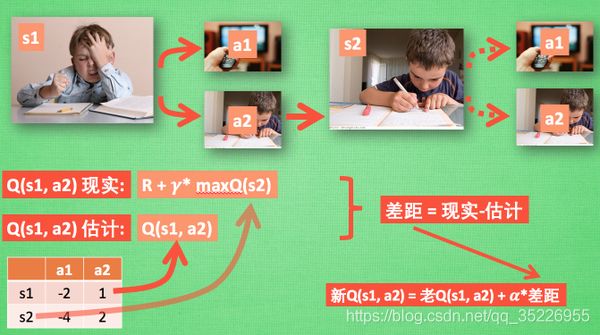
-
QLearning 更新:所以我们回到之前的流程, 根据 Q 表的估计, 因为在 s1 中, a2 的值比较大, 通过之前的决策方法, 我们在 s1 采取了 a2, 并到达 s2, 这时我们开始更新用于决策的 Q 表, 接着我们并没有在实际中采取任何行为, 而是再想象自己在 s2 上采取了每种行为, 分别看看两种行为哪一个的 Q 值大, 比如说 Q(s2, a2) 的值比 Q(s2, a1) 的大, 所以我们把大的 Q(s2, a2) 乘上一个衰减值 gamma (比如是0.9) 并加上到达s2时所获取的奖励 R (这里还没有获取到我们的棒棒糖, 所以奖励为 0), 因为会获取实实在在的奖励 R , 我们将这个作为我现实中 Q(s1, a2) 的值, 但是我们之前是根据 Q 表估计 Q(s1, a2) 的值. 所以有了现实和估计值, 我们就能更新Q(s1, a2) , 根据 估计与现实的差距, 将这个差距乘以一个学习效率 alpha 累加上老的 Q(s1, a2) 的值 变成新的值. 但时刻记住, 我们虽然用 maxQ(s2) 估算了一下 s2 状态, 但还没有在 s2 做出任何的行为, s2 的行为决策要等到更新完了以后再重新另外做. 这就是 off-policy 的 Q learning 是如何决策和学习优化决策的过程.

-
QLearning 整体算法:这一张图概括了我们之前所有的内容. 这也是 Q learning 的算法, 每次更新我们都用到了 Q 现实和 Q 估计, 而且 Q learning 的迷人之处就是 在 Q(s1, a2) 现实 中, 也包含了一个 Q(s2) 的最大估计值, 将对下一步的衰减的最大估计和当前所得到的奖励当成这一步的现实, 很奇妙吧. 最后我们来说说这套算法中一些参数的意义. Epsilon greedy 是用在决策上的一种策略, 比如 epsilon = 0.9 时, 就说明有90% 的情况我会按照 Q 表的最优值选择行为, 10% 的时间使用随机选行为. alpha是学习率, 来决定这次的误差有多少是要被学习的, alpha是一个小于1 的数. gamma 是对未来 reward 的衰减值.
-
整个算法就是一直不断更新 Q table 里的值, 然后再根据新的值来判断要在某个 state 采取怎样的 action. Qlearning 是一个 off-policy 的算法,且是单步更新的 因为里面的 max action 让 Q table 的更新可以不基于正在经历的经验(可以是现在学习着很久以前的经验,甚至是学习他人的经验).

-
QLearning 中的 γ \gamma γ:我们重写一下 Q(s1) 的公式, 将 Q(s2) 拆开, 因为Q(s2)可以像 Q(s1)一样,是关于Q(s3) 的, 所以可以写成这样, 然后以此类推, 不停地这样写下去, 最后就能写成这样, 可以看出Q(s1) 是有关于之后所有的奖励, 但这些奖励正在衰减, 离 s1 越远的状态衰减越严重. 不好理解? 行, 我们想象 Qlearning 的机器人天生近视眼, gamma = 1 时, 机器人有了一副合适的眼镜, 在 s1 看到的 Q 是未来没有任何衰变的奖励, 也就是机器人能清清楚楚地看到之后所有步的全部价值, 但是当 gamma =0, 近视机器人没了眼镜, 只能摸到眼前的 reward, 同样也就只在乎最近的大奖励, 如果 gamma 从 0 变到 1, 眼镜的度数由浅变深, 对远处的价值看得越清楚, 所以机器人渐渐变得有远见, 不仅仅只看眼前的利益, 也为自己的未来着想.
-
过程推导:博客
-
表示t时刻的Q现实=t时刻的reward+ γ \gamma γ*(t+1)时刻的Q现实。而:
- 也就是QLearning 更新中的 r + γ m a x a ′ Q ( s ′ , a ′ ) r+\gamma{max_{a'}Q(s',a')} r+γmaxa′Q(s′,a′),即Q现实(即采取maxQ对应的动作后的结果),而Q(s,a)为Q估计(从Q表中查询的结果),计算两者之间的error,并用来更新Q(s,a),即更新Q表中的这一项。表示的是,在t+1时刻的状态下选择Q值最大的action对应的Q值* γ \gamma γ+t时刻的reward的结果为t时刻的状态下选择action a t a_t at的Q现实值。
(2) Sarsa
- state-action-reward-state-action,简称Sarsa
- on-policy算法
- 在强化学习中 Sarsa 和 Q learning 及其类似, 这节内容会基于之前我们所讲的 Q learning. 所以还不熟悉 Q learning 的朋友们, 请前往我制作的 Q learning 简介 (知乎专栏). 我们会对比 Q learning, 来看看 Sarsa 是特殊在哪些方面. 和上次一样, 我们还是使用写作业和看电视这个例子. 没写完作业去看电视被打, 写完了作业有糖吃.

- Sarsa 决策:Sarsa 的决策部分和 Q learning 一模一样, 因为我们使用的是 Q 表的形式决策, 所以我们会在 Q 表中挑选值较大的动作值施加在环境中来换取奖惩. 但是不同的地方在于 Sarsa 的更新方式是不一样的.
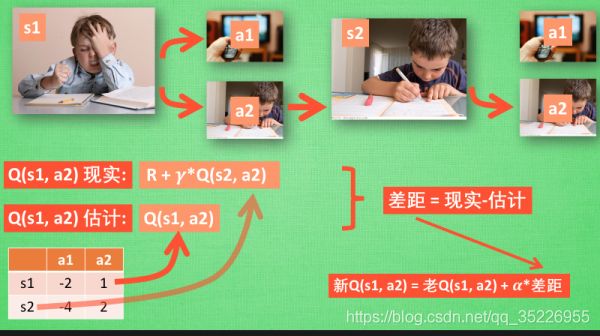
- Sarsa 更新行为准则:同样, 我们会经历正在写作业的状态 s1, 然后再挑选一个带来最大潜在奖励的动作 a2, 这样我们就到达了 继续写作业状态 s2, 而在这一步, 如果你用的是 Q learning, 你会观看一下在 s2 上选取哪一个动作会带来最大的奖励, 但是在真正要做决定时, 却不一定会选取到那个带来最大奖励的动作, Q-learning 在这一步只是估计了一下接下来的动作值. 而 Sarsa 是实践派, 他说到做到, 在 s2 这一步估算的动作也是接下来要做的动作. 所以 Q(s1, a2) 现实的计算值, 我们也会稍稍改动, 去掉maxQ, 取而代之的是在 s2 上我们实实在在选取的 a2 的 Q 值. 最后像 Q learning 一样, 求出现实和估计的差距 并更新 Q 表里的 Q(s1, a2).

- 对比 Sarsa 和 Qlearning 算法:从算法来看, 这就是他们两最大的不同之处了. 因为 Sarsa 是说到做到型, 所以我们也叫他 on-policy, 在线学习, 学着自己在做的事情. 而 Q learning 是说到但并不一定做到, 所以它也叫作 Off-policy, 离线学习. 而因为有了 maxQ, Q-learning 也是一个特别勇敢的算法. 从公式上看,Q-Learning是用什么来更新Q函数呢?是用下一次的action计算得到的Q现实-Q估计,而其下一次的action是怎么决定出来的呢?是假设让Q最大的那个action,但下次state时一定是这个action吗?当然不一定,有可能是随机选择。而Sarsa也是一样用下一次的action计算得到的Q现实-Q估计,但其下一次的action就不是猜想max了,而是真实去行动之后得到的next action(会作为参数传入这个公式进行Q函数的学习)。相当于,SARSA认为实践是检验真理的唯一途径,它真正去走然后拿到下一次的action来更新这一次的state对应的Q函数,而Q-learning是我不要你以为,我要我以为,我以为你是这么走的,那你就是这么走的,那你实际有可能不是maxQ这么走,而是随机走。一句话总结就是:Qlearning是根据假象让下一次Q最大的action来更新这一次的agent,但下一次不一定真的选它指定的那个action(因为还有随机选择action的可能),收集数据的agent和更新的agent不是同一个,因此off-policy;而Sarsa则是先直接根据下一步的state让agent拿到下一次的真实action用以更新agent,且下一步的action就是真实的下一步要走的action,收集数据的agent和更新的agent是同一个,因此on-policy。不过注意:两者根据state选择action是都是二选一,要么根据maxQ选,要么随机选。关于下一步的action,Sarsa提前走过了,知道了到底是maxQ选的还是随机选的,而QLearning则不知道。
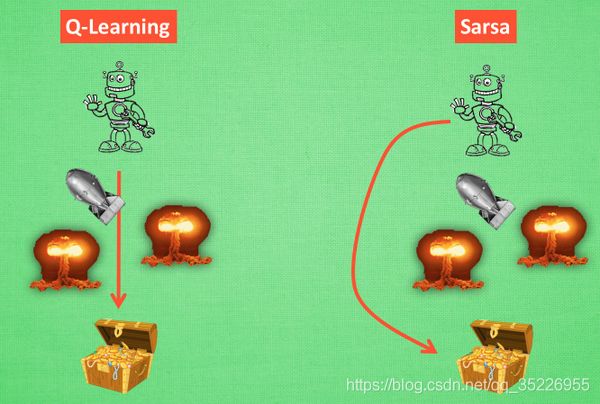
- 为什么说他勇敢呢, 因为 Q learning 机器人 永远都会选择最近的一条通往成功的道路, 不管这条路会有多危险. 而 Sarsa 则是相当保守, 他会选择离危险远远的, 拿到宝藏是次要的, 保住自己的小命才是王道. 这就是使用 Sarsa 方法的不同之处.
- 更详细的对比 Sarsa 和 Qlearning 算法: 区别在于选择action(当前动作和下一个状态采取的动作)的选择。
- Q-learning每次使用 ϵ \epsilon ϵ-greedy的方法(1- ϵ \epsilon ϵ的概率按Q值选, ϵ \epsilon ϵ的概率随机选)选择当前状态的action,而在更新Q(state, action)的时候,是使用Q(next_state, next_acion),其中next_action是使Q(next_state, next_acion)最大的动作。然后state=next_state,动作再重新选择,next_acion值用于更新Q值。
- Sarsa则不同。使用epsilon-greedy选择next_state的next_action,然后用Q(next_state, next_acion)来更新Q(state, action),更新的时候:state=next_state, action=next_action
- 从中就可以看出两个算法的区别,Sarsa是一种on-policy算法,Q-learning是一种off-policy算法。Sarsa选取的是一种保守的策略,他在更新Q值的时候已经为未来规划好了动作,对错误和死亡比较敏感。而Q-learning每次在更新的时候选取的是最大化Q的方向,而当下一个状态时,再重新选择动作,Q-learning是一种鲁莽、大胆、贪婪的算法,对于死亡和错误并不在乎。在实际中,如果你比较在乎机器的损害就用一种保守的算法,在训练时,可以减少机器损害的次数。
- 总结:Sarsa:选择的是一条最安全的道路,远离陷阱;Q-learning:选择的是一条最快的道路,尽快到达出口。
(3) Sarsa( λ \lambda λ)
- Sarsa 是一种单步更新的on-policy算法, 在环境中每走一步, 更新一次自己的行为准则, 我们可以将这种 Sarsa记为 Sarsa(0), 因为他等走完这一步以后直接更新行为准则。如果延续这种想法, 走完两步再更新, 可以记为Sarsa(1)。同理, 如果等待回合完毕我们一次性再更新呢, 比如这回合我们走了 n 步, 那我们就叫 Sarsa(n). 为了统一这样的流程, 我们就有了一个 λ \lambda λ值来代替我们想要选择的步数, 这也就是 Sarsa( λ \lambda λ) 的由来. 我们看看最极端的两个例子, 对比单步更新和回合更新, 看看回合更新的优势在哪里.
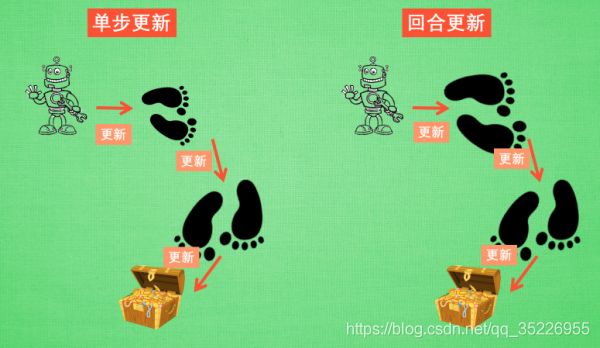
- 单步更新 and 回合更新:虽然我们每一步都在更新, 但是在没有获取宝藏的时候, 我们现在站着的这一步也没有得到任何更新, 也就是直到获取宝藏时, 我们才为获取到宝藏的上一步更新为: 这一步很好, 和获取宝藏是有关联的, 而之前为了获取宝藏所走的所有步都被认为和获取宝藏没关系. 回合更新虽然我要等到这回合结束, 才开始对本回合所经历的所有步都添加更新, 但是这所有的步都是和宝藏有关系的, 都是为了得到宝藏需要学习的步, 所以每一个脚印在下回合被选则的几率又高了一些. 在这种角度来看, 回合更新似乎会有效率一些。
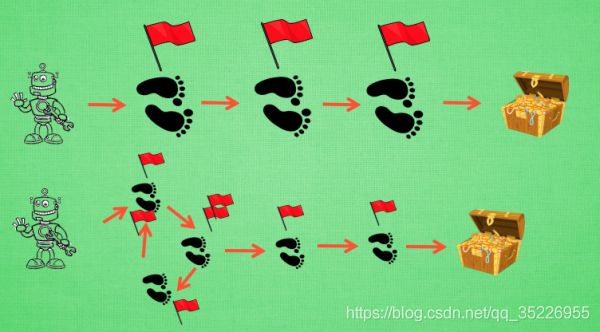
- 有时迷茫:我们看看这种情况, 还是使用单步更新的方法在每一步都进行更新, 但是同时记下之前的寻宝之路. 你可以想像, 每走一步, 插上一个小旗子, 这样我们就能清楚的知道除了最近的一步, 找到宝物时还需要更新哪些步了. 不过, 有时候情况可能没有这么乐观. 开始的几次, 因为完全没有头绪, 我可能在原地打转了很久, 然后才找到宝藏, 那些重复的脚步真的对我拿到宝藏很有必要吗? 答案我们都知道. 所以Sarsa( λ \lambda λ)就来拯救你啦.
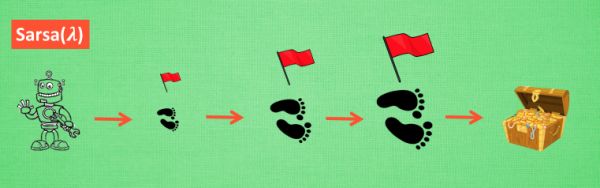
- λ \lambda λ含义:其实 lambda 就是一个衰变值, 他可以让你知道离奖励越远的步可能并不是让你最快拿到奖励的步, 所以我们想象我们站在宝藏的位置, 回头看看我们走过的寻宝之路, 离宝藏越近的脚印越看得清, 远处的脚印太渺小, 我们都很难看清, 那我们就索性记下离宝藏越近的脚印越重要, 越需要被好好的更新. 和之前我们提到过的 奖励衰减值 gamma 一样, lambda 是脚步衰减值, 都是一个在 0 和 1 之间的数.

- λ \lambda λ取值:当 lambda 取0, 就变成了 Sarsa 的单步更新, 当 lambda 取 1, 就变成了回合更新, 对所有步更新的力度都是一样. 当 lambda 在 0 和 1 之间, 取值越大, 离宝藏越近的步更新力度越大. 这样我们就不用受限于单步更新的每次只能更新最近的一步, 我们可以更有效率的更新所有相关步了.
- 总结:Sarsa( λ \lambda λ) 是基于 Sarsa 方法的升级版, 他能更有效率地学习到怎么样获得好的 reward. 如果说 Sarsa 和 Q-Learning 都是每次获取到 reward, 只更新获取到 reward 的前一步. 那 Sarsa( λ \lambda λ)就是更新获取到 reward 的前 λ \lambda λ步, λ ∈ [ 0 , 1 ] \lambda \in [0,1] λ∈[0,1]。如果 λ = 0 \lambda=0 λ=0, Sarsa( λ \lambda λ)就是 Sarsa, 只更新获取到 reward 前经历的最后一步。如果 λ = 1 \lambda=1 λ=1, Sarsa( λ \lambda λ)更新的是 获取到 reward 前所有经历的步。
(4) Deep Q Network (DQN)
- 深度Q网络算法

- 强化学习+神经网络:之前我们所谈论到的强化学习方法都是比较传统的方式, 而如今, 随着机器学习在日常生活中的各种应用, 各种机器学习方法也在融汇, 合并, 升级. 而我们今天所要探讨的强化学习则是这么一种融合了神经网络和 Q learning 的方法, 名字叫做 Deep Q Network. 这种新型结构是为什么被提出来呢? 原来, 传统的表格形式的强化学习有这样一个瓶颈.
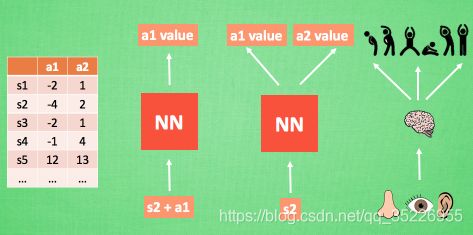
- 神经网络的作用:我们使用表格(Q表)来存储每一个状态 state,和在这个 state 每个行为 action 所拥有的 Q 值. 而当今问题是在太复杂, 状态可以多到比天上的星星还多(比如下围棋). 如果全用表格来存储它们, 恐怕我们的计算机有再大的内存都不够, 而且每次在这么大的表格中搜索对应的状态也是一件很耗时的事. 不过, 在机器学习中, 有一种方法对这种事情很在行, 那就是神经网络. 我们可以将状态和动作当成神经网络的输入, 然后经过神经网络分析后得到动作的 Q 值, 这样我们就没必要在表格中记录 Q 值, 而是直接使用神经网络生成 Q 值. 还有一种形式是这样的, 我们也能只输入状态值, 输出所有的动作值, 然后按照 Q-Learning 的原则, 直接选择拥有最大值的动作当做下一步要做的动作. 我们可以想象, 神经网络接受外部的信息, 相当于眼睛鼻子耳朵收集信息, 然后通过大脑加工输出每种动作的值, 最后通过强化学习的方式选择动作.

- 更新神经网络:接下来我们基于第二种神经网络(仅输入状态)来分析, 我们知道, 神经网络是要被训练才能预测出准确的值. 那在强化学习中, 神经网络是如何被训练的呢? 首先, 我们需要 a1, a2 正确的Q值, 这个 Q 值我们就用之前在 Q learning 中的 Q 现实来代替. 同样我们还需要一个 Q 估计 来实现神经网络的更新. 所以神经网络的的参数就是老的 NN 参数 加学习率 alpha 乘以 Q 现实 和 Q 估计 的差距. 我们整理一下,即:

- 我们通过 NN 预测出Q(s2, a1) 和 Q(s2,a2) 的值, 这就是 Q 估计. 然后我们选取 Q 估计中最大值的动作来换取环境中的奖励 reward. 而 Q 现实中也包含从神经网络分析出来的两个 Q 估计值, 不过这个 Q 估计是针对于下一步在 s’ 的估计. 最后再通过刚刚所说的算法更新神经网络中的参数. 但是这并不是 DQN 会玩电动的根本原因. 还有两大因素支撑着 DQN 使得它变得无比强大. 这两大因素就是 Experience replay 和 Fixed Q-targets.

- DQN 两大利器:简单来说, DQN 有一个记忆库用于学习之前的经历. 在之前的简介影片中提到过, Q learning 是一种 off-policy 离线学习法, 它能学习当前经历着的, 也能学习过去经历过的, 甚至是学习别人的经历. 所以每次 DQN 更新的时候, 我们都可以随机抽取一些之前的经历进行学习. 随机抽取这种做法打乱了经历之间的相关性, 也使得神经网络更新更有效率. Fixed Q-targets 也是一种打乱相关性的机理, 我们就会在 DQN 中使用到两个结构相同但参数不同的神经网络, 预测 Q 估计 的神经网络具备最新的参数(预测这一步状态s下的Q值), 而预测 Q 现实的神经网络使用的参数则是很久以前的(预测下一步状态s’下的Q值). 有了这两种提升手段, DQN 才能在一些游戏中超越人类.
- 算法流程:

(5) Double DQN
- 一句话概括, DQN 基于 Q-Learning, Q-Learning 中有 Qmax, Qmax 会导致 Q现实 当中的过估计 (overestimate). 而 Double DQN 就是用来解决过估计的. 在实际问题中, 如果你输出你的 DQN 的 Q 值, 可能就会发现, Q 值都超级大. 这就是出现了 overestimate.
- 我们知道 DQN 的神经网络部分可以看成一个 最新的神经网络 + 老神经网络, 他们有相同的结构, 但内部的参数更新却有时差. 而它的 Q现实 部分是这样的:
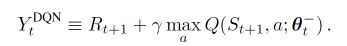
- 因为我们的神经网络预测 Qmax 本来就有误差, 每次也向着最大误差的 Q现实 改进神经网络, 就是因为这个 Qmax 导致了 overestimate. 所以 Double DQN 的想法就是引入另一个神经网络来打消一些最大误差的影响. 而 DQN 中本来就有两个神经网络, 我们何不利用一下这个地理优势呢. 所以, 我们用 Q估计 的神经网络估计 Q现实 中 Qmax(s’, a’) 的最大动作值. 然后用这个被 Q估计 估计出来的动作来选择 Q现实 中的 Q(s’). 总结一下:
- 有两个神经网络: Q_eval (Q估计中的), Q_next (Q现实中的)。原本的 Q_next = max(Q_next(s’, a_all))。Double DQN 中的 Q_next = Q_next(s’, argmax(Q_eval(s’, a_all))). 也可以表达成下面那样:
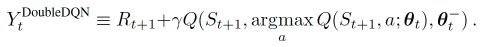
- 总结:Q_next = max(Q_next(s’, a_all))是找出最大的Q,是绝对的,会导致Q越来越大从而造成过估计;而Q_next = Q_next(s’, argmax(Q_eval(s’, a_all)))是随机的,他只在乎在s’下不同动作在Q_eval评估中最大的动作,然后算出在Q_next网络中的Q值,这避免了Q_next网络对应的Q值越来越大,因为对Q_next网络而言始终都是去算s和a对应的值,并不要求max。而Q_eval确实会越来越大,但这不要紧,因为每个C个step,就会把Q_next复制给Q_eval了,刚变大的趋势又从零开始啦~
(6) Prioritized Experience Replay (DQN)
- 先验回放DQN算法
- 比如王者,一局游戏中奖励很稀疏;而有的游戏还会存在正负reward不均衡的现象,比如吃鸡中KD比远远大于1,因此玩家死亡造成的奖励次数远远少于玩家杀人得到的奖励次数。这是就需要Prioritized Experience Replay
- 算法如下所示:

- 啥意思?算法重点就在于 batch 抽样时并不是随机抽样, 而是按照 Memory 中的样本优先级来抽。 所以这能更有效地找到我们需要学习的样本。
- 那么样本的优先级是怎么定的呢? 原来我们可以用到 TD-error, 也就是 Q现实 - Q估计 来规定优先学习的程度. 如果 TD-error 越大, 就代表我们的预测精度还有很多上升空间, 那么这个样本就越需要被学习, 也就是优先级 p 越高.
- 有了 TD-error 就有了优先级 p, 那我们如何有效地根据 p 来抽样呢? 如果每次抽样都需要针对 p 对所有样本排序, 这将会是一件非常消耗计算能力的事. 好在我们还有其他方法, 这种方法不会对得到的样本进行排序. 这就是这篇 paper 中提到的 SumTree.
- SumTree 是一种树形结构, 每片树叶存储每个样本的优先级 p, 每个树枝节点只有两个分叉, 节点的值是两个分叉的和, 所以 SumTree 的顶端就是所有 p 的和. 如下图所示, 最下面一层树叶存储样本的 p, 叶子上一层最左边的 13 = 3 + 10, 按这个规律相加, 顶层的 root 就是全部 p 的和了.
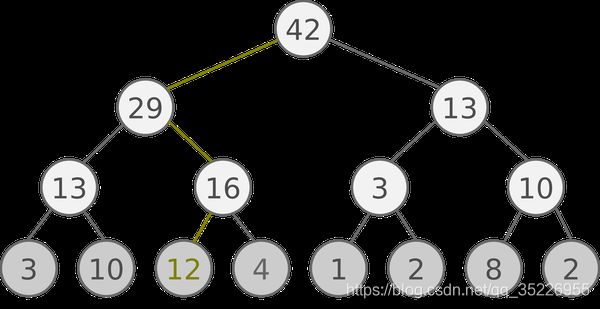
- 抽样时, 我们会将 p 的总和除以 batch size, 分成 batch size 那么多区间, (n=sum§/batch_size). 如果将所有 node 的 priority 加起来是42的话, 我们如果抽6个样本, 这时的区间拥有的 priority 可能是这样:[0-7), [7-14), [14-21), [21-28), [28-35), [35-42]
- 然后在每个区间里随机选取一个数. 比如在区间[21-28)里选到了24, 就按照这个 24 从最顶上的42开始向下搜索. 首先看到最顶上 42 下面有两个 child nodes, 拿着手中的24对比左边的 child 29, 如果 左边的 child 比自己手中的值大, 那我们就走左边这条路, 接着再对比 29 下面的左边那个点 13, 这时, 手中的 24 比 13 大, 那我们就走右边的路, 并且将手中的值根据 13 修改一下, 变成 24-13 = 11. 接着拿着 11 和 13 左下角的 12 比, 结果 12 比 11 大, 那我们就选 12 当做这次选到的 priority, 并且也选择 12 对应的数据.
(7) Dueling DQN
- 决斗DQN算法
- 只要稍稍修改 DQN 中神经网络的结构, 就能大幅提升学习效果, 加速收敛. 这种新方法叫做 Dueling DQN(我们发现当可用动作越高, 学习难度就越大, 不过 Dueling DQN 还是会比 Natural DQN 学习得更快. 收敛效果更好.). 用一句话来概括 Dueling DQN 就是:它将每个动作的 Q 拆分成了 state 的 Value 加上 每个动作的 Advantage.
- Dueling 算法:

- 图中上面是一般的 DQN 的 Q值 神经网络. 下面就是 Dueling DQN 中的 Q值 神经网络了. 那具体是哪里不同了呢?下面这个公式解释了不同之处. 原来 DQN 神经网络直接输出的是每种动作的 Q值, 而 Dueling DQN 每个动作的 Q值 是有下面的公式确定的:
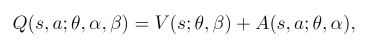
- 它分成了这个 state 的值, 加上每个动作在这个 state 上的 advantage. 因为有时候在某种 state, 无论做什么动作, 对下一个 state 都没有多大影响. 比如 paper 中的这张图:
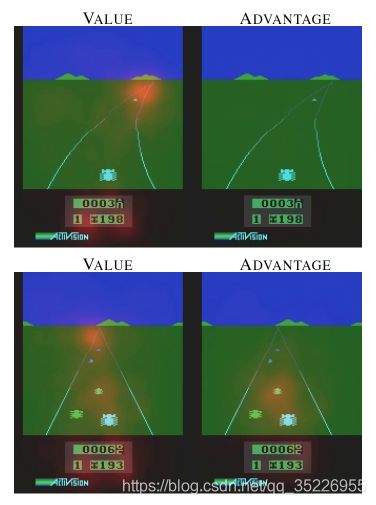
- 这是开车的游戏, 左边是 state value, 发红的部分证明了 state value 和前面的路线有关, 右边是 advantage, 发红的部分说明了 advantage 很在乎旁边要靠近的车子, 这时的动作会受更多 advantage 的影响. 发红的地方左右了自己车子的移动原则.
2.2.2 Policy-Based算法
(1) Vanilla Policy Gradient (VPG)
- 和以往的强化学习方法不同:强化学习是一个通过奖惩来学习正确行为的机制. 家族中有很多种不一样的成员, 有学习奖惩值, 根据自己认为的高价值选行为, 比如 Q learning, Deep Q Network, 也有不通过分析奖励值, 直接输出行为的方法, 这就是今天要说的 Policy Gradients 了. 甚至我们可以为 Policy Gradients 加上一个神经网络来输出预测的动作. 对比起以值为基础的方法, Policy Gradients 直接输出动作的最大好处就是, 它能在一个连续区间内挑选动作, 而基于值的, 比如 Q-learning, 它如果在无穷多的动作中计算价值, 从而选择行为, 这, 它可吃不消。
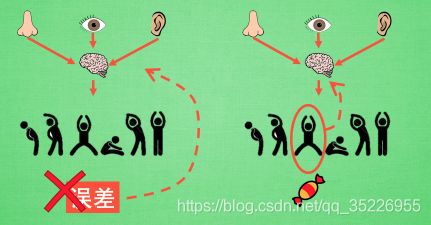
- 更新不同之处:有了神经网络当然方便, 但是, 我们怎么进行神经网络的误差反向传递呢? Policy Gradients 的误差又是什么呢? 答案是! 哈哈, 没有误差! 但是他的确是在进行某一种的反向传递. 这种反向传递的目的是让这次被选中的行为更有可能在下次发生. 但是我们要怎么确定这个行为是不是应当被增加被选的概率呢? 这时候我们的老朋友, reward 奖惩正可以在这时候派上用场。
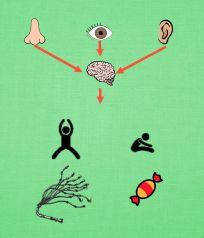
- 具体更新步骤:现在我们来演示一遍, 观测的信息通过神经网络分析, 选出了左边的行为, 我们直接进行反向传递, 使之下次被选的可能性增加, 但是奖惩信息却告诉我们, 这次的行为是不好的, 那我们的动作可能性增加的幅度 随之被减低. 这样就能靠奖励来左右我们的神经网络反向传递. 我们再来举个例子, 假如这次的观测信息让神经网络选择了右边的行为, 右边的行为随之想要进行反向传递, 使右边的行为下次被多选一点, 这时, 奖惩信息也来了, 告诉我们这是好行为, 那我们就在这次反向传递的时候加大力度, 让它下次被多选的幅度更猛烈! 这就是 Policy Gradients 的核心思想了. 很简单吧.
- Policy gradient 是 RL 中另外一个大家族, 他不像 Value-based 方法 (Q learning, Sarsa), 但他也要接受环境信息 (observation), 不同的是他要输出不是 action 的 value, 而是具体的那一个 action, 这样 policy gradient 就跳过了 value 这个阶段. 而且个人认为 Policy gradient 最大的一个优势是: 输出的这个 action 可以是一个连续的值, 之前我们说到的 value-based 方法输出的都是不连续的值, 然后再选择值最大的 action. 而 policy gradient 可以在一个连续分布上选取 action.
- 算法:VPG是一种基于回合更新的方法(一个episode结束才更新),算法流程如下:

- delta(log(Policy(s,a))*V) 表示在 状态 s 对所选动作 a 的吃惊度, 如果 Policy(s,a) 概率越小, 反向的 log(Policy(s,a)) (即 -log§) 反而越大. 如果在 Policy(s,a) 很小的情况下, 拿到了一个 大的 R, 也就是 大的 V, 那 -delta(log(Policy(s, a))*V) 就更大, 表示更吃惊, (我选了一个不常选的动作, 却发现原来它能得到了一个好的 reward, 那我就得对我这次的参数进行一个大幅修改). 这就是吃惊度的物理意义啦.
- 其中红色方框部分的是更新参数 θ \theta θ所用到的梯度信息(最终化简结果),下面利用数学公式去推导它!
- 前面已经导出了
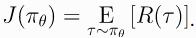
- 那么梯度下降法中时怎么利用 J ( π ) J(\pi) J(π)的梯度信息更新参数的呢?如下:
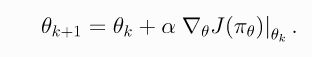
- 其中 α \alpha α是学习率,那么关键问题就是如何计算梯度 ▽ θ J θ ( π θ ) ∣ θ k \triangledown_{\theta}J_{\theta}(\pi_{\theta})|_{\theta_k} ▽θJθ(πθ)∣θk,咋算呢?
- 由于前面已经给出了得到最终轨迹 τ \tau τ的概率为:
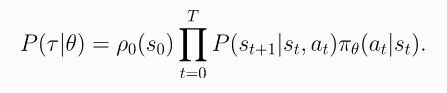
- 那么根据对数导数公式 ▽ l o g f ( x ) ▽ f ( x ) = 1 f ( x ) \frac{\triangledown{logf(x)}}{\triangledown{f(x)}}=\frac{1}{f(x)} ▽f(x)▽logf(x)=f(x)1 导出 ▽ f ( x ) = f ( x ) ▽ l o g f ( x ) \triangledown{f(x)}=f(x)\triangledown{logf(x)} ▽f(x)=f(x)▽logf(x),上式有:
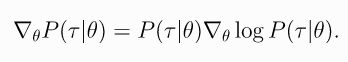
- 然后根据对数的运算规则将最终轨迹 τ \tau τ的概率的 l o g log log进行展开,得到:

- 其中,有一些项和 θ \theta θ无关,求导后结果为0,分别是如下几项:

- 那么可以对 l o g P ( τ ∣ θ ) logP(\tau|\theta) logP(τ∣θ)求导并化简可以得到:

- 从头到尾的过程也就是:

- 而agent和环境交互 N N N次得到的轨迹 D = { τ i } i = 1 , . . . , N D=\{\tau_i\}_{i=1,...,N} D={τi}i=1,...,N下的梯度 ▽ θ J ( π θ ) \triangledown_{\theta}{J(\pi_\theta)} ▽θJ(πθ)可以近似表示为(期望是无数次的平均值,因此 N N N次的结果只能是近似):

- 也就是说,agent和环境交互 N N N次得到的轨迹 D = { τ i } i = 1 , . . . , N D=\{\tau_i\}_{i=1,...,N} D={τi}i=1,...,N下参数更新公式从前面的 θ k + 1 = θ k + α ⋅ ▽ θ J θ ( π θ ) ∣ θ k \theta_{k+1}=\theta_{k}+{\alpha}{\cdot}{\triangledown_{\theta}J_{\theta}(\pi_{\theta})|_{\theta_k}} θk+1=θk+α⋅▽θJθ(πθ)∣θk特殊化为: θ k + 1 = θ k + α ⋅ g ^ \theta_{k+1}=\theta_{k}+{\alpha}{\cdot}{\hat{g}} θk+1=θk+α⋅g^
- 而这个 g ^ \hat{g} g^也就是前面算法部分提到的红色方框部分的内容。
- 代码实现:
""" 1. Making the Policy Network. """ # make core of policy network logits_net = mlp(sizes=[obs_dim]+hidden_sizes+[n_acts]) # make function to compute action distribution def get_policy(obs): logits = logits_net(obs) return Categorical(logits=logits) # make action selection function (outputs int actions, sampled from policy) def get_action(obs): return get_policy(obs).sample().item() """ 2. Making the Loss Function. """ # make loss function whose gradient, for the right data, is policy gradient def compute_loss(obs, act, weights): logp = get_policy(obs).log_prob(act) return -(logp * weights).mean() """ 3. Running One Epoch of Training. """ # for training policy def train_one_epoch(): # make some empty lists for logging. batch_obs = [] # for observations batch_acts = [] # for actions batch_weights = [] # for R(tau) weighting in policy gradient batch_rets = [] # for measuring episode returns batch_lens = [] # for measuring episode lengths # reset episode-specific variables obs = env.reset() # first obs comes from starting distribution done = False # signal from environment that episode is over ep_rews = [] # list for rewards accrued throughout ep # render first episode of each epoch finished_rendering_this_epoch = False # collect experience by acting in the environment with current policy while True: # rendering if (not finished_rendering_this_epoch) and render: env.render() # save obs batch_obs.append(obs.copy()) # act in the environment act = get_action(torch.as_tensor(obs, dtype=torch.float32)) obs, rew, done, _ = env.step(act) # save action, reward batch_acts.append(act) ep_rews.append(rew) if done: # if episode is over, record info about episode ep_ret, ep_len = sum(ep_rews), len(ep_rews) # ep_ret即整个episode的reward之和,回合更新(一个episode之后才更新policy) batch_rets.append(ep_ret) batch_lens.append(ep_len) # the weight for each logprob(a|s) is R(tau) batch_weights += [ep_ret] * ep_len # reset episode-specific variables obs, done, ep_rews = env.reset(), False, [] # won't render again this epoch finished_rendering_this_epoch = True # end experience loop if we have enough of it if len(batch_obs) > batch_size: break # take a single policy gradient update step optimizer.zero_grad() batch_loss = compute_loss(obs=torch.as_tensor(batch_obs, dtype=torch.float32), act=torch.as_tensor(batch_acts, dtype=torch.int32), weights=torch.as_tensor(batch_weights, dtype=torch.float32) ) batch_loss.backward() optimizer.step() return batch_loss, batch_rets, batch_lens - 还能在算法中进行哪些改进呢?上面最终得到的形式是:
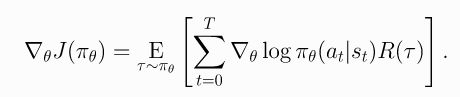
- 而其中的Return还可以根据2.2.1中的 R ( τ ) = ∑ t = 0 T r t R(\tau)=\sum_{t=0}^{T}{r_t} R(τ)=∑t=0Trt展开为一个episode中每个step的reward的组合(当然,也可以按照 R ( τ ) = ∑ t = 0 ∞ γ t r t R(\tau)=\sum_{t=0}^{\infty}{{\gamma^t}{r_t}} R(τ)=∑t=0∞γtrt的无限有折扣形式,这里取有限无折扣形式,那么得到:

- 即这个episode所有reward之和对采取的action a t a_t at的log的梯度进行加权。然而,这是不合理的!Spining Up的说法是
Taking a step with this gradient pushes up the log-probabilities of each action in proportion to R(\tau), the sum of all rewards ever obtained. But this doesn’t make much sense. Agents should really only reinforce actions on the basis of their consequences. Rewards obtained before taking an action have no bearing on how good that action was: only rewards that come after.,也就是说,没必要算整个episode的reward,每个action都会获得一个reward,而采取这个action a t a_t at之前的reward采取现在这个action a t a_t at的好坏无关,而之后的reward都与这个action a t a_t at有关(直到这个episode截止),于是修改上式为:
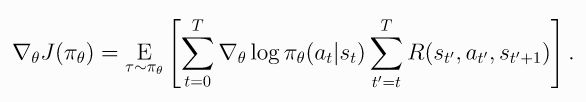
- 即action a t a_t at是用来加权的rewad只是用 t t t时刻之后的reward来加权。
- 其中:
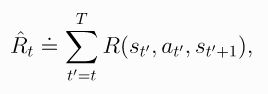
- 以上叫做Don’t Let the Past Distract You,也被称为reward-to-go形式。代码实现如下:
# 增加 def reward_to_go(rews): n = len(rews) rtgs = np.zeros_like(rews) for i in reversed(range(n)): # 现在只计算t时刻之后的reward之和给a_t进行加权了 rtgs[i] = rews[i] + (rtgs[i+1] if i+1 < n else 0) return rtgs # 上面代码块中68-69行的: """ # the weight for each logprob(a|s) is R(tau) batch_weights += [ep_ret] * ep_len """ # 替换为: # the weight for each logprob(a_t|s_t) is reward-to-go from t batch_weights += list(reward_to_go(ep_rews)) - 还可以改进吗?Add a Baseline!啥意思,也就是说加一个baseline结果,让做出的action的 R t ^ \hat{R_t} Rt^大于这个basline才在下一次遇到相同情况下增加做这个action a t a_t at的概率;否则就减小做这个action a t a_t at的概率。形式如下:
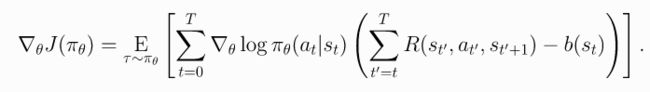
- 其中 b ( s t ) b(s_t) b(st)就是所说的baseline,是一个仅依赖与状态state的函数。用的最多的就是选择on-policy value function V π ( s t ) V^{\pi}(s_t) Vπ(st), 即选择 b ( s t ) = V π ( s t ) b(s_t)=V^{\pi}(s_t) b(st)=Vπ(st)。也就是说agent在做出action a t a_t at后根据平均回报( V π ( s t ) V^{\pi}(s_t) Vπ(st))行事。而选择 V π ( s t ) V^{\pi}(s_t) Vπ(st)具有减少策略梯度样本估计方差的理想效果, 这导致更快、更稳定的policy学习。 从概念的角度来看:它编码了一种直觉,即如果agent得到了它的预期,它应该“感觉”中立,照着这个中立的感觉行事。
- 上面说到一般选择 b ( s t ) = V π ( s t ) b(s_t)=V^{\pi}(s_t) b(st)=Vπ(st),那 V π ( s t ) V^{\pi}(s_t) Vπ(st)很难精确计算呀!咋办?近似计算呗!通过一个神经网络 V ϕ V_{\phi} Vϕ来算,这个 V ϕ V_{\phi} Vϕ网络和policy网络同时更新,以便价值网络始终接近最新策略的价值函数。在大多数策略优化算法(包括 VPG、TRPO、PPO 和 A2C)实现中,使用的学习 V ϕ V_{\phi} Vϕ网络的最简单方法是最小化 V π ( s t ) V^{\pi}(s_t) Vπ(st)和 R t ^ \hat{R_t} Rt^的均方误差:

- 最终得到的 ϕ k \phi_k ϕk就是估算 V π ( s t ) V^{\pi}(s_t) Vπ(st)的 V ϕ V_{\phi} Vϕ网络的参数。
- 那还有一个问题就是,为啥可以这个肆意的在梯度公式中增加一项 b ( s t ) b(s_t) b(st)呢?那是因为Expected Grad-Log-Prob (EGLP)定理,即:

- 即对于任何仅依赖于状态的函数 b,总有:

- 因此可以加这么个 b ( s t ) b(s_t) b(st)项到梯度中。
- 更一般地(总结上面三种形式:普通reward、reward2go、baseline),Reward的期望的梯度 ▽ θ J ( π θ ) \triangledown_{\theta}J(\pi_\theta) ▽θJ(πθ)可以写成如下形式:
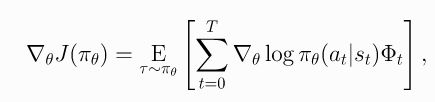
- 其中,

- 尽管上面三种形式有不同的方差,但都会导致policy的梯度的期望值相同。不过,还有两种形式,分别是On-Policy Action-Value Function:
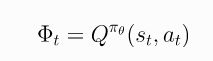
- 和The Advantage Function:

- 其中:
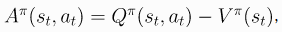
- 证明略过,同样有相同的期望。
- 注意:以上五种形式在其他Policy Optimization算法中同样可以使用,后面就不赘述了!
- 复习一下:
- VPG是on-policy算法,支持离散和连续的动作空间
- 算法如下:

2.2.3 Value-Based+Policy-Based算法
(1) Actor Critic
- Actor Critic是一种on-policy算法,用于具有离散和连续动作空间。
- Actor Critic (演员评判家)合并了 value-based (比如 Q learning) 和 以动作概率(即策略,policy-based)为基础 (比如 Policy Gradients) 两类强化学习算法.

- 为什么要有 Actor 和 Critic:我们有了像 Q-learning 这么伟大的算法, 为什么还要瞎折腾出一个 Actor-Critic? 原来 Actor-Critic 的 Actor 的前生是 Policy Gradients, 这能让它毫不费力地在连续动作中选取合适的动作, 而 Q-learning 做这件事会瘫痪. 那为什么不直接用 Policy Gradients 呢? 原来 Actor Critic 中的 Critic 的前生是 Q-learning 或者其他的 value-based方法 , 能进行单步更新, 而传统的 Policy Gradients 则是回合更新, 这降低了学习效率.

- Actor 和 Critic:现在我们有两套不同的体系, Actor 和 Critic, 他们都能用不同的神经网络来代替 . 结合了 Policy Gradient (Actor) 和 Function Approximation (Critic) 的方法. Actor 基于概率选行为, Critic 基于 Actor 的行为评判行为的得分, Actor 根据 Critic 的评分修改选行为的概率.
- . Actor Critic 方法的优势:可以进行单步更新, 比传统的 Policy Gradient 要快.
- Actor Critic 方法的劣势:取决于 Critic 的价值判断, 但是 Critic 难收敛, 再加上 Actor 的更新, 就更难收敛. 为了解决收敛问题, Google Deepmind 提出了 Actor Critic 升级版 Deep Deterministic Policy Gradient. 后者融合了 DQN 的优势, 解决了收敛难的问题. 我们之后也会要讲到 Deep Deterministic Policy Gradient.
(2) Trust Region Policy Optimization (TRPO)
-
信任区域策略优化算法
-
TRPO是on-policy算法,支持离散和连续的动作空间
-
而根据贝尔曼方程,其实 J ( π ) J(\pi) J(π)可以等价下面的几个替代,即 V π ( s ) V^\pi(s) Vπ(s)、 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)和 A π ( s , a ) A^\pi(s,a) Aπ(s,a)之一均可:
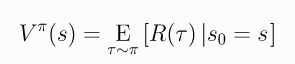
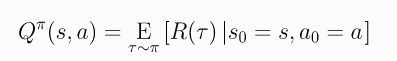
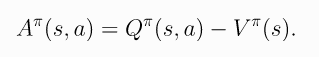
-
L ( θ k , θ ) L(\theta_k, \theta) L(θk,θ)叫做surrogate advantage(替代优势函数),而 π θ k \pi_{\theta_k} πθk和 π θ \pi_\theta πθ分别表示老的policy和当前policy,而 δ \delta δ是很小的一个数。
-
Why可以替换成这样?
-
因为在 D K L ( θ ∣ ∣ θ k ) D_{KL}(\theta||\theta_k) DKL(θ∣∣θk)很小的情况下,表示 π θ k \pi_{\theta_k} πθk和 π θ \pi_\theta πθ网络的输出结果分布近似相同,即 π θ k \pi_{\theta_k} πθk和 π θ \pi_\theta πθ近似相同,因此:

-
即正常形式。因此可以做之前TRPO那样的近似。
-
推导过程为:
-
其中, θ ′ \theta' θ′就是先前的 θ k \theta_k θk,它们具有相近似的表现形式,即 D K L ( θ ∣ ∣ θ k ) D_{KL}(\theta||\theta_k) DKL(θ∣∣θk)很小。
-
因此,能直接将 A θ ( s t , a t ) A^{\theta}(s_t,a_t) Aθ(st,at)替换为 A θ ′ ( s t , a t ) A^{\theta'}(s_t,a_t) Aθ′(st,at);而 P θ ( s t , a t ) = P θ ( a t ∣ s t ) ∗ p θ ( s t ) P_{\theta}(s_t,a_t)=P_{\theta}(a_t|s_t)*p_\theta{(s_t)} Pθ(st,at)=Pθ(at∣st)∗pθ(st)是条件概率公式展开得到的, P θ ′ ( s t , a t ) = P θ ′ ( a t ∣ s t ) ∗ p θ ′ ( s t ) P_{\theta'}(s_t,a_t)=P_{\theta'}(a_t|s_t)*p_\theta'{(s_t)} Pθ′(st,at)=Pθ′(at∣st)∗pθ′(st)同理。而能将 p θ ( s t ) p θ ′ ( s t ) \frac{p_\theta(s_t)}{p_\theta'{(s_t)}} pθ′(st)pθ(st)去掉是因为下面几条:

-
而将 A θ ( s t , a t ) A^{\theta}(s_t,a_t) Aθ(st,at)替换为 A θ ′ ( s t , a t ) A^{\theta'}(s_t,a_t) Aθ′(st,at)就表示现在度量用的老的policy θ ′ \theta' θ′了,即和环境交互的policy,而更新的是policy θ \theta θ,也就是说和环境交互的policy和用于更新的policy不是同一个,也就说明从on-policy变成了off-policy。即:

-
不过,由于 θ ′ \theta' θ′和 θ \theta θ都是同一个网络在不同step的参数,差距也不大,近似认为是on-policy也是合理的。
-
从最终梯度结果,再根据 ▽ f ( x ) = f ( x ) ▽ l o g f ( x ) \triangledown{f(x)}=f(x)\triangledown{logf(x)} ▽f(x)=f(x)▽logf(x),我们可以反推原目标函数为:
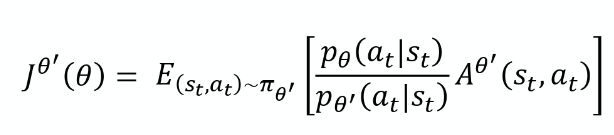
-
其中: p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) \frac{p_\theta(a_t|s_t)}{p_{\theta'}(a_t|s_t)} pθ′(at∣st)pθ(at∣st)也就是所谓的Importance Sampling的weight。即非要用策略P抽样出来的数据,来更新策略Q也不是不可以,乘以一个重要性权重即可。
-
因此,也就导出了最开始的那个式子。
-
而不要忘记了这一切是有条件的,即 D K L ( θ ∣ ∣ θ k ) D_{KL}(\theta||\theta_k) DKL(θ∣∣θk)很小。
-
注意: D K L ( θ ∣ ∣ θ k ) D_{KL}(\theta||\theta_k) DKL(θ∣∣θk)是通过计算两个policy的表现来衡量的,而不是真的把参数拉出来算KL散度,也就是:
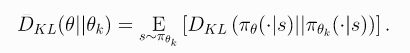
-
即:

-
那现在很明朗了,所谓
信任区域策略优化中信任区域也就是满足 D K L ( θ ∣ ∣ θ k ) D_{KL}(\theta||\theta_k) DKL(θ∣∣θk)的区域了。 -
那有什么优势呢?
-
当然是比VPG更好的效果,更快的收敛啦!
-
其中 g g g是surrogate advantage函数 L ( θ k , θ ) L(\theta_k,\theta) L(θk,θ)对于 θ \theta θ的导数,而 H H H是样本平均KL散度的Hessian值。于是得到:
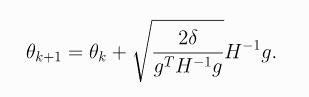
-
上面结果存在一定误差,可以引入线性回溯搜索(a backtracking line search)来修正,得到:
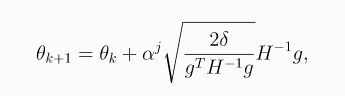
-
其中 α ∈ ( 0 , 1 ) \alpha \in (0,1) α∈(0,1)是回溯系数,而 j j j是使得 π θ k + 1 \pi_{\theta_{k+1}} πθk+1满足KL约束且surrogate advantage函数 L ( θ k , θ ) L(\theta_k,\theta) L(θk,θ)为正的最小非负整数。而由于计算和存储 H − 1 H^{-1} H−1很难,因此可以转换为存储 H x Hx Hx即 g g g,也就是 H x = g Hx=g Hx=g,即:

(3) Proximal Policy Optimization(PPO)
- 近端策略优化
- TRPO是on-policy算法,支持离散和连续的动作空间
- 推导过程和TRPO一样,就是基于TRPO改进的。
- TRPO最终得到:

- 然而:
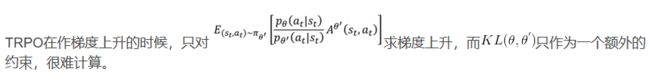
- 于是PPO将KL约束直接做到式子里面,变成:

- 其中:

- PPO和TRPO的区别:

- 上面的PPO算法叫做
Penalty算法,一般叫PPO,而PPO还有一个改进版本PPO-clip,或者叫PPO2:

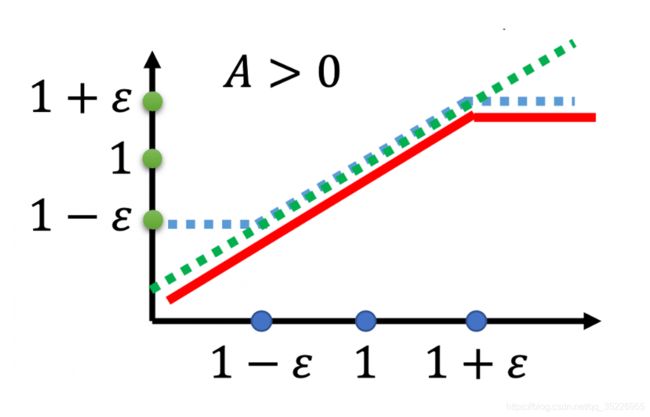
- 其实上就是一个min(a,b),其中a就是普通的TRPO和PPO的前半部分,而b则是一个clip,用来替代KL散度计算部分。其中 ε \varepsilon ε是一个超参数,你要 tune 的,你可以设成 0.1 或 0.2 。
- 我们先看看下面这项这个算出来到底是什么东西:

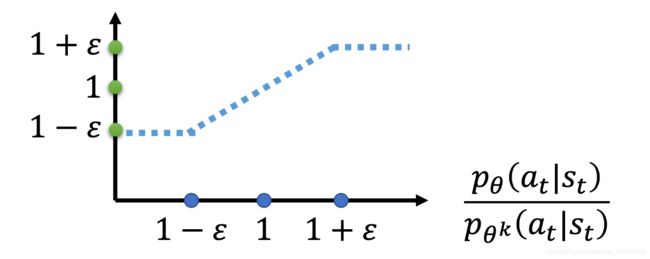


- 其实做了这么多,也就是想要横轴指代的内容:

- 大不要大过1太多,超过 1 + ε 1+\varepsilon 1+ε就截断,小不要小过1太多,低于 1 − ε 1-\varepsilon 1−ε就截断。啥意思?分子分母不要差的太多,也就是KL散度不要太大。
- 最终:

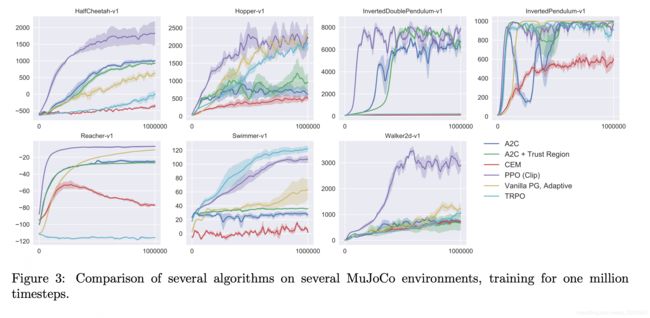
- 性能对比:
- 算法流程:

github仓库
github文档
CSDN博客
代码实现请参考:spining up RL 或 openai RL baseline 或 仓库1 或 仓库2 或 博客
(4) Deep Deterministic Policy Gradient(DDPG)
-
深度确定性策略优化算法
-
DDPG 是一种off-policy算法, 只能用于具有连续动作空间的环境,可以被认为是针对连续动作空间的deep Q-Learning。
-
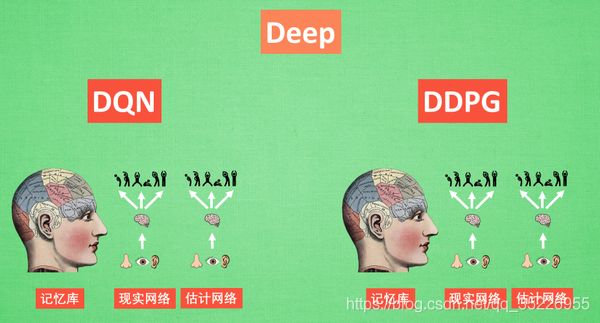
拆分细讲:它吸收了 Actor-Critic 让 Policy gradient 单步更新的精华, 而且还吸收让计算机学会玩游戏的 DQN 的精华, 合并成了一种新算法, 叫做 Deep Deterministic Policy Gradient. 那 DDPG 到底是什么样的算法呢, 我们就拆开来分析, 我们将 DDPG 分成 ‘Deep’ 和 ‘Deterministic Policy Gradient’, 然后 ‘Deterministic Policy Gradient’ 又能被细分为 ‘Deterministic’ 和 ‘Policy Gradient’, 而Deterministic是value-based, Policy Gradient这是policy-based,因此本质是改进的Actor-Critic。接下来, 我们就开始一个个分析啦.
-
Deep 和 DQN:Deep 顾名思义, 就是走向更深层次, 我们在 DQN 的影片当中提到过, 使用一个记忆库和两套结构相同, 但参数更新频率不同的神经网络能有效促进学习. 那我们也把这种思想运用到 DDPG 当中, 使 DDPG 也具备这种优良形式. 但是 DDPG 的神经网络形式却比 DQN 的要复杂一点点.

-
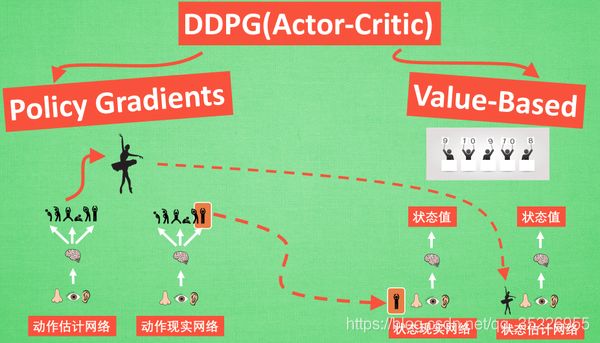
Deterministic Policy Gradient:Policy gradient 我们也在之前的短片中提到过, 相比其他的强化学习方法, 它能被用来在连续动作上进行动作的筛选 . 而且筛选的时候是根据所学习到的动作分布随机进行筛选, 而 Deterministic 有点看不下去, Deterministic 说: 我说兄弟, 你其实在做动作的时候没必要那么不确定, 那么犹豫嘛, 反正你最终都只是要输出一个动作值, 干嘛要随机, 铁定一点, 有什么不好(确定性策略是和随机策略相对而言的,对于某一些动作集合来说,它可能是连续值,或者非常高维的离散值,这样动作的空间维度极大。如果我们使用随机策略,即像DQN一样研究它所有的可能动作的概率,并计算各个可能的动作的价值的话,那需要的样本量是非常大才可行的[每个动作的value要送给critic去算,概率分布上每一点要送给critic算一次,计算量当然大]。于是有人就想出使用确定性策略来简化这个问题。作为随机策略,在相同的策略,在同一个状态处,采用的动作是基于一个概率分布的,即是不确定的。而确定性策略则决定简单点,虽然在同一个状态处,采用的动作概率不同,但是最大概率只有一个,如果我们只取最大概率的动作,去掉这个概率分布,那么就简单多了。即作为确定性策略,相同的策略,在同一个状态处,动作是唯一确定的)。 所以 Deterministic 就改变了输出动作的过程, 斩钉截铁的只在连续动作上输出一个动作值。
-
DDPG 神经网络:现在我们来说说 DDPG 中所用到的神经网络. 它其实和我们之前提到的 Actor-Critic 形式差不多, 也需要有基于 策略 Policy 的神经网络 和基于 价值 Value 的神经网络, 但是为了体现 DQN 的思想, 每种神经网络我们都需要再细分为两个, Policy Gradient 这边, 我们有估计网络和现实网络, 估计网络用来输出实时的动作, 供 actor 在现实中实行. 而现实网络则是用来更新价值网络系统的. 所以我们再来看看价值系统这边, 我们也有现实网络和估计网络, 他们都在输出这个状态的价值, 而输入端却有不同, 状态现实网络这边会拿着从动作现实网络来的动作加上状态的观测值加以分析, 而状态估计网络则是拿着当时 Actor 施加的动作当做输入.在实际运用中, DDPG 的这种做法的确带来了更有效的学习过程.
-
一句话概括 DDPG:Google DeepMind 提出的一种使用 Actor Critic 结构, 但是输出的不是行为的概率, 而是具体的行为, 用于连续动作 (continuous action) 的预测. DDPG 结合了之前获得成功的 DQN 结构, 提高了 Actor Critic 的稳定性和收敛性.
-
关于 Actor 部分, 他的参数更新同样会涉及到 Critic。它的前半部分 grad[Q] 是从 Critic 来的, 这是在说: 这次 Actor 的动作要怎么移动, 才能获得更大的 Q, 而后半部分 grad[u] 是从 Actor 来的, 这是在说: Actor 要怎么样修改自身参数, 使得 Actor 更有可能做这个动作. 所以两者合起来就是在说: Actor 要朝着更有可能获取大 Q 的方向修改动作参数了.
-
它借鉴了 DQN 和 Double Q learning 的方式, 有两个计算 Q 的神经网络, Q_target 中依据下一状态, 用 Actor 来选择动作, 而这时的 Actor 也是一个 Actor_target (有着 Actor 很久之前的参数). 使用这种方法获得的 Q_target 能像 DQN 那样切断相关性, 提高收敛性.
-
其中,如果s’是终止状态(episode结束),则d=1,否则d=0;
-
然后由于DDPG包含DQN,因此还可以直接使用DQN 的两大利器,Experience replay 和 fixed Q-targets。对于后者,就可以得到:

-
其中: μ θ t a r g \mu_{\theta_{targ}} μθtarg就是target policy。
(5) Twin Delayed DDPG (TD3)
-
双延迟DDPG算法。
-
TD3 是一种off-policy算法,只能用于具有连续动作空间的环境。
-
由于DDPG本质是DQN+Policy Gradient,所以DQN的缺点特也有,啥缺点呢?过估计,即 Qmax 会导致 Q现实 当中的过估计 (overestimate)。而之前Value-Based方法中是将DDPG改进为 Double DQN 来解决的。这里不例外,包括了三个trick:
-
第一个trick便是Clipped Double-Q Learning。本质就是Double DQN解决的问题,不过注意,做法不一样。而是学习两个 Q 函数,也就是
Twin,他们都学习一个目标,即两者Q值之间的较小者计算得到:
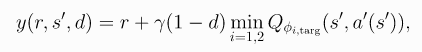
-
第二个trick是 “Delayed” Policy Updates:TD3更新policy(和目标网络)的频率低于Q函数。原文建议每更新Q函数两次才更新一次policy(即actor)。
-
第三个trick是Target Policy Smoothing:TD3给目标动作增加了噪声,使策略更难通过平滑动作变化来利用Q函数的误差信息。具体地如下:
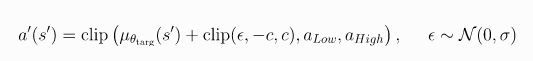
-
Target Policy Smoothing本质上是起到正则的作用。它解决了 DDPG 中可能发生的特定故障模式:如果 Q 函数逼近器针对某些操作产生了不正确的尖峰,则policy将快速利用该尖峰,然后出现脆弱或不正确的行为。Target Policy Smoothing则是通过在动作上平滑 Q 函数来避免这个问题。
-
这三个技巧大大提高了 DDPG 的性能,结果远高于DDPG baseline。
(6) Soft Actor-Critic (SAC)
- 软AC算法
- SAC 是一种off-policy算法,一般只能用于具有连续动作空间的环境。而SAC 的一个替代版本,稍微改变了策略更新规则,可以用来处理离散的动作空间。
- 首先引入熵:
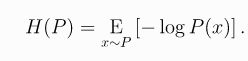
- 得到
Entropy-Regularized Reinforcement Learning, 然后在原本求Return期望max的基础上多引入熵这一项,得到:

- 注意上面用的是无限、折扣reward
- 然后相应的就可以得到:

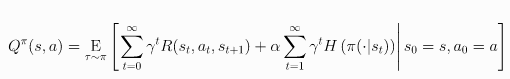
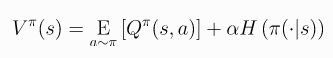


- 其中前者只支持连续动作空间,后者可以支持离散动作空间。
- Q函数的学习方式与 TD3 类似,但有一些关键区别。相似之处包括:
- 就像在 TD3 中一样,两个 Q 函数都是通过回归到单个共享目标的 MSBE 最小化来学习的。
- 与 TD3 一样,使用:
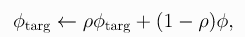
- 与 TD3 一样,共享目标使用了Clipped Double-Q Learning trick。
- 和TD3差异有什么呢?
- 与 TD3 不同,目标还包括一个来自 SAC 使用熵正则化项。
- 与 TD3 不同,目标中使用的下一状态动作来自当前策略而不是目标策略。
- 与 TD3 不同,没有明确的目标策略平滑。TD3 训练确定性策略,因此它通过向下一状态动作添加随机噪声来实现平滑。SAC 训练随机策略,因此随机性的噪声足以获得类似的效果。
- 算法为:

- 对比TD3为:

- 对比DDPG为:

(7) Asynchronous Advantage Actor-Critic (A2C / A3C)
-
异步优势AC算法
-
今天我们会来说说强化学习中的一种有效利用计算资源, 并且能提升训练效用的算法, Asynchronous Advantage Actor-Critic, 简称 A3C.

-
平行宇宙:想像现在有三个平行宇宙, 那么就意味着这3个平行宇宙上存在3个你, 而你可能在电脑前呆了很久, 被催促起来做运动,这3个你都开始活动筋骨啦. 假设3个你都能互相通信, 告诉对方, “我这个动作可以有效缓解我的颈椎病”, “我做那个动作后, 腰就不痛了 “, “我活动了手臂, 肩膀就不痛了”. 这样你是不是就同时学到了对身体好的三招. 这样是不是感觉特别有效率. 让你看看更有效率的, 那就想想3个你同时在写作业, 一共3题, 每人做一题, 只用了1/3 的时间就把作业做完了. 感觉棒棒的. 如果把这种方法用到强化学习, 岂不是效率贼高.

-
平行训练:这就是传说中的 A3C. A3C 其实只是这种平行方式的一种而已, 它采用的是我们之前提到的 Actor-Critic 的形式. 为了训练一对 Actor 和 Critic, 我们将它复制多份红色的, 然后同时放在不同的平行宇宙当中, 让他们各自玩各的. 然后每个红色副本都悄悄告诉黑色的 Actor-Critic 自己在那边的世界玩得怎么样, 有哪些经验值得分享. 然后还能从黑色的 Actor-Critic 这边再次获取综合考量所有副本经验后的通关秘籍. 这样一来一回, 形成了一种有效率的强化学习方式.
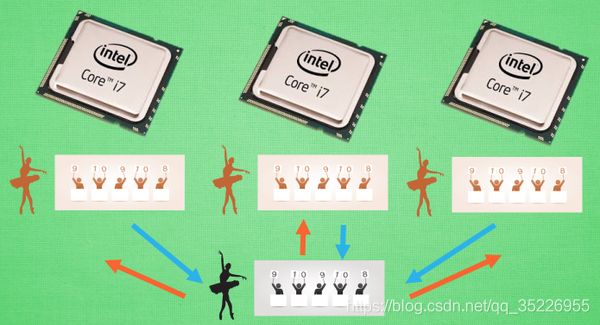
-
多核训练:我们知道目前的计算机多半是有双核, 4核, 甚至 6核, 8核. 一般的学习方法, 我们只能让机器人在一个核上面玩耍. 但是如果使用 A3C 的方法, 我们可以给他们安排去不同的核, 并行运算. 实验结果就是, 这样的计算方式往往比传统的方式快上好多倍. 那我们也多用用这样的红利吧.
-
一句话概括 A3C: Google DeepMind 提出的一种解决 Actor-Critic 不收敛问题的算法. 它会创建多个并行的环境, 让多个拥有副结构的 agent 同时在这些并行环境上更新主结构中的参数. 并行中的 agent 们互不干扰, 而主结构的参数更新受到副结构提交更新的不连续性干扰, 所以更新的相关性被降低, 收敛性提高.
2.3 模仿学习

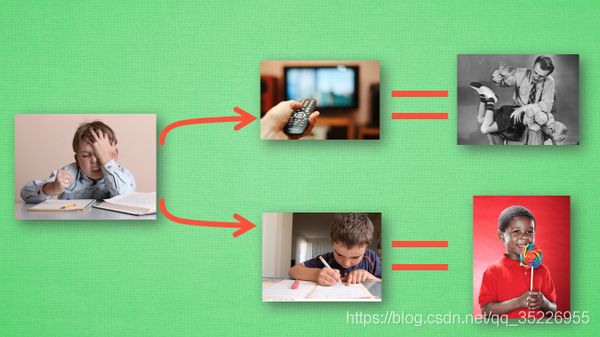
模仿学习指的是从给定的展示中进行学习。机器在这个过程中,也和环境进行交互,但是,并没有显示的得到 reward。在某些任务上,也很难定义 reward。如:自动驾驶,撞死一人,reward为多少,撞到一辆车,reward 为多少,撞到小动物,reward 为多少,撞到 X,reward 又是多少,诸如此类。。。而某些人类所定义的 reward,可能会造成不可控制的行为,如:我们想让 agent 去考试,目标是让其考 100,那么,这个 agent 则可能会为了考 100,而采取作弊的方式,那么,这个就比较尴尬了,是吧 ?我们当然想让 agent 在学习到某些本领的同时,能遵守一定的规则。给他们展示怎么做,然后让其自己去学习,会是一个比较好的方式。
本文所涉及的三种方法:1. 行为克隆,2. 逆强化学习,3. GAN 的方法。
2.3.1 行为克隆(Behavior Cloning)
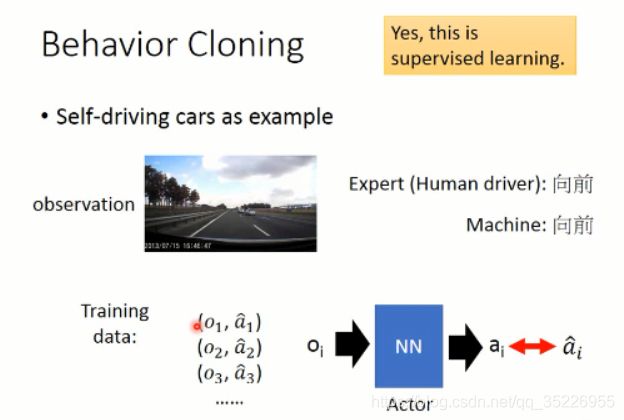
这里以自动驾驶为例,首先我们要收集一堆数据,就是 demo,然后人类做什么,就让机器做什么。其实就是监督学习(supervised learning),让 agent 选择的动作和 给定的动作是一致的。。。
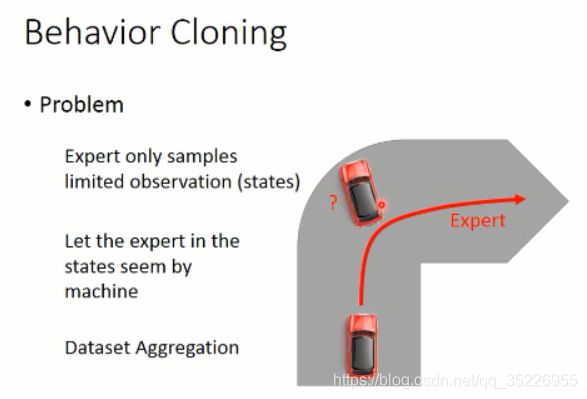
但是,这个方法是有问题的,因为 你给定的 data,是有限的,而且是有限制的。那么,在其他数据上进行测试,则可能不会很好。因此,要么你增加 training data,加入平常 agent 没有看到过的数据,即:dataset aggregation 。
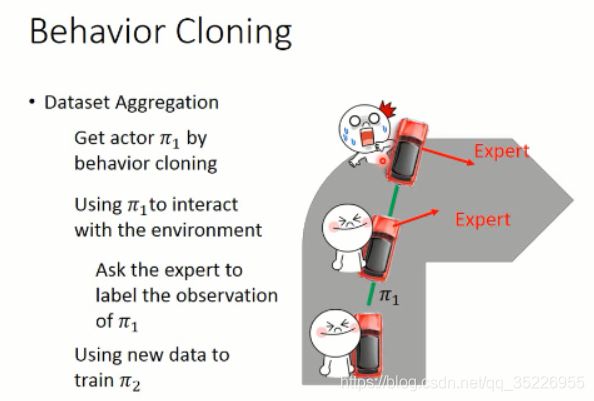
通过不断地增加数据,那么,就可以很好的改进 agent 的策略。有些场景下,也许适应这种方法。。。

而且,你的观测数据 和 策略是有联系的。因为在监督学习当中,我们需要 training data 和 test data 独立同分布。但是,有时候,这两者是不同的(比如跨域ReID等跨域问题,就要做域适应/迁移学习了),那么,就惨了。。。
于是,另一类方法,出现了,即:Inverse Reinforcement Learning (也称为:Inverse Optimal Control,Inverse Optimal Planning)。
2.3.2 逆强化学习(Inverse Reinforcement Learning)
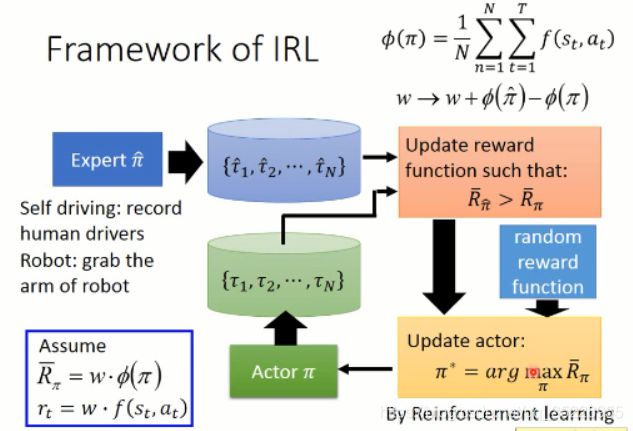
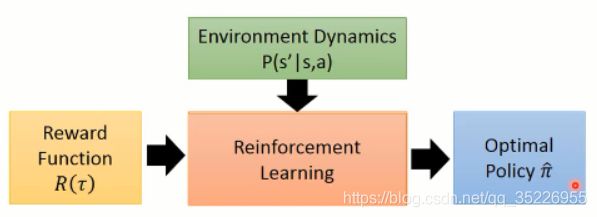
顾名思义,IRL 是 反过来的 RL,RL 是根据 reward 进行参数的调整,然后得到一个 policy。大致流程应该是这个样子:
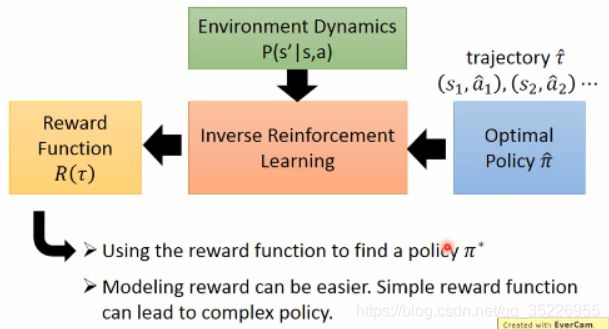
但是, IRL 就不同了,因为他没有显示的 reward,只能根据 人类行为,进行 reward的估计(反推 reward 的函数)。

在得到 reward 函数估计出来之后,再进行 策略函数的估计。。。
原本的 RL,就是给定一个 reward function R(t)(奖励的加和,即回报),然后,这里我们回顾一下 RL 的大致过程(这里以 policy gradient 方法为例)

而 Inverse Reinforcement Learning 这是下面的这个思路:

逆强化学习 则是在给定一个专家之后(expert policy),通过不断地寻找 reward function 来满足给定的 statement(即,解释专家的行为,explaining expert behavior)。。。专家的这个回报是最大的,英雄级别的,比任何其他的 actor 得到的都多。。。
2.3.3 生成对抗模仿学习(GAN for Imitation Learning )

那么如何用 GAN 来做这个事情呢?对应到这件事情上,我们知道,我们想得到的 轨迹 是属于某一个高维的空间中,而 expert 给定的那些轨迹,我们假设是属于一个 distribution,我们想让我们的 model,也去 predict 一个分布出来,然后使得这两者之间尽可能的接近。从而完成 actor 的训练过程,示意图如下所示:

算法流程如下:

Discriminator:尽可能的区分轨迹是由expert生成还是Generator生成。
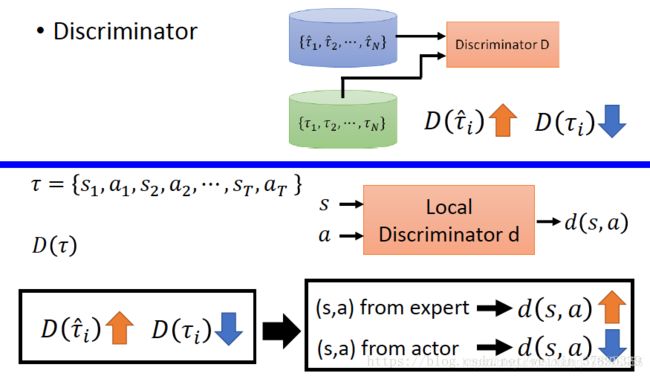
Generator(Actor):产生出一个轨迹,使其与专家轨迹尽可能相近,使Discriminator无法区分轨迹是expert生成的还是Generator生成的。

其算法可以写为:

GAIL能够直接从专家轨迹中学得策略,绕过很多IRL的中间步骤。

参考博客:模仿学习
参考博客:GANIL