强化学习的学习之路(二十)_2021-01-20:Priority Replay Buffer
作为一个新手,写这个强化学习-基础知识专栏是想和大家分享一下自己学习强化学习的学习历程,希望对大家能有所帮助。这个系列后面会不断更新,希望自己在2021年能保证平均每日一更的更新速度,主要是介绍强化学习的基础知识,后面也会更新强化学习的论文阅读专栏。本来是想每一篇多更新一点内容的,后面发现大家上CSDN主要是来提问的,就把很多拆分开来了(而且这样每天任务量也小一点哈哈哈哈偷懒大法)。但是我还是希望知识点能成系统,所以我在目录里面都好按章节系统地写的,而且在github上写成了书籍的形式,如果大家觉得有帮助,希望从头看的话欢迎关注我的github啊,谢谢大家!另外我还会分享深度学习-基础知识专栏以及深度学习-论文阅读专栏,很早以前就和小伙伴们花了很多精力写的,如果有对深度学习感兴趣的小伙伴也欢迎大家关注啊。大家一起互相学习啊!可能会有很多错漏,希望大家批评指正!不要高估一年的努力,也不要低估十年的积累,与君共勉!
接下来的几个博客将会分享以下有关DQN算法及其改进,包括DQN(Nature)、Double DQN、 Multi-step DQN、Pirority Replay Buffer、 Dueling DQN、DQN from Demonstrations、Distributional DQN、Noisy DQN、Q-learning with continuous actions、Rainbow、Practical tips for DQN等。
Priority Replay Buffer
Priority Replay Buffer 是一种针对 Replay Buffer 的改进结构,它来自论文 Prioritized Experience Replay 。在最传统的DQN中,从 Replay Buffer中采集样本时,每一个样本都会以相同的概率被采样出来。也就是说,每一个样本,都会以相同的频率被学习。但实际上,每一个样本的难度是不同的,学习每一个样本得到的收获也不同。有的样本相对简单,表现相对较好,学习得到的收获不会太高; 有的样本则有些困难,表现也相对较差,经过学习后模型会有显著的提高,就像人脑中的记忆也会存在重要性的差别。 如果平等地看待每一个样本,就会在那些简单的样本上花费比较多的时间,而学习的潜力没有被充分挖掘出来。
Priority Replay Buffer 则很好地解决了这个问题。它会根据模型对当前样本的表现情况,给样本一定的权重,在采样时样本被采样的概率就和这个权重有关。交互时表现得越差,对应的权重越高,采样的概率也就越高;反过来,交互时表现得越好,那么权 重也就越低,采样的概率也就越低。
这样,那些使模型表现不好的样本可以有更高的概率被重新学习,模型就会把更多的精力放在这些样本上,模型的学习效率就会有一定的提升。现在,Priority Replay Buffer 已经被广泛应用在 Q-Learning 的算法中,而且这个思想也被神经科学界证实,在人脑上也存在类似的学习机制。
接下来。从算法原理上看,两者的差别在以下两个方面。
(1)为每一个存入 Replay Buffer 的样本设定一个权重。
(2)使用这个权重完成采样过程。
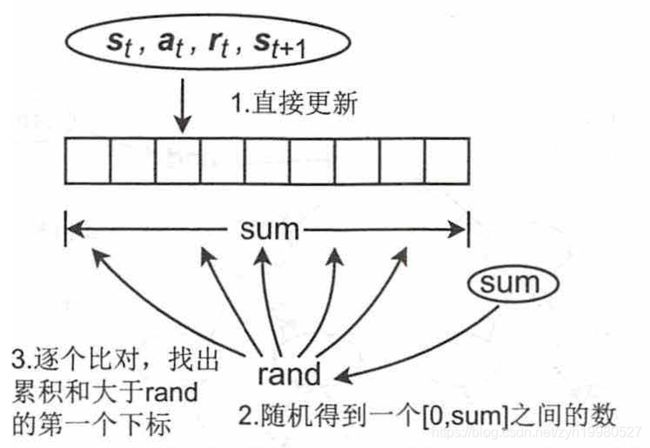
我们先来解决第 2 个问题。假设权重已经得到,我们就可以采用轮盘赌的方法进行样本的采样。如果像 Replay Buffer 一样直接使用数组保存每一个样本和权重,它的更改样本和采样的流程如图下图所示:
流程分为 3 步: 在添加样本到 Replay Buffer 时,直接将其写入而不做任何处理,同时更新 Replay Buffer 中所有样本的权重总和 sum; 在采样时随机得到一个 [0,sum] 之间 的数,那么从 Replay Buffer 算起,累积权重和超过随机值的第一个样本就被选择为待训练的样本,它的运算复杂度如下。
-
更改复杂度: O(1),只需要在指定的位置写人信息。
-
采样复杂度: O(N),需要按序扫描指定的位置才能结束,最坏的情况下可能会扫描整个数组。
从上面的分析可以看出,采样的复杂度有些高,Replay Buffer 的大小一般比较大, 有时可能会接近达到上百万,那么扫描整个数组的代价就会比较大。 为了能快速实现样本集合中一部分样本的权重修改和集合的采样,我们可以采用线段树这个数据结构实现这个功能。线段树能够以比较快的速度更新局部的统计信息,同时可以利用这些信息快速查找满足某些特征的数据。线段树的结构如图下图所示:
线段树的主体是由一棵树构成的。它的叶子节点存放着每一个元素个体的信息,例如它的权重,而线段树的非叶子节点则存放着其子节点的权重汇总。
如果这是一颗求和的线段树,那么非叶子节点存放着其叶子节点的权重总和;
如果这是一颗求最小值的线段树,那么非叶子节点存放着其叶子节点的最小值。使用线段树后的更新与采样的流程如下图所示:
它的流程同样有 3 步。
在添加样本到 Replay Buffer 时,不光记录样本信息,还要沿着样本叶子出发,依次找到叶子节点的父节点,更新父节点的权值;
在采样时同样得到一个随机数,然后利用树的结构二分查找就可以快速定位被选到的样本,它的运算复杂度如下:
- 更改复杂度: O(log N),需要更新叶子节点的所有父节点的信息。
- 采样复杂度: O ( log N ) , O(\log N), O(logN), 只需要从根出发访问指定的叶子。
对比发现,线段树在采样上明显快于数组,而更新的代价又没有增加太多,因此它可以替代数组使用。
我们又知道,Priority Replay Buffer 的主要思路是增加有价值样本出现的频率。那么我们该如何定义“有价值”这个概念呢?
最直观的想法是,能让模型学习到更多的内容,这个样本一定更有价值。那么,什么样的样本能让模型学习到更多呢? 当然是能产生更大的 TD-Error 的,即估计值与目标值的差距越大,样本越有价值。所以我们可以将 TD-Error 作为样本重要性的衡量指标。TD-Error 越高,样本出现的概率就越高。
虽然 TD-Error 是一个很合理的指标,但是由于我们的模型处在学习的过程中,在样本放入 Priority Replay Buffer 时样本的 TD-Error 和它被取出时的 TD-Error 有可能不一样。
所以可能会出现一种情况:一个样本在放入时 TD-Error 很高,但是随着模型的不断学习,模型对这个样本的实际 TD-Error 已经降低,但它还是会以很高的概率出现。
一个最合理的方法,是在我们从 Priority Replay Buffer 取出样本时,将它的 TD-Error 重新计算一遍,但是这样做的代价实在太大**,所以我们只好使用样本放人 Priority Replay Buffer 时的 TD-Error 作为近似。**
既然我们已经知道这个指标并不完全可靠,就需要其他的方法辅助。因此我们要 确保 TD-Error 较高的样本出现的概率更高,同时也要使那些 TD-Error 较低的样本以一定的概率出现。论文中定义的一个计算样本出现概率的方法为
P ( i ) = p i α ∑ k p k α P(i)=\frac{p_{i}^{\alpha}}{\sum_{k} p_{k}^{\alpha}} P(i)=∑kpkαpiα
其中 p i p_{i} pi 表示每个样本在计算时的 TD-Error。 可以调整样本 TD-Error 的重要性。
当 α = 1 \alpha=1 α=1 时,相当于我们直接使用 TD-Error 数值 ;
当 α < 1 \alpha<1 α<1 时,我们就可以削弱高 TD-Error 样本的影响,增强低 TD-Error 样本的影响。(感觉这里就和softmax刚好相反)。
这样我们就可以通过这个参数调整Priority Replay Buffer 的表现。
除了上面提到的两个不同,实际上 Priority Replay Buffer 还做了第三个改变,它提 供了一个参数,用于调整每个样本对模型更新的影响。
对 Replay Buffer 来说,每一个样本是被等概率取出的,它们对模型的更新也是等权重的; 而 Priority Replay Buffer 的 样本是非等概率取出的,它的样本服从另一个难以清楚地描述的分布,所以我们对模型的更新是有偏差的。
为了使我们的更新无偏,可以采用重要性采样的方法使更新变得无偏,对应的公式为
E i ∼ R B [ ∇ J ] = E i ∼ P R B [ P R B ( i ) P P R B ( i ) ∇ J ] = E i ∼ P R B [ 1 N P P R B ( i ) ∇ J ] = E i ∼ P R B [ 1 N ⋅ P P R B ( i ) ∇ J ] \begin{aligned} E_{i \sim \mathrm{RB}}[\nabla J] &=E_{i \sim \mathrm{PRB}}\left[\frac{P_{\mathrm{RB}}(i)}{P_{\mathrm{PRB}}(i)} \nabla J\right] \\ &=E_{i \sim \mathrm{PRB}}\left[\frac{\frac{1}{N}}{P_{\mathrm{PRB}}(i)} \nabla J\right] \\ &=E_{i \sim \mathrm{PRB}}\left[\frac{1}{N \cdot P_{\mathrm{PRB}}(i)} \nabla J\right] \end{aligned} Ei∼RB[∇J]=Ei∼PRB[PPRB(i)PRB(i)∇J]=Ei∼PRB[PPRB(i)N1∇J]=Ei∼PRB[N⋅PPRB(i)1∇J]
其中 N 表示 Replay Buffer 存放的样本数量。所以我们可以在每一个被学习的样本前增 加一个权重 1 N ⋅ P PRB ( i ) , \frac{1}{N \cdot P_{\text {PRB }(i)}}, N⋅PPRB (i)1, 这样就可以使更新变得无偏。
我们使用 Priority Replay Buffer 的目的不正是让更新变得有偏吗?为什么还要削弱它的优势呢?实际上,这个纠正是为了说明我们可以通过一些设定让它变回 Replay Buffer 那样的更新方式,这样虽然没有带来任何好处,但也没有任何坏处。
那么我们就可以根据实际问题调整这个权重,让它在两种更新效果之间做一个权衡,既能确保提升样本的利用率,又能确保结果不会带来太大的偏差,新的权重更新公式变为
w i = ( 1 N ⋅ P P R B ( i ) ) β w_{i}=\left(\frac{1}{N \cdot P_{\mathrm{PRB}}(i)}\right)^{\beta} wi=(N⋅PPRB(i)1)β
这样当 β = 1 \beta=1 β=1 时,更新效果实际上等同于 Replay Buffer; 当 β < 1 \beta<1 β<1 时,Priority Replay Buffer 就能够发挥作用了。
以上是 Priority Replay Buffer 的算法原理,在此我们可以做一个总结。
(1)在样本存入 Replay Buffer 时,计算 P ( i ) = ∑ j p ( i ) α P(i)=\sum_{j} p(i)^{\alpha} P(i)=∑jp(i)α
(2)在样本取出时,以第 1 步计算得到的概率进行采样。
(3)在更新时,为每一个样本添加 w i = ( 1 N ⋅ P PBB ( i ) ) β w_{i}=\left(\frac{1}{N \cdot P_{\text {PBB }(i)}}\right)^{\beta} wi=(N⋅PPBB (i)1)β 的权重。
(4)随着训练的进行,让 β \beta β 从某个小于 1 的值渐进地靠近 1。
上一篇:强化学习的学习之路(十九)_2021-01-19: Multi-step DQN
下一篇:强化学习的学习之路(二十一)_2021-01-21: Dueling DQN(Dueling networkarchitectures for deep reinforcement learning)