Umap高维数据可视化与降维
Umap解决高维数据可视化的问题,以及高效降维。
Umap地址:https://github.com/lmcinnes/umap
文档地址:UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction — umap 0.5 documentation
1.pip通过清华镜像安装方式:
pip install umap-learn[plot] -i https://pypi.tuna.tsinghua.edu.cn/simple2.使用方式
2.1连续性数据的可视化
# Umap的纯连续型数据降维与可视化
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_diabetes
from sklearn.svm import SVR
import umap
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
%matplotlib inline# 加载是数据集
load = load_diabetes()
data = pd.DataFrame(load.data)
data.columns = load.feature_names
target = load.target# 对特征数据进行标准化
scaled_data = StandardScaler().fit_transform(data)
# 使用umap对数据进行降维
embedding = umap.UMAP().fit_transform(scaled_data)
embedding.shape ![]()
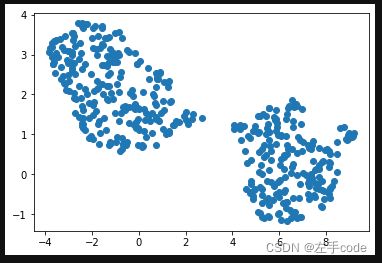
# 对降维后的数据画图
plt.scatter(embedding[:, 0],embedding[:, 1])2.2对分类数据降维(含标签)
使用sklearn的手写数字来做数据可视化
# 分类手写数据的可视化
from sklearn.datasets import load_digits
digits = load_digits()reducer = umap.UMAP(random_state=42)
reducer.fit(digits.data)
embedding = reducer.transform(digits.data)
# Verify that the result of calling transform is
# idenitical to accessing the embedding_ attribute
assert(np.all(embedding == reducer.embedding_))
embedding.shape画图
plt.figure(figsize=(15,10))
plt.scatter(embedding[:, 0], embedding[:, 1], c=digits.target, cmap='Spectral', s=5)
plt.gca().set_aspect('equal', 'datalim')
plt.colorbar(boundaries=np.arange(11)-0.5).set_ticks(np.arange(10))
plt.title('UMAP projection of the Digits dataset', fontsize=24);2.3对混合数据(离散、连续)在分别降维后组合在一起进行可视化
使用seaborn的钻石数据集
#####对混合数据(离散、连续)在分别降维后组合在一起进行可视化
# 砖石数据
from sklearn.preprocessing import RobustScaler
import umap.plot
diamonds = sns.load_dataset('diamonds')
diamonds.head()price是标签,其余是特征
# 离散数据与连续数据的划分
numeric = diamonds[["carat", "table", "x", "y", "z"]].copy()
ordinal = diamonds[["cut", "color", "clarity"]].copy()
# 连续数据预处理
scaled_numeric = RobustScaler().fit_transform(numeric)
scaled_numeric[:5]
# 离散数据数据因与顺序有关所以以数字划分表示等级
# 若离散数据与顺序无关,则使用独热编码后,UMAP设置参数metric为dice
ordinal["cut"] = ordinal.cut.map({"Fair":0, "Good":1, "Very Good":2, "Premium":3, "Ideal":4})
ordinal["color"] = ordinal.color.map({"D":0, "E":1, "F":2, "G":3, "H":4, "I":5, "J":6})
ordinal["clarity"] = ordinal.clarity.map({"I1":0, "SI2":1, "SI1":2, "VS2":3, "VS1":4, "VVS2":5, "VVS1":6, "IF":7})
# 分别对数据进行降维,因分类数据与顺序有关所以设置参数为metric="manhattan"
numeric_mapper = umap.UMAP(n_neighbors=15, random_state=42).fit(scaled_numeric)
ordinal_mapper = umap.UMAP(metric="manhattan", n_neighbors=150, random_state=42).fit(ordinal.values)
# 对连续数据进行画图,
umap.plot.points(numeric_mapper, values=diamonds["price"], cmap="viridis")# 对分类数据分别画图
fig, ax = umap.plot.plt.subplots(2, 2, figsize=(12,12))
umap.plot.points(ordinal_mapper, labels=diamonds["color"], ax=ax[0,0])
umap.plot.points(ordinal_mapper, labels=diamonds["clarity"], ax=ax[0,1])
umap.plot.points(ordinal_mapper, labels=diamonds["cut"], ax=ax[1,0])
umap.plot.points(ordinal_mapper, values=diamonds["price"], cmap="viridis", ax=ax[1,1])"""
这里有三种组合方式
那么,假设我们不能只是将原始数据粘合在一起并在其上贴上合理的指标,我们能做什么?
我们可以对模糊拓扑表示进行交集或并集。 还需要做一些工作来重申 UMAP 的理论假设(局部连通性,近似均匀分布)。
幸运的是,只要您手头有适合的 UMAP 模型的副本(我们在这种情况下就是这样做的),UMAP 就可以使这相对容易。
要使两个模型相交,只需使用 * 运算符; 使用 + 运算符来联合它们。
"""
intersection_mapper = numeric_mapper * ordinal_mapper
union_mapper = numeric_mapper + ordinal_mapper
contrast_mapper = numeric_mapper - ordinal_mapper# 并集
umap.plot.points(union_mapper, labels=diamonds["color"])# 差集
umap.plot.points(contrast_mapper, values=diamonds["price"], cmap="viridis")3.类的说明
class UMAP(BaseEstimator):
"""Uniform Manifold Approximation and Projection
Finds a low dimensional embedding of the data that approximates
an underlying manifold.
Parameters
----------
n_neighbors: float (optional, default 15)
The size of local neighborhood (in terms of number of neighboring
sample points) used for manifold approximation. Larger values
result in more global views of the manifold, while smaller
values result in more local data being preserved. In general
values should be in the range 2 to 100.
n_components: int (optional, default 2)
The dimension of the space to embed into. This defaults to 2 to
provide easy visualization, but can reasonably be set to any
integer value in the range 2 to 100.
metric: string or function (optional, default 'euclidean')
The metric to use to compute distances in high dimensional space.
If a string is passed it must match a valid predefined metric. If
a general metric is required a function that takes two 1d arrays and
returns a float can be provided. For performance purposes it is
required that this be a numba jit'd function. Valid string metrics
include:
* euclidean
* manhattan
* chebyshev
* minkowski
* canberra
* braycurtis
* mahalanobis
* wminkowski
* seuclidean
* cosine
* correlation
* haversine
* hamming
* jaccard
* dice
* russelrao
* kulsinski
* ll_dirichlet
* hellinger
* rogerstanimoto
* sokalmichener
* sokalsneath
* yule
Metrics that take arguments (such as minkowski, mahalanobis etc.)
can have arguments passed via the metric_kwds dictionary. At this
time care must be taken and dictionary elements must be ordered
appropriately; this will hopefully be fixed in the future.
n_epochs: int (optional, default None)
The number of training epochs to be used in optimizing the
low dimensional embedding. Larger values result in more accurate
embeddings. If None is specified a value will be selected based on
the size of the input dataset (200 for large datasets, 500 for small).
learning_rate: float (optional, default 1.0)
The initial learning rate for the embedding optimization.
init: string (optional, default 'spectral')
How to initialize the low dimensional embedding. Options are:
* 'spectral': use a spectral embedding of the fuzzy 1-skeleton
* 'random': assign initial embedding positions at random.
* A numpy array of initial embedding positions.
min_dist: float (optional, default 0.1)
The effective minimum distance between embedded points. Smaller values
will result in a more clustered/clumped embedding where nearby points
on the manifold are drawn closer together, while larger values will
result on a more even dispersal of points. The value should be set
relative to the ``spread`` value, which determines the scale at which
embedded points will be spread out.
spread: float (optional, default 1.0)
The effective scale of embedded points. In combination with ``min_dist``
this determines how clustered/clumped the embedded points are.
low_memory: bool (optional, default True)
For some datasets the nearest neighbor computation can consume a lot of
memory. If you find that UMAP is failing due to memory constraints
consider setting this option to True. This approach is more
computationally expensive, but avoids excessive memory use.
set_op_mix_ratio: float (optional, default 1.0)
Interpolate between (fuzzy) union and intersection as the set operation
used to combine local fuzzy simplicial sets to obtain a global fuzzy
simplicial sets. Both fuzzy set operations use the product t-norm.
The value of this parameter should be between 0.0 and 1.0; a value of
1.0 will use a pure fuzzy union, while 0.0 will use a pure fuzzy
intersection.
local_connectivity: int (optional, default 1)
The local connectivity required -- i.e. the number of nearest
neighbors that should be assumed to be connected at a local level.
The higher this value the more connected the manifold becomes
locally. In practice this should be not more than the local intrinsic
dimension of the manifold.
repulsion_strength: float (optional, default 1.0)
Weighting applied to negative samples in low dimensional embedding
optimization. Values higher than one will result in greater weight
being given to negative samples.
negative_sample_rate: int (optional, default 5)
The number of negative samples to select per positive sample
in the optimization process. Increasing this value will result
in greater repulsive force being applied, greater optimization
cost, but slightly more accuracy.
transform_queue_size: float (optional, default 4.0)
For transform operations (embedding new points using a trained model_
this will control how aggressively to search for nearest neighbors.
Larger values will result in slower performance but more accurate
nearest neighbor evaluation.
a: float (optional, default None)
More specific parameters controlling the embedding. If None these
values are set automatically as determined by ``min_dist`` and
``spread``.
b: float (optional, default None)
More specific parameters controlling the embedding. If None these
values are set automatically as determined by ``min_dist`` and
``spread``.
random_state: int, RandomState instance or None, optional (default: None)
If int, random_state is the seed used by the random number generator;
If RandomState instance, random_state is the random number generator;
If None, the random number generator is the RandomState instance used
by `np.random`.
metric_kwds: dict (optional, default None)
Arguments to pass on to the metric, such as the ``p`` value for
Minkowski distance. If None then no arguments are passed on.
angular_rp_forest: bool (optional, default False)
Whether to use an angular random projection forest to initialise
the approximate nearest neighbor search. This can be faster, but is
mostly on useful for metric that use an angular style distance such
as cosine, correlation etc. In the case of those metrics angular forests
will be chosen automatically.
target_n_neighbors: int (optional, default -1)
The number of nearest neighbors to use to construct the target simplcial
set. If set to -1 use the ``n_neighbors`` value.
target_metric: string or callable (optional, default 'categorical')
The metric used to measure distance for a target array is using supervised
dimension reduction. By default this is 'categorical' which will measure
distance in terms of whether categories match or are different. Furthermore,
if semi-supervised is required target values of -1 will be trated as
unlabelled under the 'categorical' metric. If the target array takes
continuous values (e.g. for a regression problem) then metric of 'l1'
or 'l2' is probably more appropriate.
target_metric_kwds: dict (optional, default None)
Keyword argument to pass to the target metric when performing
supervised dimension reduction. If None then no arguments are passed on.
target_weight: float (optional, default 0.5)
weighting factor between data topology and target topology. A value of
0.0 weights predominantly on data, a value of 1.0 places a strong emphasis on
target. The default of 0.5 balances the weighting equally between data and
target.
transform_seed: int (optional, default 42)
Random seed used for the stochastic aspects of the transform operation.
This ensures consistency in transform operations.
verbose: bool (optional, default False)
Controls verbosity of logging.
tqdm_kwds: dict (optional, defaul None)
Key word arguments to be used by the tqdm progress bar.
unique: bool (optional, default False)
Controls if the rows of your data should be uniqued before being
embedded. If you have more duplicates than you have n_neighbour
you can have the identical data points lying in different regions of
your space. It also violates the definition of a metric.
For to map from internal structures back to your data use the variable
_unique_inverse_.
densmap: bool (optional, default False)
Specifies whether the density-augmented objective of densMAP
should be used for optimization. Turning on this option generates
an embedding where the local densities are encouraged to be correlated
with those in the original space. Parameters below with the prefix 'dens'
further control the behavior of this extension.
dens_lambda: float (optional, default 2.0)
Controls the regularization weight of the density correlation term
in densMAP. Higher values prioritize density preservation over the
UMAP objective, and vice versa for values closer to zero. Setting this
parameter to zero is equivalent to running the original UMAP algorithm.
dens_frac: float (optional, default 0.3)
Controls the fraction of epochs (between 0 and 1) where the
density-augmented objective is used in densMAP. The first
(1 - dens_frac) fraction of epochs optimize the original UMAP objective
before introducing the density correlation term.
dens_var_shift: float (optional, default 0.1)
A small constant added to the variance of local radii in the
embedding when calculating the density correlation objective to
prevent numerical instability from dividing by a small number
output_dens: float (optional, default False)
Determines whether the local radii of the final embedding (an inverse
measure of local density) are computed and returned in addition to
the embedding. If set to True, local radii of the original data
are also included in the output for comparison; the output is a tuple
(embedding, original local radii, embedding local radii). This option
can also be used when densmap=False to calculate the densities for
UMAP embeddings.
disconnection_distance: float (optional, default np.inf or maximal value for bounded distances)
Disconnect any vertices of distance greater than or equal to disconnection_distance when approximating the
manifold via our k-nn graph. This is particularly useful in the case that you have a bounded metric. The
UMAP assumption that we have a connected manifold can be problematic when you have points that are maximally
different from all the rest of your data. The connected manifold assumption will make such points have perfect
similarity to a random set of other points. Too many such points will artificially connect your space.
precomputed_knn: tuple (optional, default (None,None,None))
If the k-nearest neighbors of each point has already been calculated you
can pass them in here to save computation time. The number of nearest
neighbors in the precomputed_knn must be greater or equal to the
n_neighbors parameter. This should be a tuple containing the output
of the nearest_neighbors() function or attributes from a previously fit
UMAP object; (knn_indices, knn_dists,knn_search_index).
"""
def points(
umap_object,
labels=None,
values=None,
theme=None,
cmap="Blues",
color_key=None,
color_key_cmap="Spectral",
background="white",
width=800,
height=800,
show_legend=True,
subset_points=None,
ax=None,
alpha=None,
):
"""Plot an embedding as points. Currently this only works
for 2D embeddings. While there are many optional parameters
to further control and tailor the plotting, you need only
pass in the trained/fit umap model to get results. This plot
utility will attempt to do the hard work of avoiding
overplotting issues, and make it easy to automatically
colour points by a categorical labelling or numeric values.
This method is intended to be used within a Jupyter
notebook with ``%matplotlib inline``.
Parameters
----------
umap_object: trained UMAP object
A trained UMAP object that has a 2D embedding.
labels: array, shape (n_samples,) (optional, default None)
An array of labels (assumed integer or categorical),
one for each data sample.
This will be used for coloring the points in
the plot according to their label. Note that
this option is mutually exclusive to the ``values``
option.
values: array, shape (n_samples,) (optional, default None)
An array of values (assumed float or continuous),
one for each sample.
This will be used for coloring the points in
the plot according to a colorscale associated
to the total range of values. Note that this
option is mutually exclusive to the ``labels``
option.
theme: string (optional, default None)
A color theme to use for plotting. A small set of
predefined themes are provided which have relatively
good aesthetics. Available themes are:
* 'blue'
* 'red'
* 'green'
* 'inferno'
* 'fire'
* 'viridis'
* 'darkblue'
* 'darkred'
* 'darkgreen'
cmap: string (optional, default 'Blues')
The name of a matplotlib colormap to use for coloring
or shading points. If no labels or values are passed
this will be used for shading points according to
density (largely only of relevance for very large
datasets). If values are passed this will be used for
shading according the value. Note that if theme
is passed then this value will be overridden by the
corresponding option of the theme.
color_key: dict or array, shape (n_categories) (optional, default None)
A way to assign colors to categoricals. This can either be
an explicit dict mapping labels to colors (as strings of form
'#RRGGBB'), or an array like object providing one color for
each distinct category being provided in ``labels``. Either
way this mapping will be used to color points according to
the label. Note that if theme
is passed then this value will be overridden by the
corresponding option of the theme.
color_key_cmap: string (optional, default 'Spectral')
The name of a matplotlib colormap to use for categorical coloring.
If an explicit ``color_key`` is not given a color mapping for
categories can be generated from the label list and selecting
a matching list of colors from the given colormap. Note
that if theme
is passed then this value will be overridden by the
corresponding option of the theme.
background: string (optional, default 'white)
The color of the background. Usually this will be either
'white' or 'black', but any color name will work. Ideally
one wants to match this appropriately to the colors being
used for points etc. This is one of the things that themes
handle for you. Note that if theme
is passed then this value will be overridden by the
corresponding option of the theme.
width: int (optional, default 800)
The desired width of the plot in pixels.
height: int (optional, default 800)
The desired height of the plot in pixels
show_legend: bool (optional, default True)
Whether to display a legend of the labels
subset_points: array, shape (n_samples,) (optional, default None)
A way to select a subset of points based on an array of boolean
values.
ax: matplotlib axis (optional, default None)
The matplotlib axis to draw the plot to, or if None, which is
the default, a new axis will be created and returned.
alpha: float (optional, default: None)
The alpha blending value, between 0 (transparent) and 1 (opaque).
Returns
-------
result: matplotlib axis
The result is a matplotlib axis with the relevant plot displayed.
If you are using a notebooks and have ``%matplotlib inline`` set
then this will simply display inline.
"""