数据结构与算法简介

0. 内容说明

最近在自己编写一些小的算法的时候，深感自己的算法过于臃肿。碰巧Datawhale在新的一期组队学习中组织了数据结构与算法的课程学习。于是就参加了，再次感谢Datawhale~~

首先跟大家分享一下两个自己感觉比较好的学习资料，一个是 算法通关手册 ，也是Datawhale在本次组队学习中的学习资料；一个是B站上的视频 【北京大学】数据结构与算法Python版（完整版），老师讲的特别棒（也难得有Python版的数据结构课程，哈哈~）。

需要指出的是：本次博客的内容更像是对上述两个资料做的笔记，很多都是资料上的原内容，并非原创。

1. 数据结构与算法简介

数据结构与算法，顾名思义，就是数据结构与算法（哈哈~）
其中，数据结构研究的是数据的逻辑结构、物理结构以及它们之间的相互关系，并对这种结构定义相应的运算，设计出相应的算法，并确保经过这些运算以后所得到的新结构仍保持原来的结构类型。数据结构主要包含两种：逻辑结构 （数据元素之间的相互关系）和 物理结构（数据的逻辑结构在计算机中的存储方式）。简而言之，逻辑结构刻画了数据之间到底是什么样的关系，而物理结构则刻画了相应的逻辑结构在计算机中到底是怎么保存的。

2 数据结构

2.1 逻辑结构

逻辑结构主要有以下四种（图片来自资料一 算法通关手册 ）

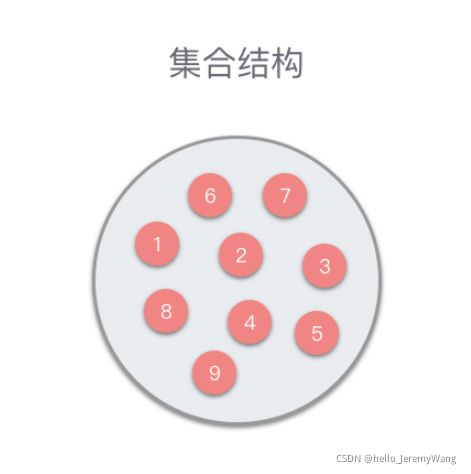
• 集合结构
  集合结构中数据元素同属于一个集合，除此之外无其他关系。从下图可以看出，集合结构只是将数据无序地保存到一个集合内部。需要注意的是，每个数据元素都是唯一的。
  
• 线性结构
  线性结构相对而言比较好理解，直观而言就是将数据保存到一条连续的直线里面了。在线性结构中，数据元素之间是「一对一」关系。
  
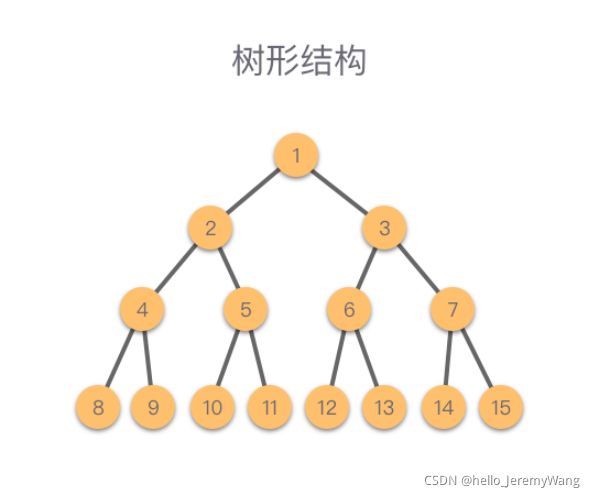
• 树状结构
  树状结构是一种很重要的数据结构，它刻画了数据一对多的层次关系。之前如果学习过决策树的同学应该对树状结构十分清楚。我觉得树状结构最大的特点就是保存了数据之间的层次关系。
  
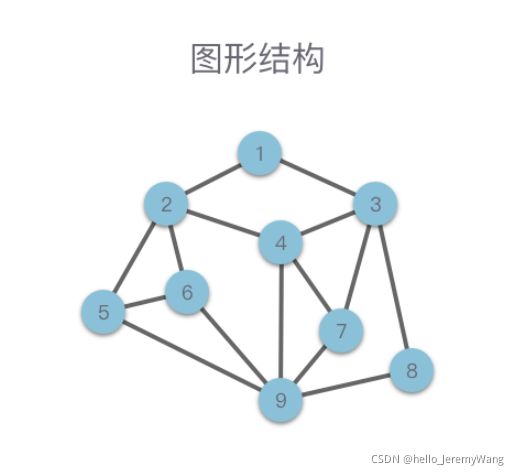
• 图形结构
  图形结构是一种比树形结构更复杂的非线性结构，用于表示物件与物件之间的关系。一张图由一些小圆点（称为顶点或结点）和连结这些圆点的直线或曲线（称为边）组成。如果同学们之前学习过HMM模型、CRF模型等概率图模型的话，应该对图形结构比较熟悉了，它主要刻画了一种数据间的多对多关系。
  

2.2 物理结构

物理结构主要有一下两种（图片来自资料一 算法通关手册 ）

• 顺序存储结构
  顺序存储结构（Sequential Storage Structure）：将数据元素存放在一片地址连续的存储单元里，数据元素之间的逻辑关系通过数据元素的存储地址来直接反映。这种存储结构比较好理解，说白了就是存到一段连续的内存空间里面了，如下图所示：
  

• 链式存储结构
  链式存储结构（Linked Storage Structure）：将数据元素存放在任意的存储单元里，存储单元可以连续，也可以不连续。链式存储结构中，逻辑上相邻的数据元素在物理地址上可能相邻，可也能不相邻。其在物理地址上的表现是随机的。链式存储结构中，一般将每个数据元素占用的若干单元的组合称为一个链结点。每个链结点不仅要存放一个数据元素的数据信息，还要存放一个指出这个数据元素在逻辑关系的直接后继元素所在链结点的地址，该地址被称为指针。数据元素之间的逻辑关系是通过指针来间接反映的。（ 算法通关手册 ）
  说白了，链式存储结构中有两大块：存储的数据，以及存储的地址。不同的数据之间通过存储的地址相互链接，并不需要一定在物理上互相紧邻。
  

3 算法

算法（Algorithm）：解决特定问题求解步骤的准确而完整的描述，在计算机中表现为一系列指令的集合，算法代表着用系统的方法描述解决问题的策略机制。算法所追求的就是 所需运行时间更少（时间复杂度更低）、占用内存空间更小（空间复杂度更低）。

3.1 算法复杂度

在算法中，我们除了要考虑这个算法能不能算出来我们希望得到的结果，还要考虑这个算法的算法复杂度。
算法复杂度主要包含了 时间复杂度 和 空间复杂度 。 时间复杂度说白了就是要多久能算出来，空间复杂度就是需要多大的内存才能算出来。

3.1.1 时间复杂度

时间复杂度主要通过渐进上界符号 O 来刻画。说白了就是刻画了我们需要的复杂度的上界是多少。具体的介绍可以参考 算法通关手册 。

• $O(1)$
  $O(1)$只是常数阶时间复杂度的一种表示方式，并不是指只执行了一行代码。只要代码的执行时间不随着问题规模 n 的增大而增长，这样的算法时间复杂度都记为$O(1)$

def power_2(n):
	a = 2
	result = 2**n
	return result

• $O(n)$
  $O(n)$一般含有非嵌套循环，且单层循环下的语句执行次数为 n 的算法涉及线性时间复杂度。这类算法随着问题规模 n 的增大，对应计算次数呈线性增长。

def sum(n):
	result = 0
	for i in range(n):
		result += 1
	return result

• $O(n^2)$
  $O(n^2)$ 一般含有双层嵌套，且每层循环下的语句执行次数为 n 的算法涉及平方时间复杂度。这类算法随着问题规模 n 的增大，对应计算次数呈平方关系增长。

def sum(n)
	result = 0
	for i in range(n):
		for j in range(n):
			result += 1
	return result

• $O(n!)$
  $O(n!)$阶乘时间复杂度一般出现在与「全排列」相关的算法中。这类算法随着问题规模 n 的增大，对应计算次数呈阶乘关系增长。

def algorithm(n):
	if n <= 0:
		return 1
	return n * algorithm(n - 1)

• $O(logn)$

def algorithm(n):
	cnt = 1
	while cnt < n:
		cnt *= 2
	return cnt

上述代码中 cnt = 1 的时间复杂度为 O(1) 可以忽略不算。while 循环体中 cnt 从 1 开始，每循环一次都乘以 2。当大于 n 时循环结束。变量 cnt 的取值是一个等比数列：$2^0$，$2^1$，$2^2$，…，$2^x$，根据$2^x=n$ ，可以得出这段循环体的执行次数为 $logn$ 。所以这段代码的时间复杂度为 $O(logn)$。

• $O(nlogn)$
  $O(nlogn)$就是在上述$O(logn)$ 的循环中再嵌套一个与之前运算无关的for循环。

def algorithm(n):
	cnt = 1
	res = 0
	while cnt < n:
		cnt *= 2
		for i in range(n):
			res += 1
	return res

算法通关手册 指出，通常情况下，我们的程序的时间复杂度并不是固定了，比如书中列出的这个程序，因为程序可能在第一步就找到需要的数字并使用break语句结束运算，也可能将for循环循环完了才找到需要的数字。那这种情况我们该怎么刻画时间复杂度呢？

def find(nums, val):
	pos = -1
	for i in range(n):
		if nums[i] == val:
			pos = i
			break
	return pos

书中指出：我们应该使用如下的概念来解决这个问题：（一般使用平均时间复杂度来刻画我们的程序）

最佳时间复杂度：每个输入规模下用时最短的输入对应的时间复杂度。
最坏时间复杂度：每个输入规模下用时最长的输入对应的时间复杂度。
平均时间复杂度：每个输入规模下所有可能输入对应用时平均值的复杂度（随机输入下期望用时的复杂度）。
就刚刚那个例子，书中给出了平均复杂度的计算方法：在数组 nums 中查找变量值为 val 的位置，总共有 n + 1 种情况：在数组的 0 ~ n - 1 和 不在数组中。我们将所有情况下，需要执行的语句累加起来，再除以 n + 1，就可以得到平均需要执行的语句，即：$\frac{1+2+3+...+n+n}{n+1}=\frac{n(n+3)}{2(n+1)}$。将公式简化后，得到的平均时间复杂度就是 $O(n)$ 。

3.1.2 空间复杂度

空间复杂度（Space Complexity）：在问题的输入规模为 n 的条件下，算法所占用的空间大小，可以记作为 S(n)。一般将 算法的辅助空间 作为衡量空间复杂度的标准。

• $O(1)$

def algorithm(n):
	a = 1
	b = 2
	res = a * b + n
	return res

上述代码中使用 a、b、res 3 个局部变量，其所占空间大小并不会随着问题规模 n 的在增大而增大，所以该算法的空间复杂度为$O(1)$.

• $O(n)$

def algorithm(n):
	if n <= 0:
		return 1
	return n * algorithm(n - 1)

上述代码采用了递归调用的方式。每次递归调用都占用了 1 个栈帧空间，总共调用了 n 次，所以该算法的空间复杂度为 $O(n)$.