“深度学习”学习日记。卷积神经网络--卷积层与池化层的实现

2023.2.7

一、池化层：

池化是缩小高、长方向上的空间运算。

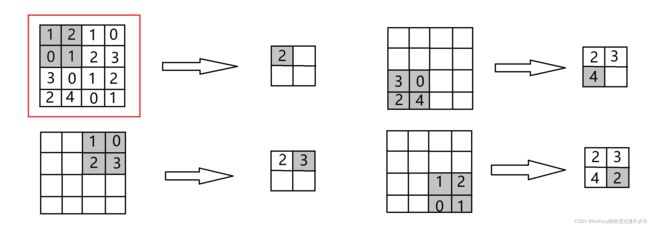
如图，，Max池化的处理步骤，2×2的区域集约成1个元素，缩小空间大小；

除了图中的Max池化之外，还有Average池化等。相对于Max池化是从目标区域中取出最大值，Average池化是计算目标区域的平均值。在图像识别领域，一般使用Max池化。 

 可以很明显的看到，池化的窗口步幅为2，所以2×2的窗口移动间隔2个元素。另外，一般来说池化的窗口大小会和步幅设定成相同的值。

二，池化层的特征：

1，没有学习的参数；

池化层和卷积层不同，没有要学习的参数。池化只是从目标区域中取出最大值或者平均值，所以不存在要学习的参数

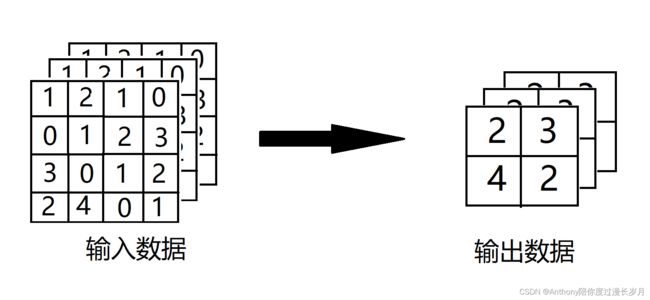
2，通道数不会改变；

经过池化运算，输入数据和输出数据的通道数不会发生改变，池化计算是按通道进行的

如图例：通道数依然是3

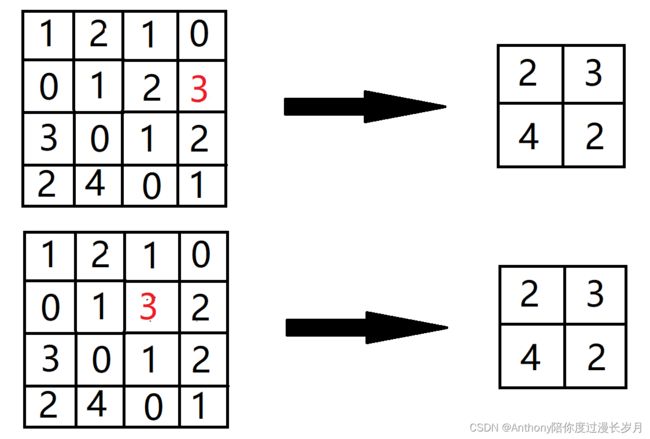
 对微小数字的位置变化具有鲁棒性（抗干扰性）：

输入数据发生微小偏差时，池化人会返回相同的结果

如图例：池化会吸收输入数据的偏差

 三、卷积层与池化层的实现：

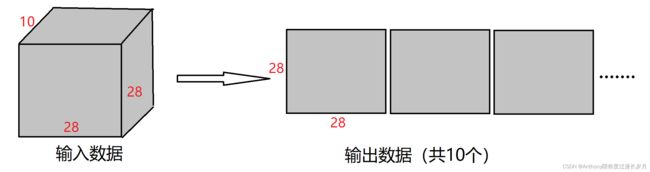
1，4维数组：

在学习卷积层的时候，CNN中各层传递的数据都是4维数据；

参考文章：“深度学习”学习日记。卷积神经网络--卷积层https://blog.csdn.net/m0_72675651/article/details/128861606

用Pyhton实现：

注意一下他们的区别，可以利用索引方便访问想要数据

import numpy as np

x = np.random.rand(10, 1, 28, 28)
print(x)

print(x[0])
print(x[0].shape)  # (1, 28, 28)
print(x[1].shape)  # (1, 28, 28)

print(x[0, 0, 0, 0])  # 0.9121897290825783
print(x[0][0][0][0])  # 0.9121897290825783

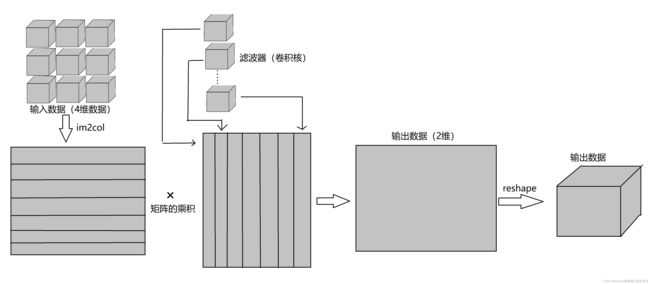
2，基于im2col的展开：

CNN中处理4维数组时，卷积运算会很复杂，可能是使用for循环去遍历，但是，通过使用im2col这个技巧就会把问题变得简单

im2col是一个函数，能将输入数据展开成适合卷积核的形状；im2col的意思是 “image to cn （图像到矩阵的意思）”的缩写。Caffe、Chainer等深度学习框架中有名为im2col的函数，也在卷积层上广泛使用；

如图例：对于输入3维数据，im2col将他按行方向转换成2维矩阵

 在实际的卷积运算中，卷积核的应用区域几乎是重叠的，使用im2col展开后，元素的个数会多于原方块元素个数。因此，使用im2col的实现存在比普通的实现消耗内存更大的缺点；

如图，使用im2col函数展开输入数据后，之后就只需要将卷积层的滤波器纵向展开成1列，并计算2个矩阵的乘积。这和 全连接神经网络的Affine层进行处理的原理相同。再将2维数组转变成4维数组，这就是卷积层的实现流程。

im2col函数的代码：im2col会考虑卷积核的大小、步幅、填充、将输入数据展开成2维数据。

def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    """

    Parameters
    ----------
    input_data : 由(数据量, 通道, 高, 长)的4维数组构成的输入数据
    filter_h : 滤波器的高
    filter_w : 滤波器的长
    stride : 步幅
    pad : 填充

    Returns
    -------
    col : 2维数组
    """
    N, C, H, W = input_data.shape
    out_h = (H + 2 * pad - filter_h) // stride + 1
    out_w = (W + 2 * pad - filter_w) // stride + 1

    img = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))

    for y in range(filter_h):
        y_max = y + stride * out_h
        for x in range(filter_w):
            x_max = x + stride * out_w
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]

    col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
    return col

 观察这俩例子：批大小为1时，保存的数据是(576, 25)；批大小为10时，保存的数据是(5760, 25) 

import numpy as np

x = np.random.rand(1, 1, 28, 28)
x2 = np.random.rand(10, 1, 28, 28)


def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
    N, C, H, W = input_data.shape
    out_h = (H + 2 * pad - filter_h) // stride + 1
    out_w = (W + 2 * pad - filter_w) // stride + 1

    img = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))

    for y in range(filter_h):
        y_max = y + stride * out_h
        for x in range(filter_w):
            x_max = x + stride * out_w
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]

    col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_h * out_w, -1)
    return col


print(im2col(x, 5, 5, stride=1, pad=0).shape)  # (576, 25)
print(im2col(x2, 5, 5, stride=1, pad=0).shape)  # (5760, 25)

3，卷积层的实现：

利用im2col实现卷积层的正向传播，其反向传播当然是使用col2im函数；

col2im函数代码：

def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
    """

    Parameters
    ----------
    col :
    input_shape : 输入数据的形状（例：(10, 1, 28, 28)）
    filter_h :
    filter_w
    stride
    pad

    Returns
    -------

    """
    N, C, H, W = input_shape
    out_h = (H + 2 * pad - filter_h) // stride + 1
    out_w = (W + 2 * pad - filter_w) // stride + 1
    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)

    img = np.zeros((N, C, H + 2 * pad + stride - 1, W + 2 * pad + stride - 1))
    for y in range(filter_h):
        y_max = y + stride * out_h
        for x in range(filter_w):
            x_max = x + stride * out_w
            img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]

    return img[:, :, pad:H + pad, pad:W + pad]

卷积层代码 ：

forward中，transpose函数会更改多维数组的轴的顺序：

import numpy as np

x1 = np.arange(0, 16).reshape(2, 2, 2, 2)
print(x1)
print("--------------------------------")
print(x1.transpose(0, 3, 1, 2))

[[[[ 0  1]
   [ 2  3]]

  [[ 4  5]
   [ 6  7]]]

 [[[ 8  9]
   [10 11]]

  [[12 13]
   [14 15]]]]
--------------------------------
[[[[ 0  2]
   [ 4  6]]

  [[ 1  3]
   [ 5  7]]]

 [[[ 8 10]
   [12 14]]

  [[ 9 11]
   [13 15]]]]

Process finished with exit code 0
 

class Convolution:
    def __int__(self, w, b, stride=1, pad=0):
        self.w = w
        self.b = b
        self.stride = stride
        self.pad = pad

        self.x = None
        self.col = None
        self.col_w = None

        self.dw = None
        self.db = None

    def forward(self, x):
        FN, C, FH, FW = self.w.shape
        N, C, H, W = x.shape
        out_h = int(1 + (H + 2 * self.pad - FH) / self.stride)
        out_w = int(1 + (W + 2 * self.pad - FW) / self.stride)

        col = im2col(x, FH, FW, self.stride, self.pad)
        col_w = self.w.reshpae(FN, -1).T
        out = np.dot(col, col_w) + self.b
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

        return out

    def backward(self, dout):
        FN, C, FH, FW = self.w.shape
        dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)

        self.db = np.sum(dout, axis=0)
        self.dw = np.dot(self.col.T, dout)
        self.dw = self.dw.transpose(1, 0).reshape(FN, C, FH, FW)

        dcol = np.dot(dout, self.col_w.T)
        dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)

        return dx

4，池化层的实现：

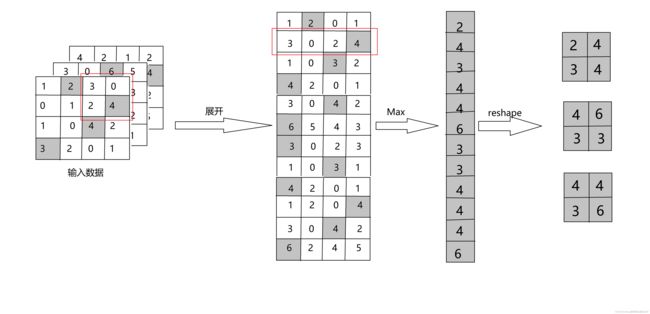
池化层和卷积层一样，也是使用im2col函数对输入数据展开。由于池化层通道数不会改变，在各个通道上是独立的，即池化的应用区域按通道单独展开；展开后，只需要对展开的矩阵求各行最大值，并转换为合适形状即可。

如图所示，池化层的实现只需要3个阶段：

1，展开输入数据；2，求个行的最大值；3，转换为适合的输出大小； 

池化层代码： 

class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad
        
        self.x = None
        self.arg_max = None

    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)

        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
        col = col.reshape(-1, self.pool_h*self.pool_w)

        arg_max = np.argmax(col, axis=1)
        out = np.max(col, axis=1)
        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)

        self.x = x
        self.arg_max = arg_max

        return out

    def backward(self, dout):
        dout = dout.transpose(0, 2, 3, 1)
        
        pool_size = self.pool_h * self.pool_w
        dmax = np.zeros((dout.size, pool_size))
        dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
        dmax = dmax.reshape(dout.shape + (pool_size,)) 
        
        dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
        dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
        
        return dx

最大值计算是利用了，Numpy库的np.max()函数，其能指定axis= 参数，并在这个参数指定的各个方向上求最大值。