数据结构：带环单链表基础OJ练习笔记(leetcode142. 环形链表 II)(leetcode三题大串烧)

目录

一.前言 

二.leetcode160. 相交链表 

1.问题描述

2.问题分析与求解

三.leetcode141. 环形链表

1.问题描述

2.代码思路 

3.证明分析 

下一题会用到的重要小结论：

四.leetcode142. 环形链表 II

1.问题描述

2.问题分析与求解

Judgecycle接口：

方法一：

方法二： 

---

一.前言 

单链表和带环单链表OJ题是笔试面试常考的题目,本期是关于带环单链表基础题的刷题小笔记(前两个题的求解过程可以用于求解第三个题哦!)

二.leetcode160. 相交链表 

leetcode链接：160. 相交链表 - 力扣（Leetcode）

1.问题描述

给你两个单链表的头节点的地址 headA 和 headB ，请你找出并返回两个单链表相交部分的起始节点。如果两个链表不存在相交节点，返回 null 。

比如图示两个链表：

已知a1和b1的地址,编写程序返回c1的地址。

• 测试用例中的链表不存在环
• 函数返回结果后，两个链表必须保持其原始结构 

题解接口：

class Solution 
{
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) 
    {
        
    }
};

2.问题分析与求解

方法一:

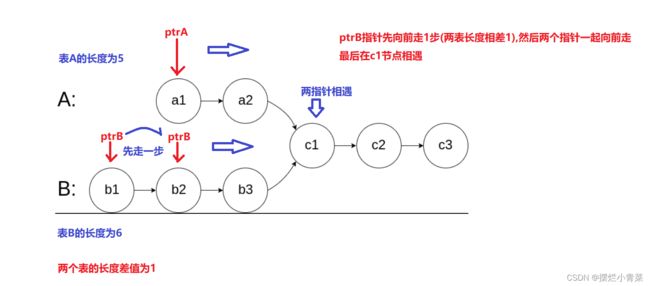
• 先各自求出两个链表的长度,并求出它们长度的差值：

• 然后再用两个指针来分别遍历两个链表,其中遍历较长链表的指针要先向前走N步(N表示两个链表长度的差值),然后两个指针再一起向前遍历两个链表,若链表存在交点,则两个指针必定会在交点相遇：

题解代码：

class Solution 
{
public:
    int countNode(ListNode * head)   //封装一个求节点个数的函数
    {
        int count = 0;
        while(head)
        {
            count++;
            head=head->next;
        }
        return count;
    }
    ListNode * foundNode(ListNode* longlist,ListNode* shortlist,int diff)
    //封装一个求第一个相交节点的函数
    {
        while(diff)                   //遍历长链表的指针先向前走diff步
        {
            longlist = longlist->next;
            --diff;
        }
        while(longlist && shortlist)  //两指针一起向前走直到相遇或指向空指针
        {
            if(longlist == shortlist)
            {
                return longlist;
            }
            longlist=longlist->next;
            shortlist=shortlist->next;
        }
        return nullptr;               //最终指向空指针则说明两表不相交
    }
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) 
    {
        int countA = countNode(headA);
        int countB = countNode(headB);
        if(countA>=countB)
        {
            return foundNode(headA,headB,countA-countB);
        }
        else
        {
            return foundNode(headB,headA,countB-countA);
        }
    }
};

这个方法思路比较简单但是不够简洁优雅,还有一个更简洁优雅的解法。

方法二：

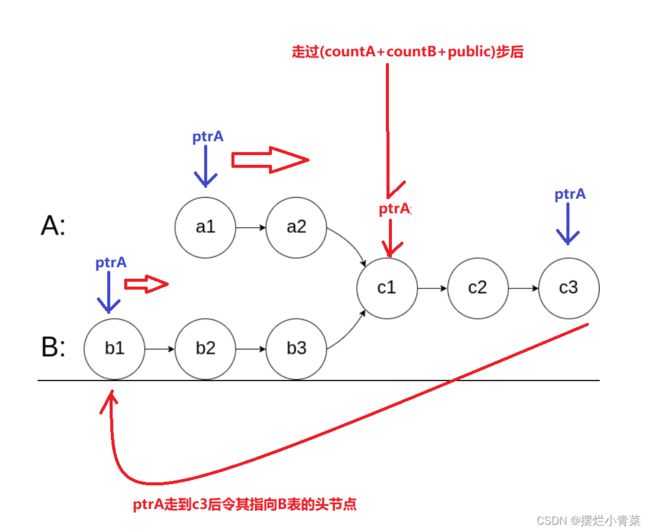
• 我们先考虑遍历表A的指针：当遍历表A的指针走到尾节点后,我们令其返回指向表B的头节点,此后如果该指针继续向前走countB步,则指针会来到两个链表的第一个相交节点，此时遍历表A的指针总共向前走了(countA + public + countB)次,如图：
• 类似地,遍历B表的指针走到表尾后,我们令其返回指向表A的头节点,此后如果该指针再向前走countA步则同样会来到两表的第一个相交节点.此时遍历B表的指针同样总共向前走了(countA+countB+public)次.
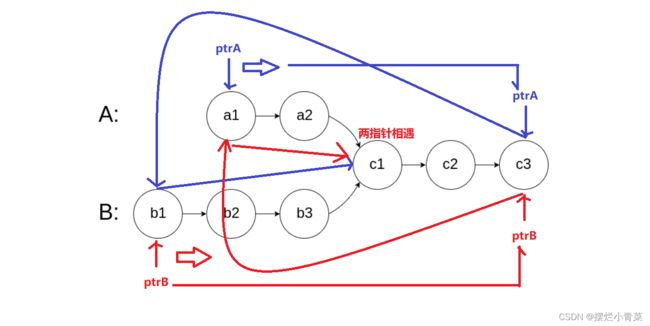
• 因此如果我们让遍历表A和表B的指针同时向前遍历链表,当他们走到表尾后,则令他们返回指向另外一个链表的头节点,两指针最终必定会在两链表第一个相交节点相遇(此时两个指针同时向前走了(countA + countB + public)次)。如图:

题解代码：

class Solution 
{
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) 
    {
        ListNode * ptrA = headA;
        ListNode * ptrB = headB;
        while(ptrA!=ptrB)
        {
            ptrA = (ptrA==nullptr)? headB : ptrA->next; //(ptrA==nullptr)代表指针指向A表尾
            ptrB = (ptrB==nullptr)? headA : ptrB->next; //(ptrB==nullptr)代表指针指向B表尾
        }
        return ptrA;
    }
};

•  若两个链表不相交,最终两个指针会同时变为空指针,函数会返回空指针

三.leetcode141. 环形链表

141. 环形链表 - 力扣（Leetcode）

1.问题描述

给你一个链表的头节点的地址head ，判断链表中是否有环。

(如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环.)

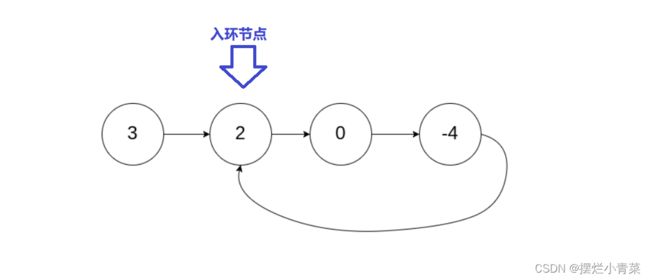
如果链表中存在环 ，则返回 true 。 否则，返回 false 。

比如：

题解接口：

class Solution 
{
public:
    bool hasCycle(ListNode *head) 
    {
        
    }
};

2.代码思路 

本题的代码思路很简单,利用的是快慢指针法,两个指针同时遍历链表,快指针一次走两步,慢指针一次走一步。

• 如果链表中不存在环,则快指针会率先达到表尾。
• 如果链表中存在环,则快慢指针最终会在环中相遇。

题解代码：

class Solution 
{
public:
    bool hasCycle(ListNode *head) 
    {
        if(nullptr == head || nullptr == head->next)//单节点和无节点链表做额外判断
        {
            return false;
        }
        ListNode* fast = head->next->next; //让快指针先走两步,慢指针走一步让它们指向不同节点
        ListNode* slow = head->next;
        while((fast && fast->next && fast!=slow))
        {
            fast=fast->next->next;         //快指针一次走两步
            slow=slow->next;               //慢指针一次走一步
        }
        return (fast==slow)? true : false; //判断两指针是否相遇并确定返回值(若无环fast一定不等 
                                           //slow)
    }
};

然而本题的关键并不在于代码如何写,而是在于如何去证明上述求解思路的合理性。

接下来我们尝试对快慢指针法在本题中的合理性做一个比较严格的证明。

3.证明分析 

下文的所谓的距离指的是两个链表节点位置之间指针链的数目。

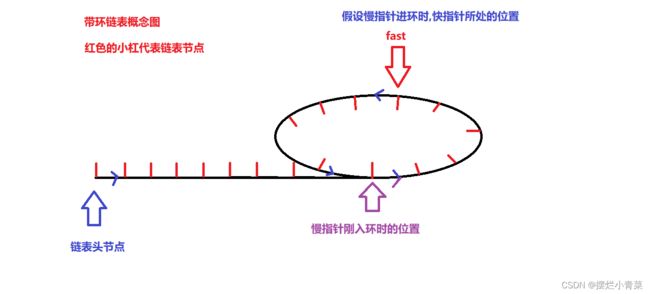
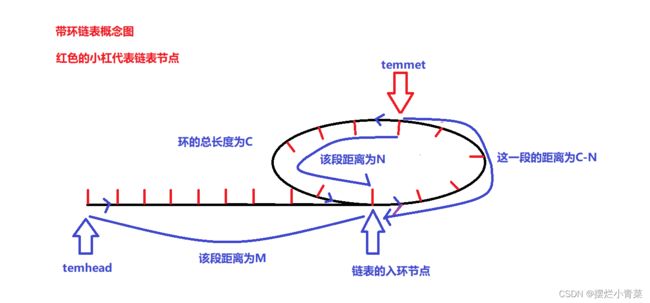
• 我们先将带环链表用一个概念图表示一下： 
•  我们令快慢指针同时从链表头节点出发：(fast=fast->next->next表示快指针一次走两步)(slow=slow->next表示慢指针一次走一步)
• 如果链表中不存在环,易知快指针fast必然率先结束遍历链表的过程(fast或fast->next指向空),此时返回false。
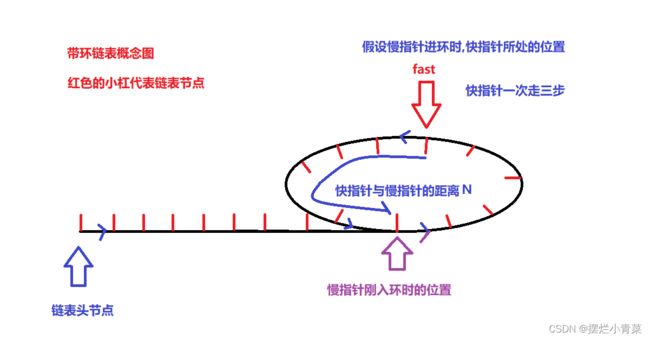
• 如果链表中存在环,那么快指针会率先进环,之后慢指针入环时,快指针此时一定处于环中某个位置:
• 此后快指针开始在环中追赶慢指针,假设慢指针入环时,快指针与慢指针的距离为N(N小于或等于环的总长度减一)(N为某一个正整数)
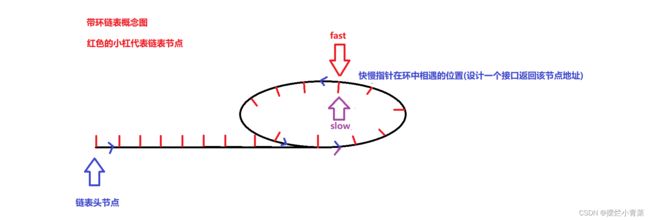
• 慢指针入环时两指针的环上距离是整数N.快指针每次循环前进两步,慢指针每次循环前进一步,可知两个指针的距离每次循环后会缩小1,则快指针必定会在环上某个点与慢指针相遇(即fast==slow，此时说明链表中存在环)

---

下一题会用到的重要小结论：

• 另外还有一个重要小结论：快慢指针相遇时,慢指针在环上走过的距离一定小于环的长度(因为N小于或等于环的总长度减一) (该结论在下一题中会用到)

更进一步的思考：如果快指针一次走三步或者n步(n>2),慢指针仍然一次走一步,那么是否还能确保快慢指针一定会在环中相遇？

• 答案是否定的,我们可以规定让快指针一次走三步来做一下分析,设当慢指针刚入环时,两个指针的距离为N：
• 快指针一次走三步,那么每次循环两个指针的距离会缩小2
• 假如N是偶数,那么快指针最终会与慢指针相遇
• 假如N是奇数,那么快指针追上慢指针后会处于慢指针的前一个位置。(整除余1)
• 此时快指针重新开始追赶慢指针:设环的长度为X,则此时相当于快指针与慢指针的距离为X-1
• 若X-1为偶数,那么快指针最终可以与慢指针相遇
• 若X-1为奇数,那么快指针追上慢指针后会又一次处于慢指针的前一个位置。紧接着就开始了无限循环追赶,两个指针永远都不会相遇
• 同样地,若令快指针一次走3,4,5...n步,通过数学归纳思维,我们同样能分析出(在各种不同的环长度的链表中)可能会出现和上述类似的无限追赶的情况,因此可以得出结论:快指针每次必须比慢指针多走1步才能确保(在任何带环链表中)两指针最终会在环中会相遇。

四.leetcode142. 环形链表 II

142. 环形链表 II - 力扣（Leetcode）

1.问题描述

该题在上一题的基础上,要求我们编写的接口能够返回链表开始入环的第一个节点的地址。如果链表无环，则返回 nullptr.

比如：

题解接口：

class Solution
{
public:
    ListNode* detectCycle(ListNode* head)
    {
        
    }
};

2.问题分析与求解

第一步：

本题的求解建立在上一个题目的基础之上.

我们先编写一个额外的Judgecycle接口,用于判断链表是否带环,并且返回快慢指针在环中相遇位置节点的地址(链表不带环则返回空指针)。

Judgecycle接口：

    ListNode* Judgecycle(ListNode* head)
    {
        if(nullptr==head || nullptr == head->next)
        {
            return nullptr;
        }
        ListNode *fast =head->next->next;
        ListNode *slow = head->next;
        while(fast && fast->next && fast!=slow)
        {
            fast=fast->next->next;
            slow = slow ->next;
        }
        return (fast&&fast->next)? fast : nullptr;//(fast或fast->next为空则表示链表无环)
    }                                             //(为空说明fast走到表尾)  

• 若链表带环,返回的fast指针就是快慢指针在环中相遇的位置的节点的地址
• 该接口的原理参见上一题的分析。
• 在题解接口中我们用一个temmet指针来接收Judgecycle接口的返回值

   
  
  class Solution
  {
  public:
      ListNode* Judgecycle(ListNode* head)
      {
          if(nullptr==head || nullptr == head->next)
          {
              return nullptr;
          }
          ListNode *fast =head->next->next;
          ListNode *slow = head->next;
          while(fast && fast->next && fast!=slow)
          {
              fast=fast->next->next;
              slow = slow ->next;
          }
          return (fast&&fast->next)? fast : nullptr;//(fast或fast->next为空则表示链表无环)
      }                                             //(为空说明fast走到表尾)
  
  
                                               
      ListNode* detectCycle(ListNode* head)         //题解接口
      {
         ListNode * temmet = Judgecycle(head);
         ListNode* temhead = head;
         //其他操作步骤
      }
  };                                             

基于上面的Judgecycle接口,接下来我们有两种方法可以求解本题

方法一：

• 假设环中temmet指针(指向Judgecycle接口中快慢指针在环中相遇位置节点)与环入口节点的距离为N
• 假设链表头节点与环入口节点的距离为M
• 假设环的总长度(距离)为C(不包括M)

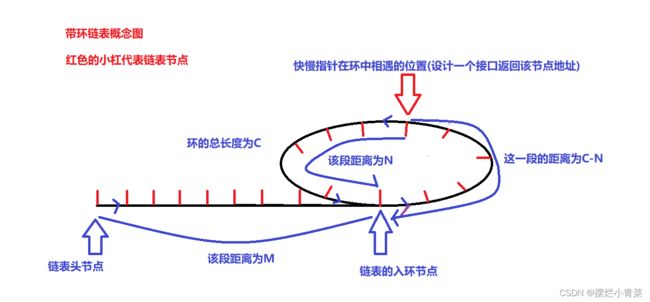
接着我们来分析N,M,C之间存在着什么样的数学关系.

利用前一个题的一个重要结论(见目录)：Judgecycle接口中快慢指针相遇时,慢指针在环上走过的距离一定小于环的长度

• 于是：在Judgecycle接口中,快慢指针相遇时慢指针在链表中走过的总距离为(M+C-N)
• 进一步可以得出,快慢指针相遇时快指针在链表中走过的总距离为2*(M+C-N)
• 假设快慢指针相遇时,快指针已经在环中走了n圈，那么我们便可以用另外一种方式表示出快慢指针相遇时快指针在链表中走过的总距离：M+n*C+(C-N)
• 于是得到方程：2*(M+C-N)=M+n*C+(C-N)
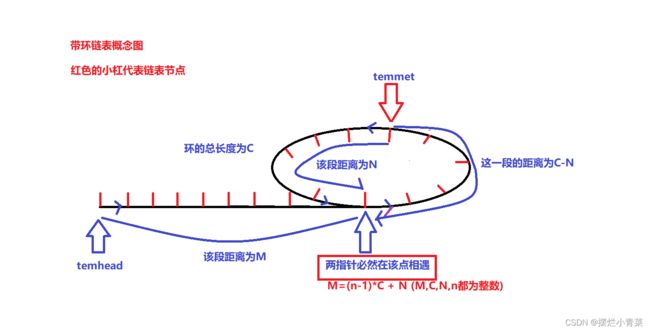
• 化简可得：M+C-N = n*C 即：M=(n-1)*C + N  (M,C,N,n都为整数)
• 令一个指针temhead初始位置指向链表头节点,另外一个指针temmet初始位置指向环中快慢指针相遇的位置(由Judgecycle接口返回)
• 两个指针同时开始遍历链表,根据关系式M=(n-1)*C + N (M,C,N,n都为整数)可知两个指针必然在链表的入环节点相遇。返回指针的值即可得到答案。

      ListNode* detectCycle(ListNode* head)
      {
          ListNode* temmet = Judgecycle(head);      //快慢指针相遇位置节点的地址
          ListNode* temhead = head;
          if (temmet) //判断temmet是否为空,为空说明链表不带环
          {
              while (temhead != temmet)             //两个指针同时向前遍历链表直到相遇
              {
                  temmet = temmet->next;
                  temhead = temhead->next;
              }
              return temmet;                        //返回相遇位置节点地址
          }
          return nullptr;      //代表链表无环
      }

  

题解代码：

class Solution
{
public:
    ListNode* Judgecycle(ListNode* head)
    {
        if(nullptr==head || nullptr == head->next)
        {
            return nullptr;
        }
        ListNode *fast =head->next->next;
        ListNode *slow = head->next;
        while(fast && fast->next && fast!=slow)
        {
            fast=fast->next->next;
            slow = slow ->next;
        }
        return (fast&&fast->next)? fast : nullptr;//(fast或fast->next为空则表示链表无环)
    }                                             //(为空说明fast走到表尾)   

    ListNode* detectCycle(ListNode* head)
    {
        ListNode* temmet = Judgecycle(head);      //快慢指针相遇位置节点的地址
        ListNode* temhead = head;
        if (temmet) //判断temmet是否为空,为空说明链表不带环
        {
            while (temhead != temmet)             //两个指针同时向前遍历链表直到相遇
            {
                temmet = temmet->next;
                temhead = temhead->next;
            }
            return temmet;                        //返回相遇位置节点地址
        }
        return nullptr;      //代表链表无环
    }
};

方法二： 

• 确定了Judgecycle接口中快慢指针在环中相遇的位置后,我们在两指针相遇的节点处将环断开
• 于是问题就转换成了求两个相交链表第一个相交节点地址的问题(问题求解参见本期第一个OJ题) ,其中快慢指针在环中相遇位置的节点作为断环后新链表的头节点

因此我们可以调用前两个题的接口来求解本题：

class Solution
{
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)                        
    //求相交链表第一个交点的接口
    {
        ListNode * ptrA = headA;
        ListNode * ptrB = headB;
        while(ptrA!=ptrB)
        {
            ptrA = (ptrA==nullptr)? headB : ptrA->next; //(ptrA==nullptr)代表指针指向A表尾
            ptrB = (ptrB==nullptr)? headA : ptrB->next; //(ptrB==nullptr)代表指针指向B表尾
        }
        return ptrA;
    }
public:
    ListNode* Judgecycle(ListNode* head)          //求快慢指针在环中相遇位置的接口
    {
        if(nullptr==head || nullptr == head->next)
        {
            return nullptr;
        }
        ListNode *fast =head->next->next;
        ListNode *slow = head->next;
        while(fast && fast->next && fast!=slow)
        {
            fast=fast->next->next;
            slow = slow ->next;
        }
        return (fast&&fast->next)? fast : nullptr;//(fast或fast->next为空则表示链表无环)
    }                                             //(为空说明fast走到表尾)   

    ListNode* detectCycle(ListNode* head)
    {
        ListNode* temmet = Judgecycle(head);
        if (temmet)                                 //判断temmet是否为空,为空说明链表不带环
        {
            ListNode* breakpoint = temmet;
            while(breakpoint->next != temmet)       //找到环中的断开点
            {
                breakpoint = breakpoint->next; 
            }
            breakpoint->next = nullptr;             //将环断开
            return getIntersectionNode(temmet,head);//转化为求两链表第一个交点的问题
        }
        return nullptr;                             //代表链表无环
    }
};

• 根据我们上面各步骤的分析不难得出两种求解方法的时间复杂度都是O(N),但是方法一会比方法二略高效一些。