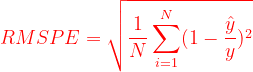07- Rossmann商店销售预测 (Xgboost集成算法) (项目七)
- 查看数据是否为空: train.isnull().sum()
- 查看特征元素: train['StateHoliday'].unique() # array(['0', 'a', 'b', 'c'], dtype=object)
- 绘制热力图: sns.heatmap(df_train.corr(),cmap = 'RdYlGn_r',annot=True,vmin = -1,vmax=1)
- 合并商店信息和销售数据: train = pd.merge(train, store, on = 'Store', how = 'left')
- 画柱状图: _ = plt.hist(y_train,bins = 100)
- 保存模型: gbm.save_model('./train_model.json')
- 查看预测值发现整体偏高, 集体调整.
- Xgboost模型训练:
params = {'objective':'reg:linear',
'booster':'gbtree',
'eta':0.03,
'max_depth':10,
'subsample':0.9,
'colsample_bytree':0.7,
'silent':1,
'seed':10}
num_boost_round = 6000
dtrain = xgb.DMatrix(X_train,y_train)
dtest = xgb.DMatrix(X_test,y_test) # 保留的验证数据
print('模型训练开始……')
evals = [(dtrain,'train'),(dtest,'validation')]
gbm = xgb.train(params,# 模型参数
dtrain, # 训练数据
num_boost_round, # 轮次,决策树的个数
evals = evals,# 验证,评估的数据
early_stopping_rounds=100, # 在验证集上,当连续n次迭代,分数没有提高后终止训练
feval=rmspe_xg,# 模型评估的函数
verbose_eval=True)# 打印输出log日志,每次训练详情1、项目的背景与目的
使用商店、促销和竞争对手数据预测销售Rossmann在欧洲国家经营着3000多家日化用品超市。目前,Rossmann商店经理的任务是提前6周预测他们的日销售额。商店的销售受到许多因素的影响,包括促销、竞争、学校和国家假日、季节性和地域性。由于数以千计的管理者根据自己的特殊情况预测销售,结果的准确性可能会有很大的差异。
因此使用机器学习算法对销量进行预测,Rossmann要求预测德国1115家商店的6周日销售额。可靠的销售预测使商店经理能够制定有效的员工时间表,提高生产力和积极性。
这就是算法和零售、物流领域的一次深度融合,从而提前备货,减少库存、提升资金流转率,促进公司更加健康发展,为员工更合理的工作、休息提供合理安排,为工作效率提高保驾护航。
2、数据介绍
- train.csv - 包含销售情况的历史数据文件
- test.csv - 不包含销售情况的历史数据文件
- sample_submission.csv - 数据提交样本文件
- store.csv - 商店更多信息文件
字段说明
Store: 每个商店唯一的ID
Sales: 销售额
Customers: 销售客户数
Open: 商店是否营业 0=关闭,1=开业
StateHoliday: 国家假日
SchoolHoliday: 学校假期
StoreType 店铺类型: a, b, c, d
Assortment 产品组合级别: a = 基本, b = 附加, c = 扩展
CompetitionDistance: 距离最近的竞争对手距离(米)
CompetitionOpenSince[Month/Year]: 最近的竞争对手开业时间
Promo: 指店铺当日是否在进行促销
Promo2: 指店铺是否在进行连续促销 0 = 未参与, 1 = 正在参与
Promo2Since[Year/Week]: 商店开始参与Promo2的时间
PromoInterval: 促销期
StateHoliday:通常所有商店都在国家假日关门:a = 公共假日, b = 复活节假日,c = 圣诞节,0= 无
3、数据加载
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import xgboost as xgb
import time3.1、查看数据
# 加载数据时,为特定字段指定了数据类型
train = pd.read_csv('./data/train.csv',dtype={'StateHoliday':np.string_})
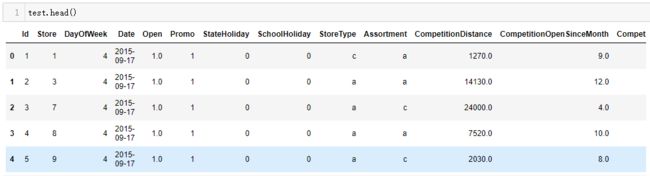
test = pd.read_csv('./data/test.csv',dtype={'StateHoliday':np.string_})
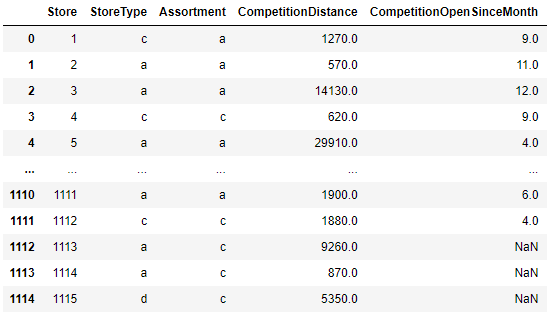
store = pd.read_csv('./data/store.csv') # 每个店铺的详情
display(train.head(),test.head(),store.head())
print(train.shape,test.shape,store.shape) # (1017209, 9) (41088, 8) (1115, 10)- 数据中存在空数据,一次需要处理空数据
3.2.1、训练数据处理
train.isnull().sum() - 表明train这个数据中没有空数据
3.2.2、测试数据处理
test.isnull().sum()cond = train['Store'] == 622
df = train[cond]
df.sort_values(by = 'Date').iloc[-50:] # 根据过往的数据,对测试数据中622号店铺进行填充
# 原来大部分情况,622都是营业!test.fillna(1,inplace=True) # 填充空数据
test.isnull().sum()- 填充空数据
3.3.3、商店数据处理
store.isnull().sum()v1 = 'CompetitionDistance'
v2 = 'CompetitionOpenSinceMonth'
v3 = 'CompetitionOpenSinceYear'
v4 = 'Promo2SinceWeek'
v5 = 'Promo2SinceYear'
v6 = 'PromoInterval'# v2和v3 同时缺失
store[(store[v2].isnull()) & (store[v3].isnull())].shape
'''(354, 10)''' # v4、v5、v6同时缺失
store[(store[v4].isnull())&(store[v5].isnull())&(store[v6].isnull())].shape
'''(544, 10)'''- 下面对缺失数据进行填充。
- 店铺竞争数据缺失,而且缺失的都是对应的。
- 原因不明,而且数量也比较多,如果用中值或均值来填充,有失偏颇。暂且填0,解释意义就是刚开业。
- 店铺促销信息的缺失是因为没有参加促销活动,所以我们以0填充。
3.3.4、商店数据填充
store.fillna(0,inplace=True) # 填充成,解释含义:刚开业
store.isnull().sum()3.3.5、销量时间关系
cond = train['Sales'] > 0
sales_data = train[cond] # 获取销售额为正的数据
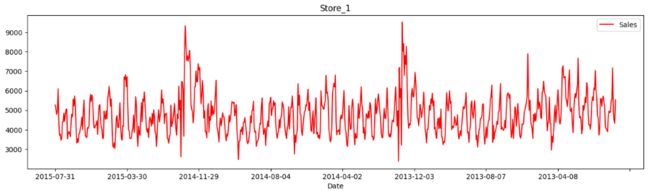
sales_data.loc[train['Store'] == 1].plot(x = 'Date',y = 'Sales',
title = 'Store_1',
figsize = (16,4),color = 'red')test['Date'].unique() # 测试数据,要预测8~9月份的销售情况
'''array(['2015-09-17', '2015-09-16', '2015-09-15', '2015-09-14',
'2015-09-13', '2015-09-12', '2015-09-11', '2015-09-10',
'2015-09-09', '2015-09-08', '2015-09-07', '2015-09-06',
'2015-09-05', '2015-09-04', '2015-09-03', '2015-09-02',
'2015-09-01', '2015-08-31', '2015-08-30', '2015-08-29',
'2015-08-28', '2015-08-27', '2015-08-26', '2015-08-25',
'2015-08-24', '2015-08-23', '2015-08-22', '2015-08-21',
'2015-08-20', '2015-08-19', '2015-08-18', '2015-08-17',
'2015-08-16', '2015-08-15', '2015-08-14', '2015-08-13',
'2015-08-12', '2015-08-11', '2015-08-10', '2015-08-09',
'2015-08-08', '2015-08-07', '2015-08-06', '2015-08-05',
'2015-08-04', '2015-08-03', '2015-08-02', '2015-08-01'],
dtype=object)'''- 从图中可以看出店铺的销售额是有周期性变化的,一年中11,12月份销量相对较高,可能是季节(圣诞节)因素或者促销等原因。
- 此外从2014年6-9月份的销量来看,6,7月份的销售趋势与8,9月份类似,而我们需要预测的6周在2015年8,9月份,因此我们可以把2015年6,7月份最近6周的1115家店的数据留出作为测试数据,用于模型的优化和验证!
4、合并数据 (商店数据和店铺数据)
display(train.shape,test.shape)
cond = train['Sales'] > 0
train = train[cond] # 过滤了销售额小于0的数据
train = pd.merge(train,store,on = 'Store',how = 'left')
test = pd.merge(test,store,on = 'Store',how = 'left')
display(train.shape,test.shape)
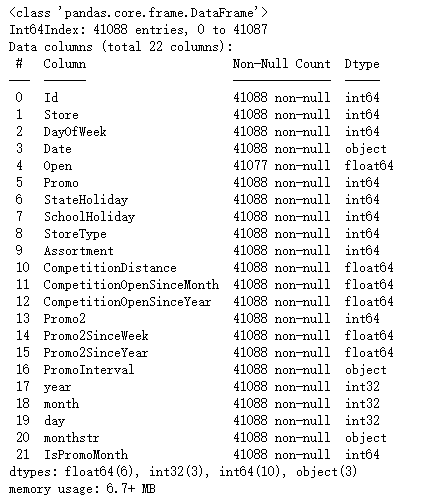
'''(1017209, 9) (41088, 8) (844338, 18) (41088, 17)'''train.info()5、特征工程
train['StateHoliday'].unique() # array(['0', 'a', 'b', 'c'], dtype=object)%%time
for data in [train,test]:
# 修改时间
data['year'] = data['Date'].apply(lambda x : x.split('-')[0]).astype(int)
data['month'] = data['Date'].apply(lambda x : x.split('-')[1]).astype(int)
data['day'] = data['Date'].apply(lambda x : x.split('-')[2]).astype(int)
# 店铺有一个字段:PromoInterval,string类型,无法进行建模
# IsPromoMonth 是否进行了促销
month2str = {1:'Jan',2:'Feb',3:'Mar',4:'Apr',5:'May',6:'Jun',7:'Jul',8:'Aug',
9:'Sep',10:'Oct',11:'Nov',12:'Dec'}
data['monthstr'] = data['month'].map(month2str)
# convert是转换函数
convert = lambda x : 0 if x['PromoInterval'] == 0 else 1 if x['monthstr'] in x['PromoInterval'] else 0
# 这个月是否为促销月
data['IsPromoMonth'] = data.apply(convert,axis = 1)
# 将存在字符串类型转换成数字:StoreType、Assortment、StateHoliday
mappings = {'0':0,'a':1,'b':2,'c':3,'d':4}
data['StoreType'].replace(mappings,inplace = True)
data['Assortment'].replace(mappings,inplace = True)
data['StateHoliday'].replace(mappings,inplace = True)train['StoreType'].unique() # array([3, 1, 4, 2], dtype=int64)
train['Assortment'].unique() # array([1, 3, 2], dtype=int64)
train['StateHoliday'].unique() # array([0, 1, 2, 3], dtype=int64)
test.info()6、构建训练数据和测试数据
display(train.shape,test.shape) # (844338, 23) (41088, 22)
df_train=train.drop(['Date','monthstr','PromoInterval','Customers','Open'],axis=1)
df_test = test.drop(['Date','monthstr','PromoInterval','Open','Id'],axis = 1)
display(df_train.shape,df_test.shape) # (844338, 18) (41088, 17)train[:6*7*1115]['Date'].unique()
'''array(['2015-07-31', '2015-07-30', '2015-07-29', '2015-07-28',
'2015-07-27', '2015-07-26', '2015-07-25', '2015-07-24',
'2015-07-23', '2015-07-22', '2015-07-21', '2015-07-20',
'2015-07-19', '2015-07-18', '2015-07-17', '2015-07-16',
'2015-07-15', '2015-07-14', '2015-07-13', '2015-07-12',
'2015-07-11', '2015-07-10', '2015-07-09', '2015-07-08',
'2015-07-07', '2015-07-06', '2015-07-05', '2015-07-04',
'2015-07-03', '2015-07-02', '2015-07-01', '2015-06-30',
'2015-06-29', '2015-06-28', '2015-06-27', '2015-06-26',
'2015-06-25', '2015-06-24', '2015-06-23', '2015-06-22',
'2015-06-21', '2015-06-20', '2015-06-19', '2015-06-18',
'2015-06-17', '2015-06-16', '2015-06-15', '2015-06-14',
'2015-06-13'], dtype=object)'''6.1 拆分训练数据
# df_train训练数据,历史数据
# 根据历史数据,进行建模,对df_test进行预测
# df_train这个数据,进行拆分:建模训练数据、验证数据(评估)
X_train = df_train[6*7*1115:] # 建模训练数据
X_test = df_train[:6*7*1115] # 建模验证数据(评估) 2015年 6~7月份的销售数据7、数据属性间相关性系数
plt.figure(figsize=(24,20))
plt.rcParams['font.size'] = 12
sns.heatmap(df_train.corr(),cmap = 'RdYlGn_r',annot=True,vmin = -1,vmax=1)8、提取模型训练的数据集
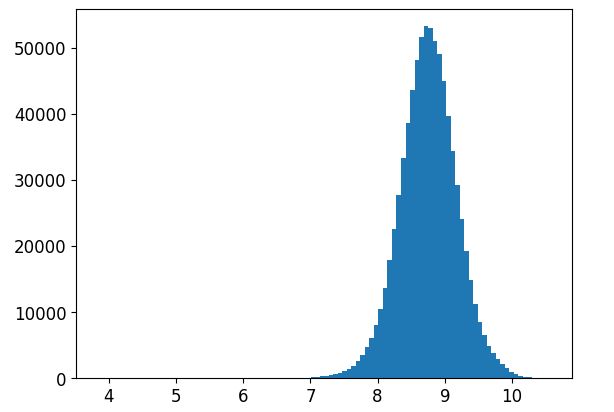
_ = plt.hist(X_train['Sales'],bins = 100) # 目标值,销售额,正态分布,不够正!!!8.1 数据正态化
# 目标值
y_train = np.log1p(X_train['Sales']) # 对数化
y_test = np.log1p(X_test['Sales']) # 对数化,正态化,更加规整,正态化
# 特征
X_train = X_train.drop('Sales',axis = 1) # X_train,y_train 数据--->目标值(建模)
X_test = X_test.drop('Sales',axis = 1) # X_test,y_test 数据 --->目标值(验证,评估)- 使用np.log1p进行对目标值处理,目标值更加正态化!
_ = plt.hist(y_train,bins = 100) 9、构建模型
9.1、定义评价函数
均方根百分比误差 :
def rmspe(y,yhat):
return np.sqrt(np.mean(1 - yhat/y)**2)
def rmspe_xg(y,yhat): # 放大镜
y = np.expm1(y)
yhat = np.expm1(yhat.get_label())# DMaxtrix数据类型,get_label获取数据
return 'rmspe',rmspe(y,yhat)x=[0,0.001,0.1,0.000001] # 举例
np.expm1(x) # expm1可以很好处理数字比较小的数组
# array([0.00000000e+00, 1.00050017e-03, 1.05170918e-01, 1.00000050e-06])9.2、模型训练
%%time
params = {'objective':'reg:linear',
'booster':'gbtree',
'eta':0.03,
'max_depth':10,
'subsample':0.9,
'colsample_bytree':0.7,
'silent':1,
'seed':10}
num_boost_round = 6000
dtrain = xgb.DMatrix(X_train,y_train)
dtest = xgb.DMatrix(X_test,y_test) # 保留的验证数据
print('模型训练开始……')
evals = [(dtrain,'train'),(dtest,'validation')]
gbm = xgb.train(params,# 模型参数
dtrain, # 训练数据
num_boost_round, # 轮次,决策树的个数
evals = evals,# 验证,评估的数据
early_stopping_rounds=100, # 在验证集上,当连续n次迭代,分数没有提高后终止训练
feval=rmspe_xg,# 模型评估的函数
verbose_eval=True)# 打印输出log日志,每次训练详情- 在XGBoost中数据的加载是使用其特有的数据格式进行训练的,我们可以使用XGBoost中的xgb.DMatrix(x_train, label=y_train)函数进行数据的加载,xgb.DMatrix()也支持libsvm格式的数据,这是一种稀疏数据的存储方式,xgb.DMatrix()可以直接读取这种数据格式 。
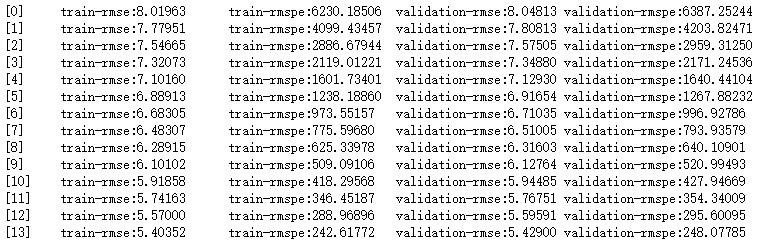
9.2.1、params参数说明
- eta: [默认是0.3] 和GBM中的learning rate参数类似。通过减少每一步的权重,可以提高模型的鲁棒性。典型值0.01-0.2
- max_depth: [默认是3] 树的最大深度,这个值也是用来避免过拟合的3-10
- subsample: [默认是1] 这个参数控制对于每棵树,随机采样的比例。减小这个参数的值算法会更加保守,避免过拟合。但是这个值设置的过小,它可能会导致欠拟合。典型值:0.5-1
- colsample_bytree: [默认是1] 用来控制每颗树随机采样的列数的占比每一列是一个特征0.5-1(要依据特征个数来判断)
seed: [默认是0]随机数的种子,设置它可以复现随机数据的结果,也可以用于调整参数。
booster: [默认是gbtree ]选择每次迭代的模型,有两种选择:gbtree基于树的模型、gbliner线性模型
silent: [默认值=0]取0时表示打印出运行时信息,取1时表示以缄默方式运行,不打印运行时信息。
objective: [默认是reg:linear]这个参数定义需要被最小化的损失函数。最常用的值有:
- binary,logistic二分类的逻辑回归,返回预测的概率非类别。multi:softmax使用softmax的多分类器,返回预测的类别。在这种情况下,你还要多设置一个参数:num_class类别数目。
- "reg:linear":线性回归。
- "reg:logistic":逻辑回归。
- "binary:logistic":二分类的逻辑回归问题,输出为概率。
- "binary:logitraw":二分类的逻辑回归问题,输出的结果为wTx。
- "count:poisson":计数问题的poisson回归,输出结果为poisson分布。在poisson回归中,max_delta_step的缺省值为0.7。(used to safeguard optimization)
- "multi:softmax":让XGBoost采用softmax目标函数处理多分类问题,同时需要设置参数num_class(类别个数)
- "multi:softprob":和softmax一样,但是输出是ndata * nclass的向量,可以将该向量reshape成ndata行nclass列的矩阵。没行数据表示样本所属于每个类别的概率。
- "rank:pairwise":set XGBoost to do ranking task by minimizing the pairwise loss
9.2.2、xgb.train()参数
params:这是一个字典,里面包含着训练中的参数关键字和对应的值
dtrain:训练的数据
num_boost_round:这是指提升迭代的次数,也就是生成多少基模型
evals:这是一个列表,用于对训练过程中进行评估列表中的元素。
feval: 自定义评估函数
early_stopping_rounds:早期停止次数 ,假设为100,验证集的误差迭代到一定程度在100次内不能再继续降低,就停止迭代。要求evals 里至少有 一个元素。
verbose_eval (布尔型或数值型):也要求evals 里至少有 一个元素。如果为True ,则对evals中元素的评估结果会输出在结果中;如果输入数字,假设为5,则每隔5个迭代输出一次
learning_rates:每一次提升的学习率的列表
xgb_model:在训练之前用于加载的xgb model
9.3、模型评估
print('验证数据表现:') # X_test就是验证数据
X_test.sort_index(inplace=True)
y_test.sort_index(inplace=True)
# 使用算法进行了预测
yhat = gbm.predict(xgb.DMatrix(X_test))
error = rmspe(np.expm1(y_test),np.expm1(yhat))
print('RMSPE:',error) # RMSPE: 0.0280719416230981# 画图查看,模型评估结果
res = pd.DataFrame(data = y_test) # 真实
res['Prediction'] = yhat # 预测
res = pd.merge(X_test,res,left_index=True,right_index=True)
res['Ratio'] = res['Prediction']/res['Sales'] # 预测和真实销量的比率
res['Error'] = abs(1 - res['Ratio']) # 误差率
res['weight'] = res['Sales']/res['Prediction'] # 真实销量占预测值的百分比
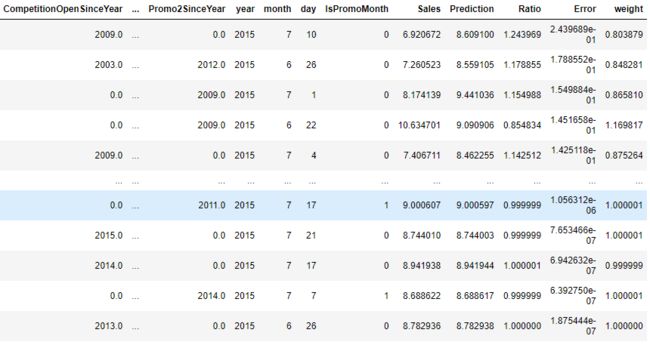
display(res.head())plt.rcParams['font.family'] = 'STKaiti'
col_1 = ['Sales','Prediction']
col_2 = ['Ratio']
# 随机选择三个店铺,进行可视化
shops = np.random.randint(1,1116,size = 3)
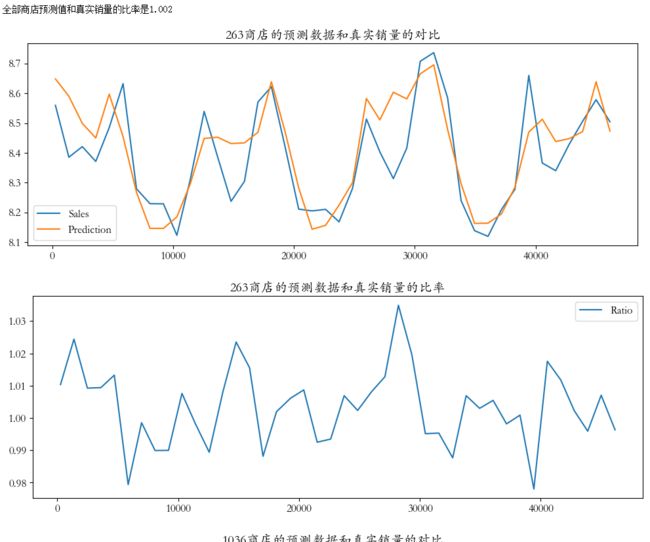
print('全部商店预测值和真实销量的比率是%0.3f' %(res['Ratio'].mean()))
for shop in shops:
cond = res['Store'] == shop
df1 = pd.DataFrame(data = res[cond],columns = col_1)
df2 = pd.DataFrame(data = res[cond],columns = col_2)
df1.plot(title = '%d商店的预测数据和真实销量的对比' % (shop),figsize = (12,4))
df2.plot(title = '%d商店的预测数据和真实销量的比率' % (shop),figsize = (12,4))# 偏差数据
res.sort_values(by = ['Error'],ascending=False)- 从分析结果来看,初始模型已经可以比较好的预测保留数据集的销售趋势,但相对真实值,模型的预测值整体要偏高一些。从对偏差数据分析来看,偏差最大的3个数据也是明显偏高。因此,我们可以以保留数据集为标准对模型进行偏差校正。
9.4、模型优化
weights = [(0.99 + (i/1000)) for i in range(20)]
errors = []
for w in weights:
# 偏差校正
error = rmspe(np.expm1(y_test),np.expm1(yhat * w))
# 这就是对预测值,进行权重乘法,微小改变
errors.append(error)
errors = pd.Series(errors,index=weights)
plt.figure(figsize=(9,6))
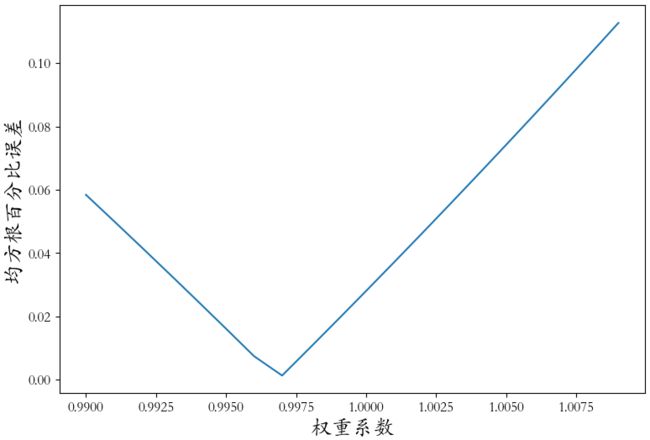
errors.plot()
plt.xlabel('权重系数',fontsize = 18)
plt.ylabel('均方根百分比误差',fontsize = 18)
index = errors.argmin()
print('最佳的偏差校正权重:',index,errors.iloc[7],weights[index])- 当校正系数为0.996时,保留数据集的RMSPE得分最低:0.125839。相对于初始模型0.129692得分有很大的提升。
- 因为每个店铺都有自己的特点,而我们设计的模型对不同的店铺偏差并不完全相同,所以我们需要根据不同的店铺进行一个细致的校正。
9.5、全局优化 (考虑不同店铺)
shops = np.arange(1,1116)
weights1 = [] # 验证数据每个店铺的权重系数 46830
weights2 = [] # 测试数据每个店铺的权重系数 41088,提交到Kaggle官网
for shop in shops:
cond = res['Store'] == shop
df1 = pd.DataFrame(res[cond], columns=col_1) # 验证数据的预测数据和真实销量
cond2 = df_test['Store'] == shop
df2 = pd.DataFrame(df_test[cond2])
weights = [(0.98 + (i/1000)) for i in range(40)]
errors = []
for w in weights:
error = rmspe(np.expm1(df1['Sales']),np.expm1(df1['Prediction'] * w))
errors.append(error)
errors = pd.Series(errors,index = weights)
index = errors.argmin() # 最小的索引
best_weight = np.array(weights[index]) # 只是一个数值
weights1.extend(best_weight.repeat(len(df1)).tolist())
weights2.extend(best_weight.repeat(len(df2)).tolist())
# for循环结束,每个店铺的权重,是多少,计算得到了
# 验证数据调整校正系数的排序
X_test = X_test.sort_values(by = 'Store') # 1,2,3,……1115
X_test['weights1'] = weights1 # 权重和店铺,进行一一对应!
X_test = X_test.sort_index() # 根据索引大小进行排序
weights1 = X_test['weights1']
X_test = X_test.drop('weights1',axis = 1)
# 测试数据调整校正系数
df_test = df_test.sort_values(by = 'Store') # 1,2,3,……1115
df_test['weights2'] = weights2 # 权重和店铺,进行一一对应!
df_test = df_test.sort_index() # 根据索引大小进行排序
weights2 = df_test['weights2']
df_test = df_test.drop('weights2',axis = 1)9.5.1 单个店铺分别加系数
set(weights1) '''{0.98,0.981,0.982,0.983,0.984,.....1.018, 1.019}'''
yhat_new = yhat * weights1 # 预测销售额,校正
rmspe(np.expm1(y_test),np.expm1(yhat_new))- RMSPE for weight corretion 0.118425,相对于整体校正的0.129692的得分又有不小的提高
9.6、模型预测
9.6.1 不经任何调整校正模型
# 使用算法,对测试数据,进行预测
test = xgb.DMatrix(df_test)
y_pred = gbm.predict(test) # 算法预测的结果,结果提交Kaggle
# y_pred 是对数运算的结果 真实数据,数据转换,幂运算
# 保存数据,不经任何调整校正
result = pd.DataFrame({'ID':np.arange(1,41089),'Sales':np.expm1(y_pred)})
result.to_csv('./result_1.csv',index=False)9.6.2 整体调整模型
# 对整体模型进行优化
w = 0.997
result = pd.DataFrame({'ID':np.arange(1,41089),'Sales':np.expm1(y_pred * w)})
result.to_csv('./result_2.csv',index=False)9.6.3 细致模型调整
# 进行更加细致的模型优化
weights2
# 每个店铺的,权重校正,都不同,细致!!!
result = pd.DataFrame({'ID':np.arange(1,41089),
'Sales':np.expm1(y_pred * weights2)})
result.to_csv('./result_3.csv',index=False)