机器学习经典算法总结

一，KNN 算法

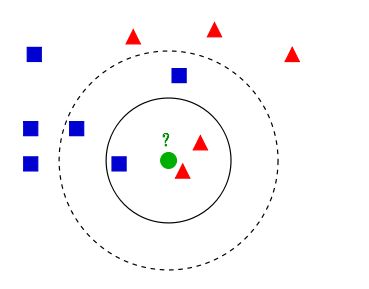
K 近邻算法（KNN）是一种基本分类和回归方法。KNN 算法的核心思想是如果一个样本在特征空间中的 k 个最相邻的样本中的大多数属于一个类别，那该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分类样本所属的类别。 如下图：

在 KNN 中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离，公式如下：

同时，KNN通过依据 k 个对象中占优的类别进行决策，而不是单一的对象类别决策，这两点就是KNN算法的优势。

1.1，k 值的选取

• k 值较小，模型会变得复杂，容易发生过拟合
• k 值较大，模型比较简单，容易欠拟合

所以 k 值得选取也是一种调参？

1.2，KNN 算法思路

KNN 思想就是在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前 K 个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：

1. 计算测试数据与各个训练数据之间的距离；
2. 按照距离的递增关系进行排序；
3. 选取距离最小的 K 个点；
4. 确定前 K 个点所在类别的出现频率；
5. 返回前 K 个点中出现频率最高的类别作为测试数据的预测分类。

二，支持向量机算法

机器学习中的算法(2)-支持向量机(SVM)基础

2.1，支持向量机简述

• 支持向量机（Support Vector Machines, SVM）是一种二分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；支持向量机还包括核技巧，这使其成为实质上的非线性分类器。
• SVM 的学习策略是找到最大间隔（两个异类支持向量到超平面的距离之和 $\gamma =\frac{2}{||w}$ 称为“间隔”），可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。
• SVM 的最优化算法是求解凸二次规划的最优化算法。

2.2，SVM 基本型

$$\begin{gathered} min\frac{1}{2}||w|{|}^2 \\ s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2,...,m \end{gathered}$$

SVM 的最优化算法是一个凸二次规划（convex quadratic programming）问题，对上式使用拉格朗日乘子法可转化为对偶问题，并优化求解。

2.3，对偶问题求解

对 SVM 基本型公式的每条约束添加拉格朗日乘子 ${\alpha }_i\ge 0$，则式子的拉格朗日函数如下：

$$L(w,b,a)=\frac{1}{2}||w|{|}^2-\sum i=1n{\alpha }_i(y_i(w^T{x}_i+b)-1)$$

经过推导（参考机器学习西瓜书），可得 SVM 基本型的对偶问题：

$$\underset{\alpha }{\max }\sum _{i=1}^m-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}^T\_i{x}_j$$
$$s.t.\sum _{i=1}^m={\alpha }_i{y}_i=0$$
$${\alpha }_i\ge 0,i=1,2,...,m$$

继续优化该问题，有 SMO 方法，SMO 的基本思路是先固定 ${\alpha }_i$ 之外的的所有参数，然后求 ${\alpha }_i$ 上的极值。

三，K-means 聚类算法

3.1，分类与聚类算法

• 分类简单来说，就是根据文本的特征或属性，划分到已有的类别中。也就是说，这些类别是已知的，通过对已知分类的数据进行训练和学习，找到这些不同类的特征，再对未分类的数据进行分类。
• 聚类，就是你压根不知道数据会分为几类，通过聚类分析将数据或者说用户聚合成几个群体，那就是聚类了。聚类不需要对数据进行训练和学习。
• 分类属于监督学习，聚类属于无监督学习。常见的分类比如决策树分类算法、贝叶斯分类算法等聚类的算法最基本的有系统聚类，K-means 均值聚类。

3.2，K-means 聚类算法

聚类的目的是找到每个样本 $x$ 潜在的类别 $y$，并将同类别 $y$ 的样本 $x$ 放在一起。在聚类问题中，假定训练样本是 $x^1,...,x^m$，每个 $x^i\in R^n$，没有 $y$。K-means 算法是将样本聚类成 $k$ 个簇（cluster），算法过程如下：

1. 随机选取 $k$ 个聚类中心（cluster centroids）为 ${\mu }_1,{\mu }_1,...,{\mu }_k\in R^n$。
2. 重复下面过程，直到质心不变或者变化很小：
   • 对于每一个样例 $i$ ，计算其所属类别：$$c^i=\underset{j}{\mathrm{argmin}}||x^i-{\mu }_j|{|}^2$$
   • 对于每一个类 $j$，重新计算该类的质心：$${\mu }_j=\frac{{\sum }_{i=1}^{m}1c^i=j{x}^i}{{\sum }_{i=1}^{m}1c^i=j}$$

$K$ 是我们事先给定的聚类数，$c^i$ 代表样例 $i$ 与 $k$ 个类中距离最近的那个类，$c^i$ 的值是 $1$ 到 $k$ 中的一个。质心 ${\mu }_j$ 代表我们对属于同一个类的样本中心点的猜测。

参考资料

K-means聚类算法