中医治病——关联分析挖掘

之前一直学习各种关联分析算法，这回想实战一下。可参考《数据分析与挖掘实战》第八章

挖掘目标

借助三阴乳腺癌患者的病理信息，挖掘患者的症状与中医振型之间的关联关系

对截断治疗提供依据，挖掘潜性证素

挖掘流程

1、原始数据整理

2、数据的预处理，包括数据清洗、属性规约、数据变换

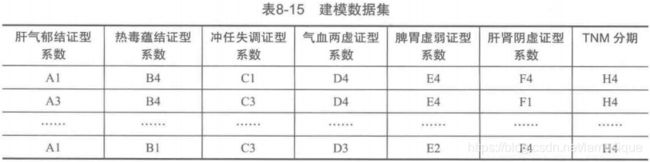
3、基于建模数据，采用关联规则算法，调整模型输入参数，获取中医证素与癌症TNM分期之间的关系

4、结合实际，模型分析，输出规则结果

1、数据采集调查

2、数据预处理

1. 数据清洗——人工删减无效的问卷

2. 属性规约——将冗余属性以及不相关的属性删除。本处保存六种属性

3. 数据变换

这步就很需要思路了。每个属性就可以代表一个特征，但是往往特征值太大就不太好，他的内部结构容易失控，所以我们都希望去做一个normaltion，把他的属性得分往-1~1之间压缩，所以我们这里可以归一化操作，具体方法就是最简单求比例。

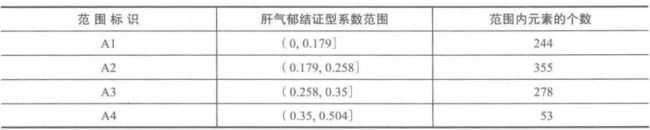
证型相关系数计算公式：振型系数=该证型得分 / 该列证型总分。最终得到下图结果

这就是我们所说的属性构造（1）。

还有今天刚提到的，为什么有些特征不好做，就是因为其特征是连续的，建模时他的非线性程度不高，就很难得到比较好的非线性表示，所以我们需要将连续特征把他离散化，对！这就是挖掘过程中往往去思考优化的问题。这一步就叫做数据特征离散化（2）。

怎么特征离散化？这又是下一步思考的问题。也就是连续个点怎么变成离散个区域？哎哟，设定区间是不是一个办法，进一步模糊判断是不是个办法，再上升到她自己寻找合适的区域。。。对了，他通过不断地探索对数据点进行自聚合，这不就是无监督学习吗？！！！很兴奋的是，我们不就可以采用K-means算法，K-means++算法等等了吗？？？！！！哈哈哈问题就被细化成这般了！

聚类分析，代码如下：

from __future__ import print_function
import pandas as pd
from sklearn.cluster import KMeans

dataFile = 'data.xls'  # 待聚类的数据文件
processedFile = 'processed_data.xls'
k = 4
keys = list([u'肝气郁结证型系数', u'热毒蕴结证型系数', u'冲任失调证型系数', u'气血两虚证型系数', u'脾胃虚弱证型系数', u'肝肾阴虚证型系数'])
labels = ['A', 'B', 'C', 'D', 'E', 'F']

# 读取数据并进行聚类分析
data = pd.read_excel(dataFile)
# print(data)
result = pd.DataFrame()
# print(result)

if __name__ == "__main__":
    for i in range(len(keys)):
        # 调用k_mean算法
        print("正在进行", keys[i], "的聚类离散化")
        x = data[[keys[i]]]
        # print(type(x))  # 
        kmodel = KMeans(n_clusters=k, n_jobs=4)
        kmodel.fit(x.values)
        # kmodel.fit(data[[keys[i]]].values)  # 训练模型
        print(kmodel.cluster_centers_)

        r1 = pd.DataFrame(kmodel.cluster_centers_, columns=[labels[i]])  # 聚类中心
        r2 = pd.Series(kmodel.labels_).value_counts()  # 分类统计
        r2 = pd.DataFrame(r2, columns=[labels[i] + 'n'])  # 转为DataFrame，记录各个类别的数目
        # print(r1,r2)
        r = pd.concat([r1, r2], axis=1).sort_values(labels[i])
        r.index = [1, 2, 3, 4] #修改index
        print(r)

        r[labels[i]]=r.rolling(2).mean()  # rolling_mean()用来计算相邻2列的均值，以此作为边界点。
        r[labels[i]][1] = 0.0  # 这两句代码将原来的聚类中心改为边界点。
        print(r.T)
        result = result.append(r.T)

    print('\n')
    result = result.sort_index(axis=1)  # 以Index列名排序，即以A,B,C,D,E,F顺序排
    print(result)
    result.to_excel(processedFile)

最终生成的表为

对这个表格整理一下，似乎我们可以进一步得到离散化后的特征A（特征B~F就不给出）

无非就是通过聚类得到各聚集簇的范围，划分为区间进行统计。

那么就对原表格进行重新统计：

采用统计代码如下：

import pandas as pd
import numpy as np

dataFile = 'data.xls'  # 待聚类的数据文件
processedFile = 'processed_data.xls'

outputFile = 'Feature.xls'
txtfile = 'feature.txt'

df = pd.read_excel(dataFile)
dfp = pd.read_excel(processedFile).T
result = pd.DataFrame()

keys = list([u'肝气郁结证型系数', u'热毒蕴结证型系数', u'冲任失调证型系数', u'气血两虚证型系数', u'脾胃虚弱证型系数', u'肝肾阴虚证型系数'])
labels = ['A', 'B', 'C', 'D', 'E', 'F']


# print(df,dfp)

def func(x, m, n):
    if x >= m and x < n:
        return 1
    else:
        return 0


for i in range(len(keys)):
    # for i in range(1):
    dfx = df[keys[i]]
    dfpx = dfp[labels[i]].iloc[:]
    # print(dfpx)
    x1 = x2 = x3 = x4 = dfx.iloc[:]

    dfx[x1 < dfpx[2]] = labels[i] + str(1)

    # dfx[x2.apply(lambda x: func(x,dfpx[2],dfpx[3]))] = labels[i] + str(2) #通过设置函数实现

    dfx[(x2 < dfpx[3]) & (x2 >= dfpx[2])] = labels[i] + str(2)
    dfx[(x3 < dfpx[4]) & (x3 >= dfpx[3])] = labels[i] + str(3)
    dfx[x4 >= dfpx[4]] = labels[i] + str(4)
    print(dfx)

    result = result.append(dfx)

result = result.append(df[u'TNM分期'])
result = result.T
result.to_excel(outputFile)


# 生成txt文件
# print(result.values)
txtVal=result.values
with open(txtfile,'w+') as f:
    for rows in txtVal:
        print(','.join(rows))
        f.write(','.join(rows))
        f.write('\n')

f.close()

pandas的操作也是费了好多时间，具体可参照：https://www.zhangshengrong.com/p/2EaE0QEO1M/

3、关联分析-模型构建

关联规则算法主要用于寻找数据集中项之间的关联关系，它揭示了数据项间的未知关系。基于样本的统计规律，进行关联规则挖掘。根据所挖掘的关联关系，可以从一个属性的信息来推断另一个属性的信息。当置信度达到某一阈值时，这就可以认为规则成立。

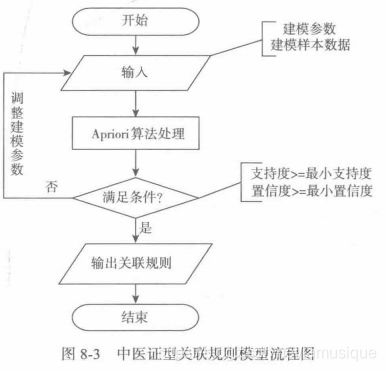
模型主要采用输入、算法处理、输出组成。输入包括：样本数据的输入，建模参数的输入；算法处理就是Apriori关联规则算法，输出为关联规则结果。

实现步骤：

另外，对于最小支持度，最小置信度的设置最优问题则根据反复测试，或者交叉验证来确定一个合适的值。此处最小支持度6%，最小置信度75%。至于关联算法 https://www.cnblogs.com/qwertWZ/p/4510857.html 自己去学习。

from __future__ import print_function
import pandas as pd
from apriori import *
import time

inputfile = "feature.txt"
# inputfile = "apriori.txt"
data = pd.read_csv(inputfile, header=None, dtype=object)
print(data.shape)

start = time.clock()  # 计时开始
print(u'\n转换原始数据至0-1矩阵...')
ct = lambda x: pd.Series(1, index=x[pd.notnull(x)])  # 转换0-1矩阵的过渡函数
b = map(ct, data.values)  # 用map方式执行
c = list(b)
data = pd.DataFrame(c).fillna(0)  # 实现矩阵转换，空值用0填充
end = time.clock()  # 计时结束
print(u'\n转换完毕，用时：%0.2f秒' % (end - start))
del b  # 删除中间变量b，节省内存

support = 0.06  # 最小支持度
confidence = 0.75  # 最小置信度
ms = '---'  # 连接符，默认'--'，用来区分不同元素，如A--B。需要保证原始表格中不含有该字符

start = time.clock()  # 计时开始
print(u'\n开始搜索关联规则...')
find_rule(data, support, confidence, ms)
end = time.clock()  # 计时结束
print(u'\n搜索完成，用时：%0.2f秒' % (end - start))

最终得到一个规则输出结果

结果分析：

我来解释一下，这是什么意思。support表示最小支持度，也即是说这个规则表示的事件占据样本的比例，比例越高说明这个规则的支持度越高；confidence表示最小置信度，也就是这个规则的信任程度值，信任值越高说明这个规则的发生的可能性越高。

我们得出了两个关联规则：
A3---F4---H4  表示A3和F4都在 可导致H4 （A3+F4===>H4）  可能性为0.880952 规则支持度0.79570
C3---F4---H4  表示C3和F4都在 可导致H4 （C3+F4===>H4）  可能性为0.875000 规则支持度0.075269    

（如出现B2---E3---H4---D2表示B2+E3+H4===>D2，说明其算法内部是无序的，他更多是看集合组成的数量(频繁项集)，而对我们判别来说该结果是无效的，因为他的输出应该是分类标签H.x）