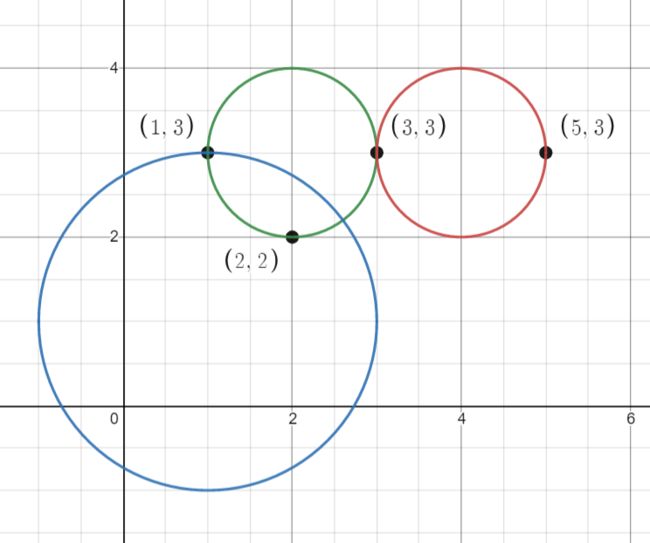【LeetCode每日一题】【2023/1/24】1828. 统计一个圆中点的数目

---

1828. 统计一个圆中点的数目

LeetCode: 1828. 统计一个圆中点的数目

$中等$

给你一个数组 points ，其中 points[i] = [x_i, y_i] ，表示第 i 个点在二维平面上的坐标。多个点可能会有 相同 的坐标。

同时给你一个数组 queries ，其中 queries[j] = [x_j, y_j, r_j] ，表示一个圆心在 (x_j, y_j) 且半径为 r_j 的圆。

对于每一个查询 queries[j] ，计算在第 j 个圆 内 点的数目。如果一个点在圆的 边界上 ，我们同样认为它在圆 内 。

请你返回一个数组 answer ，其中 answer[j] 是第 j 个查询的答案。

示例 1：

输入：points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
输出：[3,2,2]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆。

示例 2：

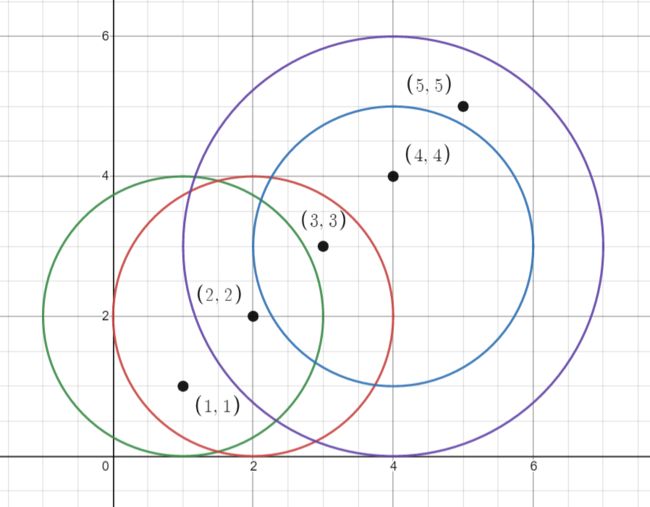
输入：points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
输出：[2,3,2,4]
解释：所有的点和圆如上图所示。
queries[0] 是绿色的圆，queries[1] 是红色的圆，queries[2] 是蓝色的圆，queries[3] 是紫色的圆。

提示：

• 1 <= points.length <= 500
• points[i].length == 2
• 0 <= x_​​​​​​i, y​​​​​​_i <= 500
• 1 <= queries.length <= 500
• queries[j].length == 3
• 0 <= x_j, y_j <= 500
• 1 <= r_j <= 500
• 所有的坐标都是整数。

---

方法1：枚举

使用一个二重循环。外层循环遍历圆及圆心，即数组 queries ；对于每一个圆，在内层循环遍历点，即数组 points 。对于每一个圆和每一个点，都判断点是否在圆内，若成立则相应圆内的点计数自增。

#include 
using namespace std;

class Solution
{
public:
    static int square(const int x)
    {
        return int(x * x);
    }

    vector<int> countPoints(const vector<vector<int>> &points, const vector<vector<int>> &queries)
    {
        vector<int> ans(queries.size(), 0);

        for (int i = 0; i < queries.size(); ++i)
        {
            const int &x = queries[i][0], &y = queries[i][1], &r = queries[i][2];
            const int r_square = square(r);
            for (const vector<int> &point : points)
            {
                if (square(point[0] - x) + square(point[1] - y) <= r_square)
                    ans[i]++;
            }
        }
        return ans;
    }
};

复杂度分析：

• 时间复杂度：$O(n\times m)$。其中，$n$ 为数组 queries 的长度，$m$ 为数组 points 的长度。

• 空间复杂度：$O(1)$。没有用到额外的、大小与输入数据有关的变量，因此仅占用常数的额外空间。

参考结果

Accepted
66/66 cases passed (60 ms)
Your runtime beats 93.60 % of cpp submissions
Your memory usage beats 68.80 % of cpp submissions (15.8 MB)