机器学习笔记之生成模型综述(二)监督学习与无监督学习
机器学习笔记之生成模型综述——监督学习与无监督学习
- 引言
-
- 回顾:生成模型介绍
-
- 判别方式:生成模型 VS \text{VS} VS 判别模型
- 生成模型的建模手段
- 监督学习与无监督学习
-
- 监督学习模型
-
- 基于监督学习的非概率模型
- 基于监督学习的概率模型
- 无监督学习
-
- 基于无监督学习的概率模型
- 基于无监督学习的非概率模型
- 生成模型介绍
引言
上一节介绍了生成模型的判别方式,本节将从机器学习需要解决的任务——监督学习、无监督学习的角度,对现阶段经典模型进行总结。
回顾:生成模型介绍
判别方式:生成模型 VS \text{VS} VS 判别模型
生成模型( Generative Model \text{Generative Model} Generative Model)的核心判别方式是:建模所关注的对象是否在样本分布自身。例如逻辑回归与朴素贝叶斯分类器。虽然这两个算法均处理基于监督学习的分类任务,并且均是软分类算法,但关注点截然不同:
-
逻辑回归( Logistic Regression \text{Logistic Regression} Logistic Regression)的底层逻辑是最大熵原理,通过 Sigmoid , Softmax \text{Sigmoid},\text{Softmax} Sigmoid,Softmax函数直接对后验概率 P ( Y ∣ X ) \mathcal P(\mathcal Y \mid \mathcal X) P(Y∣X)进行描述:
以二分类为例,此时Y \mathcal Y Y服从伯努利分布。
P ( Y ∣ X ) = { Sigmoid ( W T X + b ) Y = 1 1 − Sigmoid ( W T X + b ) Y = 0 \mathcal P(\mathcal Y \mid \mathcal X) = \begin{cases} \text{Sigmoid}(\mathcal W^T\mathcal X + b) \quad \mathcal Y = 1\\ 1 - \text{Sigmoid}(\mathcal W^T\mathcal X + b) \quad \mathcal Y = 0 \end{cases} P(Y∣X)={Sigmoid(WTX+b)Y=11−Sigmoid(WTX+b)Y=0
很明显,这里我们仅关注 Sigmoid \text{Sigmoid} Sigmoid函数结果。而 X \mathcal X X的特征信息仅作为与模型参数 W \mathcal W W做内积的工具而已,并不是我们关注的对象; -
朴素贝叶斯分类器( Naive Bayes Classifier \text{Naive Bayes Classifier} Naive Bayes Classifier)针对后验概率 P ( Y ∣ X ) \mathcal P(\mathcal Y \mid \mathcal X) P(Y∣X),通过贝叶斯定理将其转化为 P ( X ∣ Y ) ⋅ P ( Y ) \mathcal P(\mathcal X \mid \mathcal Y) \cdot \mathcal P(\mathcal Y) P(X∣Y)⋅P(Y)之间的大小关系:
关于分母P ( X ) \mathcal P(\mathcal X) P(X)的完整形式是∫ Y P ( X ∣ Y ) ⋅ P ( Y ) d Y \int_{\mathcal Y}\mathcal P(\mathcal X \mid \mathcal Y) \cdot \mathcal P(\mathcal Y) d\mathcal Y ∫YP(X∣Y)⋅P(Y)dY,该项自身与Y \mathcal Y Y无关,可视作常数。这里依然以二分类为例,Y \mathcal Y Y同样服从伯努利分布。
P ( Y ∣ X ) = P ( X , Y ) P ( X ) ∝ P ( X , Y ) = P ( X ∣ Y ) ⋅ P ( Y ) P ( X ∣ Y = 0 ) ⋅ P ( Y = 0 ) ⇔ ? P ( X ∣ Y = 1 ) ⋅ P ( Y = 1 ) \begin{aligned} \mathcal P(\mathcal Y \mid \mathcal X) = \frac{\mathcal P(\mathcal X,\mathcal Y)}{\mathcal P(\mathcal X)} \propto \mathcal P(\mathcal X,\mathcal Y) = \mathcal P(\mathcal X \mid \mathcal Y) \cdot \mathcal P(\mathcal Y) \\ \mathcal P(\mathcal X \mid \mathcal Y = 0) \cdot \mathcal P(\mathcal Y = 0) \overset{\text{?}}{\Leftrightarrow} \mathcal P(\mathcal X \mid \mathcal Y = 1) \cdot \mathcal P(\mathcal Y = 1) \end{aligned} P(Y∣X)=P(X)P(X,Y)∝P(X,Y)=P(X∣Y)⋅P(Y)P(X∣Y=0)⋅P(Y=0)⇔?P(X∣Y=1)⋅P(Y=1)
在这里,我们关注的对象是联合概率分布 P ( X , Y ) \mathcal P(\mathcal X,\mathcal Y) P(X,Y)。并且针对 P ( X , Y ) \mathcal P(\mathcal X,\mathcal Y) P(X,Y)建模的过程中,设计了朴素贝叶斯假设:
{ x i ⊥ x j ∣ Y ( i ≠ j ; x i , x j ∈ X ; X ∈ R p ) P ( X ∣ Y ) = P ( x 1 , ⋯ , x p ∣ Y ) = ∏ i = 1 p P ( x i ∣ Y ) \begin{cases} x_i \perp x_j \mid \mathcal Y \quad (i\neq j;x_i,x_j \in \mathcal X;\mathcal X \in \mathbb R^p) \\ \mathcal P(\mathcal X \mid \mathcal Y) = \mathcal P(x_1,\cdots,x_p \mid \mathcal Y) = \prod_{i=1}^p \mathcal P(x_i \mid \mathcal Y) \end{cases} {xi⊥xj∣Y(i=j;xi,xj∈X;X∈Rp)P(X∣Y)=P(x1,⋯,xp∣Y)=∏i=1pP(xi∣Y)
生成模型的建模手段
如果针对监督学习,自带标签信息 Y \mathcal Y Y,例如朴素贝叶斯分类器,通常针对联合概率分布 P ( X , Y ) \mathcal P(\mathcal X,\mathcal Y) P(X,Y)进行建模;
如果是无监督学习,此时只有样本特征 X \mathcal X X,主要分为两种情况:
- 如自回归模型( Autoregressive Model,AR \text{Autoregressive Model,AR} Autoregressive Model,AR),它直接对 P ( X ) \mathcal P(\mathcal X) P(X)自身进行建模;
- 隐变量模型( Latent Variable Model,LVM \text{Latent Variable Model,LVM} Latent Variable Model,LVM),通过假设隐变量 Z \mathcal Z Z,对联合概率分布 P ( X , Z ) \mathcal P(\mathcal X,\mathcal Z) P(X,Z)进行建模。
监督学习与无监督学习
从机器学习任务的角度观察:
- 分类( Classification \text{Classification} Classification)、回归( Regression \text{Regression} Regression) 等明显属于监督学习任务;
- 而像降维( Dimensionality Reduction \text{Dimensionality Reduction} Dimensionality Reduction)、聚类( Cluster \text{Cluster} Cluster)、数据生成( Data Generation \text{Data Generation} Data Generation) 等属于无监督学习任务。
无论是监督学习还是无监督学习,都可以将其划分为概率模型与非概率模型。
这里的概率模型/非概率模型是指:在建模的过程中,其关于任务的返回结果是否考虑了概率分布。换句话说,概率是否直接参与到相关任务中去。
监督学习模型
基于监督学习的非概率模型
监督学习中的非概率模型,大方向指的是判别模型。在分类任务中,硬分类模型都是非概率模型。
- 感知机算法( Perceptron Linear Alpgorithm,PLA \text{Perceptron Linear Alpgorithm,PLA} Perceptron Linear Alpgorithm,PLA) :硬分类任务的对应模型均表示特征空间的超平面。区别在于样本划分的策略(模型表示后略):
其中Sign \text{Sign} Sign函数表示指示函数,在硬分类任务中,其大多指的是分段函数;而在软分类任务中,它可以是如Sigmoid \text{Sigmoid} Sigmoid函数的连续函数。
Y = Sign ( W T X + b ) \mathcal Y = \text{Sign}(\mathcal W^T\mathcal X + b) Y=Sign(WTX+b)
感知机算法的策略是错误驱动:
{ L ( W , b ) = ∑ ( x ( i ) , y ( i ) ∈ D ) − y ( i ) ( W T x ( i ) + b ) arg min W , b L ( W , b ) \begin{cases} \mathcal L(\mathcal W,b) = \sum_{(x^{(i)},y^{(i)} \in \mathcal D)} -y^{(i)}\left(\mathcal W^Tx^{(i)} + b \right) \\ \mathop{\arg\min}\limits_{\mathcal W,b} \mathcal L(\mathcal W,b) \end{cases} ⎩ ⎨ ⎧L(W,b)=∑(x(i),y(i)∈D)−y(i)(WTx(i)+b)W,bargminL(W,b) - 硬间隔-支持向量机( Support Vector Machine,SVM \text{Support Vector Machine,SVM} Support Vector Machine,SVM),区别其他的硬分类模型,它是一个带约束的优化问题:
{ min W , b 1 2 W T W s . t . y ( i ) ( W T x ( i ) + b ) ≥ 1 ( x ( i ) , y ( i ) ) ∈ D \begin{cases} \mathop{\min}\limits_{\mathcal W,b} \frac{1}{2}\mathcal W^T\mathcal W \\ s.t. y^{(i)} \left(\mathcal W^Tx^{(i)} + b\right) \geq 1 \quad (x^{(i)},y^{(i)}) \in \mathcal D \end{cases} ⎩ ⎨ ⎧W,bmin21WTWs.t.y(i)(WTx(i)+b)≥1(x(i),y(i))∈D - 线性判别分析( Linear Discriminant Analysis,LDA \text{Linear Discriminant Analysis,LDA} Linear Discriminant Analysis,LDA):以二分类为例,通过描述被超平面划分样本点的类内、类间关系,来确定模型参数信息。其策略表示如下:
J ( W ) = ( Z 1 ˉ − Z 2 ) 2 ˉ S 1 + S 2 = W T ( X C 1 ˉ − X C 2 ˉ ) ( X C 1 ˉ − X C 2 ˉ ) T W W T ( S C 1 + S C 2 ) W { S C 1 = 1 N 1 ∑ i = 1 N 1 ( x ( i ) − X C 1 ˉ ) ( x ( i ) − X C 1 ˉ ) T X C 1 ˉ = 1 N 1 ∑ i = 1 N 1 x ( i ) \begin{aligned} \mathcal J(\mathcal W) & = \frac{(\bar{\mathcal Z_1} - \bar{\mathcal Z_2)^2}}{\mathcal S_1 + \mathcal S_2} \\ & = \frac{\mathcal W^T(\bar{\mathcal X_{\mathcal C_1}} - \bar{\mathcal X_{\mathcal C_2}})(\bar{\mathcal X_{\mathcal C_1}} - \bar{\mathcal X_{\mathcal C_2}})^T \mathcal W}{\mathcal W^T(\mathcal S_{\mathcal C_1} + \mathcal S_{\mathcal C_2}) \mathcal W} \\ & \begin{cases} \mathcal S_{\mathcal C_1} = \frac{1}{N_1} \sum_{i=1}^{N_1} (x^{(i)} - \bar{\mathcal X_{\mathcal C_1}})(x^{(i)} - \bar{\mathcal X_{\mathcal C_1}})^T \\ \bar {\mathcal X_{\mathcal C_1}} = \frac{1}{N_1} \sum_{i=1}^{N_1} x^{(i)} \end{cases} \end{aligned} J(W)=S1+S2(Z1ˉ−Z2)2ˉ=WT(SC1+SC2)WWT(XC1ˉ−XC2ˉ)(XC1ˉ−XC2ˉ)TW{SC1=N11∑i=1N1(x(i)−XC1ˉ)(x(i)−XC1ˉ)TXC1ˉ=N11∑i=1N1x(i) - 多层感知机/前馈神经网络( Feed-Forword Neural Network \text{Feed-Forword Neural Network} Feed-Forword Neural Network):其核心是通用逼近定理。
- 关于神经网络处理硬分类问题,例如亦或问题,可以将其视作非概率判别模型;
基于亦或问题的前馈神经网络结构表示如下。

- 如果是软分类问题,如在网络输出层加上 Sigmoid,Softmax \text{Sigmoid,Softmax} Sigmoid,Softmax函数作为输出,它此时被视作概率判别模型。
Sigmoid,Softmax \text{Sigmoid,Softmax} Sigmoid,Softmax函数将输出结果映射成了概率分布形式,并且是以X \mathcal X X作为输入层,关于Y \mathcal Y Y的后验概率P ( Y ∣ X ) \mathcal P(\mathcal Y \mid \mathcal X) P(Y∣X). - 如果是回归任务,并不称其为判别模型,能够确定的是,它是一个非概率模型。
- 关于神经网络处理硬分类问题,例如亦或问题,可以将其视作非概率判别模型;
- 除了基于直线/超平面形状的硬分类算法,还如其他算法如决策树( Decision Tree \text{Decision Tree} Decision Tree)等其他树模型也属于监督学习中的非概率模型。
基于监督学习的概率模型
监督学习中的概率模型可以继续向下划分,可划分为概率判别模型( Discriminative Model \text{Discriminative Model} Discriminative Model)和概率生成模型( Generative Model \text{Generative Model} Generative Model)两种:
‘概率生成模型’在末尾统一介绍。
-
其中概率判别模型的核心思想是:直接对条件概率 P ( Y ∣ X ) \mathcal P(\mathcal Y \mid \mathcal X) P(Y∣X)进行建模 。经典的概率判别模型有:
- 逻辑回归( Logistic Regression,LR \text{Logistic Regression,LR} Logistic Regression,LR):它的模型结构与其他分类任务的非概率模型相同,均是特征空间的直线/超平面:
这里的Sign \text{Sign} Sign函数指的是Sigmoid \text{Sigmoid} Sigmoid函数自身。
Y = Sigmoid ( W T X + b ) \mathcal Y = \text{Sigmoid}(\mathcal W^T\mathcal X + b) Y=Sigmoid(WTX+b)
假设标签信息 Y \mathcal Y Y服从伯努利分布,逻辑回归使用 Sigmoid \text{Sigmoid} Sigmoid函数直接对 P ( Y ∣ X ) \mathcal P(\mathcal Y \mid \mathcal X) P(Y∣X)进行表达:
其中W , b \mathcal W,b W,b分别表示权重参数与偏置信息。
P ( Y ∣ X ) = { Sigmoid ( W T X + b ) Y = 1 1 − Sigmoid ( W T X + b ) Y = 0 \mathcal P(\mathcal Y \mid \mathcal X) = \begin{cases} \text{Sigmoid}(\mathcal W^T\mathcal X + b) \quad \mathcal Y = 1 \\ 1 - \text{Sigmoid}(\mathcal W^T\mathcal X + b) \quad \mathcal Y = 0 \end{cases} P(Y∣X)={Sigmoid(WTX+b)Y=11−Sigmoid(WTX+b)Y=0 - 最大熵马尔可夫模型( Maximum Entropy Markov Model,MEMM \text{Maximum Entropy Markov Model,MEMM} Maximum Entropy Markov Model,MEMM):该模型的概率图结构表示如下:
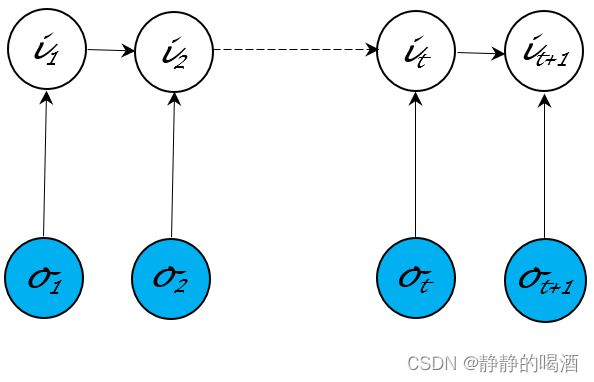
这种概率图结构打破了观测独立性假设的约束。并且它直接对隐变量 I \mathcal I I的后验概率进行建模:
P ( I ∣ O ; λ ) = P ( i 1 , ⋯ , i T ∣ o 1 , ⋯ , o T ; λ ) = P ( i 1 ∣ o 1 ; λ ) ⋅ ∏ t = 2 T P ( i t ∣ i t − 1 , o t ; λ ) \begin{aligned} \mathcal P(\mathcal I \mid \mathcal O;\lambda) & = \mathcal P(i_1,\cdots,i_{T} \mid o_1,\cdots,o_{T};\lambda) \\ & = \mathcal P(i_1 \mid o_1;\lambda) \cdot \prod_{t=2}^{T} \mathcal P(i_t \mid i_{t-1},o_t;\lambda) \end{aligned} P(I∣O;λ)=P(i1,⋯,iT∣o1,⋯,oT;λ)=P(i1∣o1;λ)⋅t=2∏TP(it∣it−1,ot;λ) - 条件随机场( Condition Random Field,CRF \text{Condition Random Field,CRF} Condition Random Field,CRF) :该模型的概率图结构表示如下:
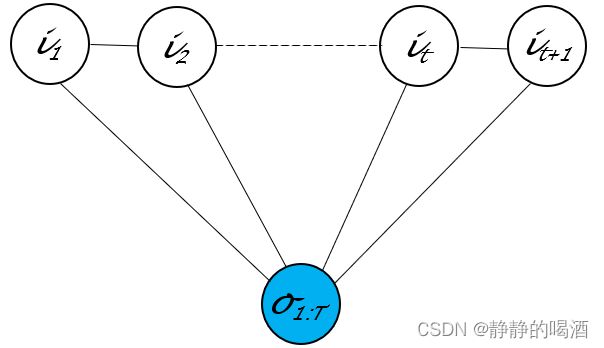
在给定观测变量 O \mathcal O O的条件下,直接对 P ( I ∣ O ) \mathcal P(\mathcal I \mid \mathcal O) P(I∣O)进行建模:
关于这种链式的无向图结构,它的极大团内仅包含相邻的两个随机变量结点与观测变量结点,这里将极大团数量K \mathcal K K替换为序列长度T T T;并且− E k ( i C k ) -\mathbb E_{k}(i_{\mathcal C_k}) −Ek(iCk)表示能量函数,恒正;Z \mathcal Z Z表示配分函数。
P ( I ∣ O ) = 1 Z exp ∑ k = 1 K − E k ( i C k ) = 1 Z exp ∑ t = 1 T f t ( i t , i t + 1 , O ⏟ 极大团 t 内部结点 ) \begin{aligned} \mathcal P(\mathcal I \mid \mathcal O) & = \frac{1}{\mathcal Z} \exp \sum_{k=1}^{\mathcal K} - \mathbb E_{k}(i_{\mathcal C_k}) \\ & = \frac{1}{\mathcal Z} \exp \sum_{t=1}^{T} f_t(\underbrace{i_t,i_{t+1},\mathcal O}_{极大团t内部结点}) \end{aligned} P(I∣O)=Z1expk=1∑K−Ek(iCk)=Z1expt=1∑Tft(极大团t内部结点 it,it+1,O)
从上述介绍的几种模型也能观察到:并不能将所有的隐变量模型武断地看作生成模型,对于判别模型与生成模型的界限存在新的认识。
- 逻辑回归( Logistic Regression,LR \text{Logistic Regression,LR} Logistic Regression,LR):它的模型结构与其他分类任务的非概率模型相同,均是特征空间的直线/超平面:
无监督学习
基于无监督学习的概率模型
由于无监督学习中没有标签信息,仅包含样本特征,因此无法通过标签信息进行判别。因而基于无监督的概率模型只有概率生成模型。
这里所说的概率分布只会是样本 X \mathcal X X的概率分布,在下面统一介绍。
基于无监督学习的非概率模型
关于无监督学习的非概率模型主要针对于特定任务。如:
- 降维-主成分分析( Principal Component Analysis,PCA \text{Principal Component Analysis,PCA} Principal Component Analysis,PCA):在执行去中心化操作后,找到主成分 u ⃗ \vec u u,使 u ⃗ \vec u u满足如下条件:
{ u ^ = arg max u ⃗ J { J = u ⃗ T ⋅ [ 1 N ∑ i = 1 N ( x ( i ) − X ˉ ) ( x ( i ) − X ˉ ) T ] ⋅ u ⃗ X ˉ = 1 N ∑ i = 1 N x ( i ) s . t . u ⃗ T ⋅ u ⃗ = 1 \begin{cases} \hat u = \mathop{\arg\max}\limits_{\vec u} \mathcal J \quad \begin{cases} \mathcal J = \vec u^T \cdot \left[\frac{1}{N} \sum_{i=1}^N(x^{(i)} - \bar {\mathcal X})(x^{(i)} - \bar {\mathcal X})^T \right] \cdot \vec u \\ \bar {\mathcal X} = \frac{1}{N} \sum_{i=1}^N x^{(i)} \end{cases}\\ s.t. \quad \vec u^T \cdot \vec u = 1 \\ \end{cases} ⎩ ⎨ ⎧u^=uargmaxJ{J=uT⋅[N1∑i=1N(x(i)−Xˉ)(x(i)−Xˉ)T]⋅uXˉ=N1∑i=1Nx(i)s.t.uT⋅u=1 - 其他的非概率模型如用于聚类任务的 K-means \text{K-means} K-means,以及自编码器( Autoencoder \text{Autoencoder} Autoencoder)等等。
生成模型介绍
关于生成模型,将其从监督任务、非监督任务进行划分,意义不大。因而统一进行描述。首先需要排除一些错误认知:
- 概率图模型,特别是隐变量模型,并不全是生成模型。
如上面介绍的最大熵马尔可夫模型、条件随机场,它们是判别模型。只能说概率图模型中的大部分模型是生成模型。 - 相反,生成模型也并不全是概率图模型,例如神经网络。
- 在处理回归任务中,前馈神经网络结构可以视作非概率模型。如线性回归( Linear Regression \text{Linear Regression} Linear Regression);
- 在处理硬分类任务中,如前馈神经网络处理亦或问题,此时的前馈神经网络结构可以视作非概率的判别模型;
- 在处理软分类任务,如逻辑回归,此时的前馈神经网络结构可以视作概率判别模型;
- 在无监督学习任务中,针对非概率模型有自编码器( Auto-Encoder \text{Auto-Encoder} Auto-Encoder);
- 基于神经网络的分布式表示思想,通过神经网络实现特征提取,此时的神经网络可以被划分至概率生成模型。
也就是说,生成模型横跨了概率图模型以及深度学习,特别是将神经网络与概率图模型混合的产物——深度生成模型( Deep Generative Model \text{Deep Generative Model} Deep Generative Model)
-
在介绍的生成模型中,假设最简单的生成模型——朴素贝叶斯分类器( Naive Bayes Classifier \text{Naive Bayes Classifier} Naive Bayes Classifier),它的核心是朴素贝叶斯假设:
x i ⊥ x j ∣ Y = l { i , j ∈ { 1 , 2 , ⋯ , p } / X ∈ R p i ≠ j l ∈ { 1 , 2 , ⋯ , k } x_i \perp x_j \mid \mathcal Y = l \quad \begin{cases} i,j \in \{1,2,\cdots,p\} / \mathcal X \in \mathbb R^p \\ i \neq j \\ l \in \{1,2,\cdots,k\} \end{cases} xi⊥xj∣Y=l⎩ ⎨ ⎧i,j∈{1,2,⋯,p}/X∈Rpi=jl∈{1,2,⋯,k}
主要应用在监督学习的分类任务,对应的概率图结构表示如下:
很明显,它并不是混合模型。x 1 , ⋯ , x p x_1,\cdots,x_p x1,⋯,xp是随机变量,表示样本自身的各维度特征;Y \mathcal Y Y表示样本对应的标签信息。

-
混合模型系列,仅通过样本自身特征信息无法准确描述概率分布,需要引入隐变量 Z \mathcal Z Z进行建模。如高斯混合模型( Gaussian Mixture Model,GMM \text{Gaussian Mixture Model,GMM} Gaussian Mixture Model,GMM),其中 Z \mathcal Z Z被假设为一维、离散型随机变量,并且 X ∣ Z \mathcal X \mid \mathcal Z X∣Z服从高斯分布:
根据实际情况,也可以将其设置为其他分布,构建不同的混合模型。
X ∣ Z ∼ N ( μ k , Σ k ) \mathcal X \mid \mathcal Z \sim \mathcal N(\mu_{k},\Sigma_{k}) X∣Z∼N(μk,Σk)
对应的建模过程表示为:
关于包含隐变量生成模型的建模过程主要是对联合概率分布P ( X , Z ) \mathcal P(\mathcal X,\mathcal Z) P(X,Z)进行建模。
P ( X ) = ∑ Z P ( X , Z ) = ∑ Z P ( X ∣ Z ) ⋅ P ( Z ) = ∑ k = 1 K p k ⋅ N ( μ k , Σ k ) ( ∑ k = 1 K p k = 1 ) \begin{aligned} \mathcal P(\mathcal X) & = \sum_{\mathcal Z} \mathcal P(\mathcal X,\mathcal Z) \\ & = \sum_{\mathcal Z} \mathcal P(\mathcal X \mid \mathcal Z) \cdot \mathcal P(\mathcal Z) \\ & = \sum_{k=1}^{\mathcal K} p_{k} \cdot \mathcal N(\mu_{k},\Sigma_{k}) \quad (\sum_{k=1}^{\mathcal K} p_k = 1) \end{aligned} P(X)=Z∑P(X,Z)=Z∑P(X∣Z)⋅P(Z)=k=1∑Kpk⋅N(μk,Σk)(k=1∑Kpk=1)
主要应用在无监督学习的聚类任务。其概率图结构表示如下:

-
动态模型( Dynamic Model \text{Dynamic Model} Dynamic Model)系列:从时间、序列角度随机变量从有限到无限。代表模型有隐马尔可夫模型( Hidden Markov Model,HMM \text{Hidden Markov Model,HMM} Hidden Markov Model,HMM),卡尔曼滤波( Kalman Filter \text{Kalman Filter} Kalman Filter),粒子滤波( Praticle Filter \text{Praticle Filter} Praticle Filter)。它们均服从齐次马尔可夫假设与观测独立性假设:
{ P ( i t + 1 ∣ i t , ⋯ ) = P ( i t + 1 ∣ i t ) P ( o t ∣ i t , ⋯ ) = P ( o t ∣ i t ) \begin{cases} \mathcal P(i_{t+1} \mid i_t,\cdots) = \mathcal P(i_{t+1} \mid i_t) \\ \mathcal P(o_t \mid i_t,\cdots) = \mathcal P(o_t \mid i_t) \end{cases} {P(it+1∣it,⋯)=P(it+1∣it)P(ot∣it,⋯)=P(ot∣it)
对应的概率图结构表示如下:

-
从空间角度的随机变量从有限到无限,代表模型有高斯过程( Gaussian Process \text{Gaussian Process} Gaussian Process),准确的说,高斯过程是联合正态分布的无限维的广义延伸,主要应用在高维的非线性回归任务中:
由于连续域中的片段是无法划分完的,因此仅示例N N N个重要片段。
后续补充:狄利克雷过程~
{ ξ t } t ∈ T = { ξ t 1 , ξ t 2 , ⋯ , ξ t N } ⏟ N 个重要片段 { ξ t 1 ∼ N ( μ t 1 , Σ t 1 ) ξ t 2 ∼ N ( μ t 2 , Σ t 2 ) ⋯ ξ t N ∼ N ( μ t N , Σ t N ) \left\{\xi_t\right\}_{t \in \mathcal T} = \underbrace{\{\xi_{t_1},\xi_{t_2},\cdots,\xi_{t_{N}}\}}_{N个重要片段} \quad \begin{cases} \xi_{t_1} \sim \mathcal N(\mu_{t_1},\Sigma_{t_1}) \\ \xi_{t_2} \sim \mathcal N(\mu_{t_2},\Sigma_{t_2}) \\ \cdots \\ \xi_{t_N} \sim \mathcal N(\mu_{t_N},\Sigma_{t_N}) \\ \end{cases} {ξt}t∈T=N个重要片段 {ξt1,ξt2,⋯,ξtN}⎩ ⎨ ⎧ξt1∼N(μt1,Σt1)ξt2∼N(μt2,Σt2)⋯ξtN∼N(μtN,ΣtN)- 对比于高斯分布,仅需要知道该分布的参数(均值、方差),就可以确定一个高斯分布;
- 高斯过程中,连续域中的任意一个片段均服从一个高斯分布,它的参数可能是无限个。如高斯过程这种参数空间从有限到无限的模型,被称作 非参数贝叶斯模型( Non-Parameter Bayessian Model \text{Non-Parameter Bayessian Model} Non-Parameter Bayessian Model)。
-
以隐狄利克雷分配( Latent Dirichlet Allocation,LDA \text{Latent Dirichlet Allocation,LDA} Latent Dirichlet Allocation,LDA)为代表的 Mixed Memership Model \text{Mixed Memership Model} Mixed Memership Model。
-
以因子分析( Factorial Analysis,FA \text{Factorial Analysis,FA} Factorial Analysis,FA)为代表的因子模型( Factorial Model \text{Factorial Model} Factorial Model),其他模型有概率性主成分分析( Probabilistic Principal Component Analysis,P-PCA \text{Probabilistic Principal Component Analysis,P-PCA} Probabilistic Principal Component Analysis,P-PCA)等。
后续模型就是概率图模型与深度学习相结合的概率生成模型——深度生成模型。
- 以玻尔兹曼机( Boltzmann Machine,BM \text{Boltzmann Machine,BM} Boltzmann Machine,BM)为代表的能量模型( Energy-based Model \text{Energy-based Model} Energy-based Model)。玻尔兹曼机的概率图结构表示如下:

对应的模型表示为(对联合概率分布 P ( v , h ) \mathcal P(v,h) P(v,h)进行建模。下同):
其中v T R ⋅ v ; h T S ⋅ h ; v T W ⋅ h v^T \mathcal R \cdot v;h^T\mathcal S \cdot h;v^T\mathcal W \cdot h vTR⋅v;hTS⋅h;vTW⋅h分别表示包含边相关联结点之间的能量表达;b T v ; c T h b^Tv;c^Th bTv;cTh分别表示各结点内部的能量表达(b , c b,c b,c可看作偏置信息)
P ( v , h ) = 1 Z exp { − E [ v , h ] } = 1 Z exp { [ v T R ⋅ v + b T v + v T W ⋅ h + h T S ⋅ h + c T h ] } \begin{aligned} \mathcal P(v,h) & = \frac{1}{\mathcal Z} \exp \{- \mathbb E [v,h]\} \\ & = \frac{1}{\mathcal Z} \exp \{\left[v^T \mathcal R \cdot v + b^T v + v^T \mathcal W \cdot h + h^T\mathcal S \cdot h + c^Th\right]\} \end{aligned} P(v,h)=Z1exp{−E[v,h]}=Z1exp{[vTR⋅v+bTv+vTW⋅h+hTS⋅h+cTh]}
其中包括受限玻尔兹曼机( Restricted Boltzmann Machine,RBM \text{Restricted Boltzmann Machine,RBM} Restricted Boltzmann Machine,RBM),对应概率图结构表示如下:

对应模型表示为:
和玻尔兹曼机相比,受限玻尔兹曼机隐变量、观测变量内部各随机变量相互独立。
P ( v , h ) = 1 Z exp { − E ( v , h ) } = 1 Z exp ( v T W ⋅ h + b T v + c T h ) \begin{aligned} \mathcal P(v,h) & = \frac{1}{\mathcal Z} \exp \{-\mathbb E(v,h)\} \\ & = \frac{1}{\mathcal Z} \exp (v^T\mathcal W \cdot h + b^Tv + c^Th) \end{aligned} P(v,h)=Z1exp{−E(v,h)}=Z1exp(vTW⋅h+bTv+cTh)
Sigmoid \text{Sigmoid} Sigmoid信念网络( Sigmoid Belief Network \text{Sigmoid Belief Network} Sigmoid Belief Network),它的概率图结构表示如下:
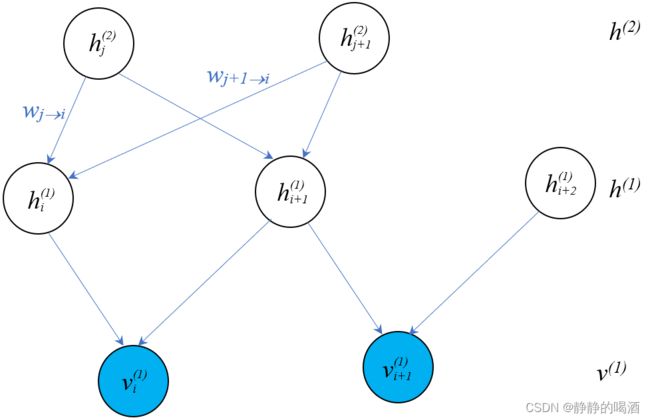
对应模型表示为:
由于Sigmoid \text{Sigmoid} Sigmoid信念网络是有向图模型,因而可以通过结点之间的因果关系对模型进行表示。
P ( v , h ) = P ( v i ( 1 ) , v i + 1 ( 1 ) , h i ( 1 ) , h i + 1 ( 1 ) , h i + 2 ( 1 ) , h j ( 2 ) , h j + 1 ( 2 ) ) = P ( h j ( 2 ) ) ⋅ P ( h j + 1 ( 2 ) ) ⋅ P ( h i ( 1 ) ∣ h j ( 2 ) , h j + 1 ( 2 ) ) ⋅ P ( h i + 1 ( 1 ) ∣ h j ( 2 ) , h j + 1 ( 2 ) ) ⋅ P ( v i ( 1 ) ∣ h i ( 1 ) , h i + 1 ( 1 ) ) ⋅ P ( h i + 2 ( 1 ) ) ⋅ P ( v i + 1 ( 1 ) ∣ h i + 1 ( 1 ) , h i + 2 ( 1 ) ) \begin{aligned} \mathcal P(v,h) & = \mathcal P (v_i^{(1)},v_{i+1}^{(1)},h_{i}^{(1)},h_{i+1}^{(1)},h_{i+2}^{(1)},h_{j}^{(2)},h_{j+1}^{(2)}) \\ & = \mathcal P(h_j^{(2)}) \cdot \mathcal P(h_{j+1}^{(2)}) \cdot \mathcal P(h_{i}^{(1)} \mid h_{j}^{(2)},h_{j+1}^{(2)}) \cdot \mathcal P(h_{i+1}^{(1)} \mid h_{j}^{(2)},h_{j+1}^{(2)}) \cdot \mathcal P(v_i^{(1)} \mid h_{i}^{(1)},h_{i+1}^{(1)}) \cdot \mathcal P(h_{i+2}^{(1)}) \cdot \mathcal P(v_{i+1}^{(1)} \mid h_{i+1}^{(1)},h_{i+2}^{(1)}) \end{aligned} P(v,h)=P(vi(1),vi+1(1),hi(1),hi+1(1),hi+2(1),hj(2),hj+1(2))=P(hj(2))⋅P(hj+1(2))⋅P(hi(1)∣hj(2),hj+1(2))⋅P(hi+1(1)∣hj(2),hj+1(2))⋅P(vi(1)∣hi(1),hi+1(1))⋅P(hi+2(1))⋅P(vi+1(1)∣hi+1(1),hi+2(1))
深度信念网络( Deep Belief Network,DBN \text{Deep Belief Network,DBN} Deep Belief Network,DBN),它的概率图结构表示如下:

对应模型表示为:
P ( v ( 1 ) , h ( 1 ) , h ( 2 ) , h ( 3 ) ) = ∏ i = 1 D P ( v i ( 1 ) ∣ h ( 1 ) ) ⋅ ∏ j = 1 P ( 1 ) P ( h j ( 1 ) ∣ h ( 2 ) ) ⋅ P ( h ( 2 ) , h ( 3 ) ) { P ( v i ( 1 ) ∣ h ( 1 ) ) = Sigmoid { [ W h ( 1 ) → v i ( 1 ) ] T h ( 1 ) + b i ( 0 ) } [ W h ( 1 ) → v i ( 1 ) ] P ( 1 ) × 1 ∈ W ( 1 ) P ( h j ( 1 ) ∣ h ( 2 ) ) = Sigmoid { [ W h ( 2 ) → h j ( 1 ) ] T h ( 2 ) + b j ( 1 ) } [ W h ( 2 ) → h j ( 1 ) ] P ( 2 ) × 1 ∈ W ( 2 ) P ( h ( 2 ) , h ( 3 ) ) = 1 Z exp { [ h ( 3 ) ] T W ( 3 ) ⋅ h ( 2 ) + [ h ( 2 ) ] T ⋅ b ( 2 ) + [ h ( 3 ) ] T b ( 3 ) } \begin{aligned} & \mathcal P(v^{(1)},h^{(1)},h^{(2)},h^{(3)}) = \prod_{i=1}^{\mathcal D} \mathcal P(v_i^{(1)} \mid h^{(1)}) \cdot \prod_{j=1}^{\mathcal P^{(1)}} \mathcal P(h_j^{(1)} \mid h^{(2)}) \cdot \mathcal P(h^{(2)},h^{(3)}) \\ & \begin{cases} \mathcal P(v_i^{(1)} \mid h^{(1)}) = \text{Sigmoid} \left\{\left[\mathcal W_{h^{(1)} \to v_i^{(1)}}\right]^T h^{(1)} + b_i^{(0)}\right\} \quad \left[\mathcal W_{h^{(1)} \to v_i^{(1)}}\right]_{\mathcal P^{(1)} \times 1} \in \mathcal W^{(1)} \\ \mathcal P(h_j^{(1)} \mid h^{(2)}) = \text{Sigmoid} \left\{\left[\mathcal W_{h^{(2)} \to h_j^{(1)}}\right]^T h^{(2)} + b_j^{(1)}\right\} \quad \left[\mathcal W_{h^{(2)} \to h_j^{(1)}}\right]_{\mathcal P^{(2)} \times 1} \in \mathcal W^{(2)} \\ \mathcal P(h^{(2)},h^{(3)}) = \frac{1}{\mathcal Z} \exp \left\{ \left[h^{(3)}\right]^T \mathcal W^{(3)} \cdot h^{(2)} + \left[h^{(2)}\right]^T\cdot b^{(2)} + \left[h^{(3)}\right]^Tb^{(3)}\right\} \\ \end{cases} \end{aligned} P(v(1),h(1),h(2),h(3))=i=1∏DP(vi(1)∣h(1))⋅j=1∏P(1)P(hj(1)∣h(2))⋅P(h(2),h(3))⎩ ⎨ ⎧P(vi(1)∣h(1))=Sigmoid{[Wh(1)→vi(1)]Th(1)+bi(0)}[Wh(1)→vi(1)]P(1)×1∈W(1)P(hj(1)∣h(2))=Sigmoid{[Wh(2)→hj(1)]Th(2)+bj(1)}[Wh(2)→hj(1)]P(2)×1∈W(2)P(h(2),h(3))=Z1exp{[h(3)]TW(3)⋅h(2)+[h(2)]T⋅b(2)+[h(3)]Tb(3)}
深度玻尔兹曼机( Deep Boltzmann Machine,DBM \text{Deep Boltzmann Machine,DBM} Deep Boltzmann Machine,DBM),它的概率图结构表示如下:

- 将神经网络与概率相结合的生成模型。
如:变分自编码器( Variational Auto-Encoder,VAE \text{Variational Auto-Encoder,VAE} Variational Auto-Encoder,VAE),它的概率图结构依然是混合模型(引入隐变量模型)的概率图结构。
生成对抗网络( Generative Adversarial Networks,GAN \text{Generative Adversarial Networks,GAN} Generative Adversarial Networks,GAN),其计算图结构表示如下: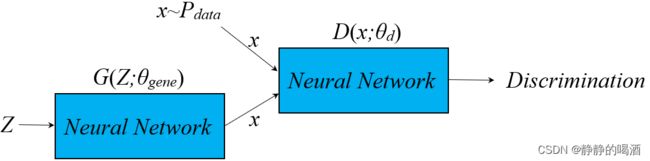
以及流模型( Flow-based Model \text{Flow-based Model} Flow-based Model)和自回归模型( Autoregressive Model \text{Autoregressive Model} Autoregressive Model)。
相关参考:
生成模型2-监督VS非监督