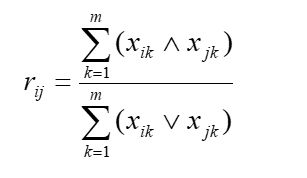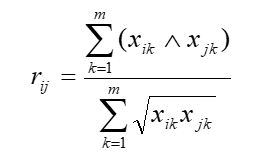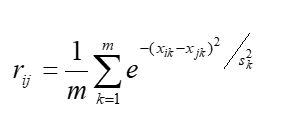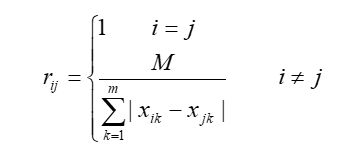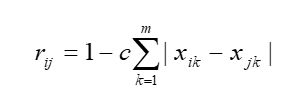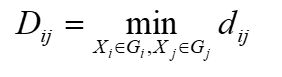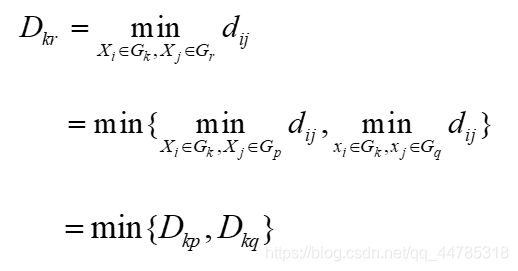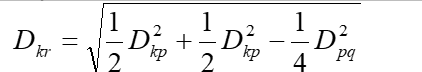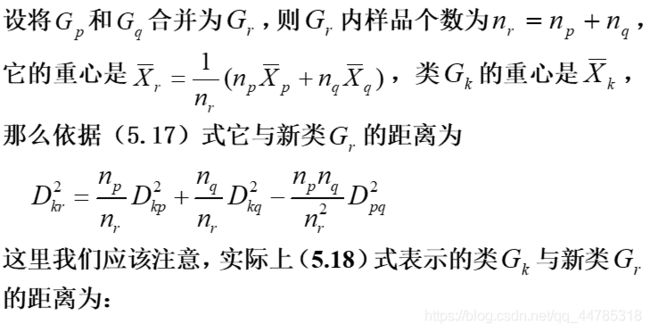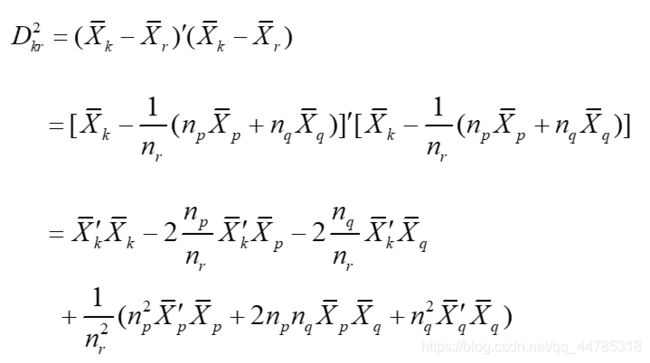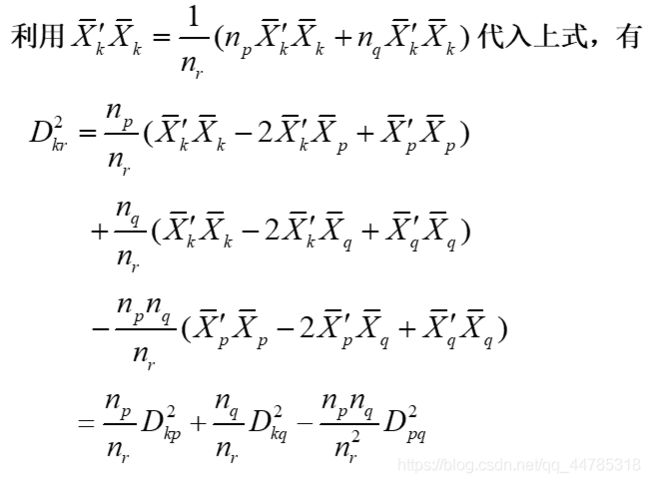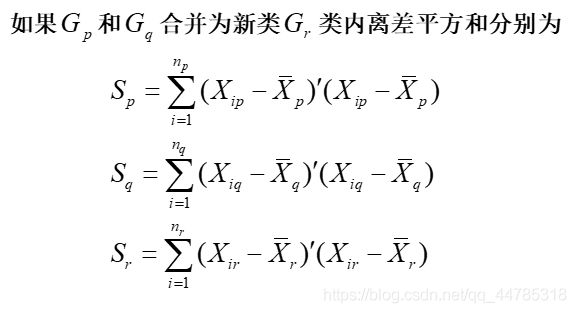Clustering Analysis -- 聚类分析
目录
相似系数度量:
1.数量积法
2.夹角余弦
3.相关系数
4.最大最小法
5.算数平均最小法
6.几何平均最小法
7.绝对值指数法
8.指数相似系数法
9.绝对值倒数法
10.绝对值减数法
11.非参数法
12.贴近度法
13.专家打分法
划分聚类方法(PAM)
K均值聚类分析
层次聚类方法
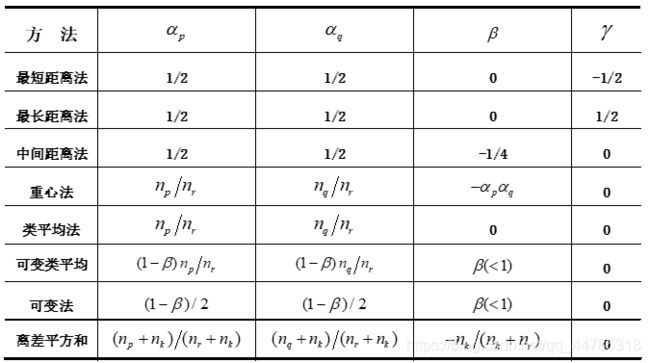
最小距离法(single linkage method)广泛采用的类间距离
最短距离法
最大距离法(complete linkage method)
类平均距离法(average linkage method)
中间距离法
重心法(centroid hierarchical method)
离差平方和(ward method)
类平均法
可变类平均法
可变法
离差平方和法
系统聚类法参数表
BIRCH算法
CURE算法
ROCK算法
基于密度的方法(density-based method)
DBSCAN算法
基于网格的方法(grid-based method)
STING算法
基于模型方法(model-based method)
COBWEB方法(model-based method)
AutoClass方法
聚类分析(cluster analysis)是将样品个体或指标变量按其具有的特性进行分类的一种统计分析方法。
典型的数据聚类基本步骤如下:
相似系数度量:
体现对象间的相似程度
1.数量积法
2.夹角余弦
3.相关系数
4.最大最小法
5.算数平均最小法
6.几何平均最小法
7.绝对值指数法
8.指数相似系数法
9.绝对值倒数法
10.绝对值减数法
11.非参数法
12.贴近度法
13.专家打分法
划分聚类方法(PAM)
是给定一个有n个对象或元组的的数据库构建k个划分的方法。每个划分为一个类(或簇),并且k<=n。
每个类至少包含一个对象,
每个对象必须属于而且只能属于一个类(模糊划分计算除外)。
使得一个聚类中对象是“相似”的,而不同聚类中的对象是“不相似”的
K均值聚类分析
(1)从n个数据对象随机选取k个对象作为初始簇中心。
(2)计算每个簇的平均值,并用该平均值代表相应的簇。
(3)计算每个对象与这些中心对象的距离,并根据最小距离重新对相应对象进行划分。
(4)转步骤(2),重新计算每个(自变化)簇的平均值。这个过程不断重复直到某个准则函数不再明显变化或者聚类的对象不再变化为止。
层次聚类方法
对给定的数据进行层次的分解
思想:一开始将每个对象作为单独的一组,然后根据同类相近,异类相异的原则,合并对象,直到所有的组合并成一个,或达到一个终止条件为止。
思想:一开始将所有的对象置于一类,在迭代的每一步中,一个类不断地分为更小的类,直到每个对象在单独的一个类中,或达到一个终止条件。
层次的方法缺陷一旦一个步骤(合并或分裂)完成,就不能被撤销或修正,因此产生了改进的层次聚类方法,如
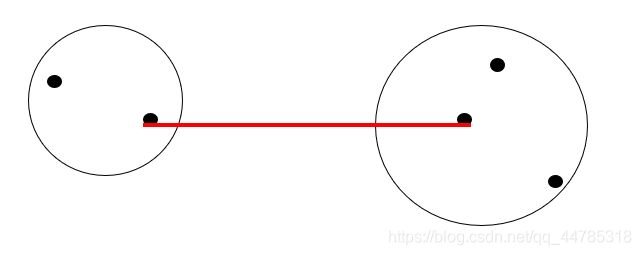
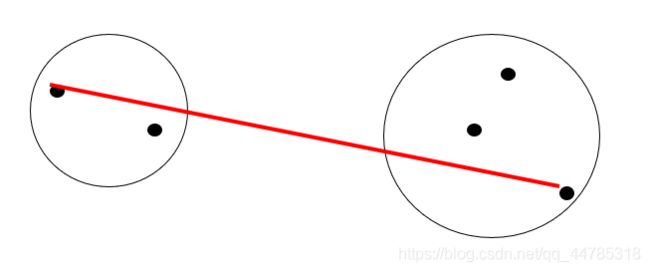
最小距离法(single linkage method)广泛采用的类间距离
l极小异常值在实际中不多出现,避免极大值的影响
最短距离法
定义类与之间的距离为两类最近样品的距离,即为
设类与合并成一个新类记为,则任一类与的距离为
(1)定义样品之间距离,计算样品的两两距离,得一距离 阵记为D(0) ,开始每个样品自成一类,显然这时Dij = dij。
(2)找出距离最小元素,设为Dpq,则将Gp和Gq合并成一个新类,记为Gr,即Gr = {Gp,Gq}。合并完距离最短的 选取 取这两个中到点的最短的那个
(3)按(5.12)计算新类与其它类的距离。
(4)重复(2)、(3)两步,直到所有元素。并成一类为止。如果某一步距离最小的元素不止一个,则对应这些 最小元素的类可以同时合并。
最大距离法(complete linkage method)
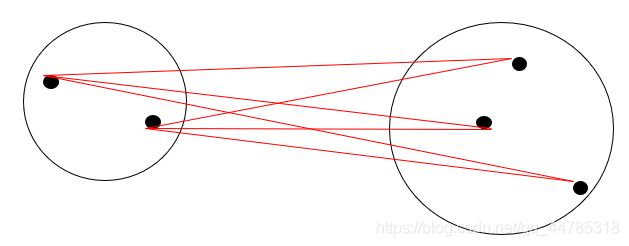
类平均距离法(average linkage method)
类平均距离法(average linkage method)类间所有样本点的平均距离
该法利用了所有样本的信息,被认为是较好的系统聚类法
中间距离法
最短、最长距离定义表示都是极端情况,我们定义类间距离可以既不采用两类之间最近的距离也不采用两类之间最远的距离,
而是采用介于两者之间的距离,称为中间距离法。
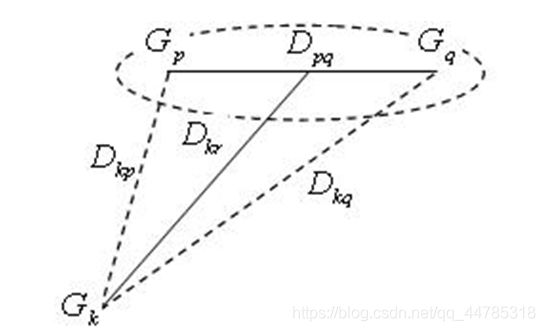
中间距离将类Gp与Gq类合并为类Gr,则任意的类Gk和Gr的距离公式为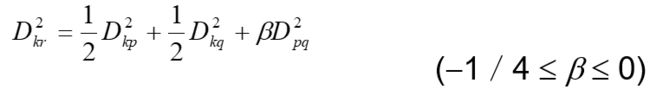
设Dkq>Dkp,如果采用最短距离法,则Dkr = Dkp,如果采用
最长距离法,则Dkr = Dkq。如图式就是取它们(最长距离与最短距离)的中间一点作为计算Dkr的根据。
l特别当b = - 1/4,它表示取中间点算距离,公式为
重心法(centroid hierarchical method)
l类的重心之间的距离
l对异常值不敏感,结果更稳定
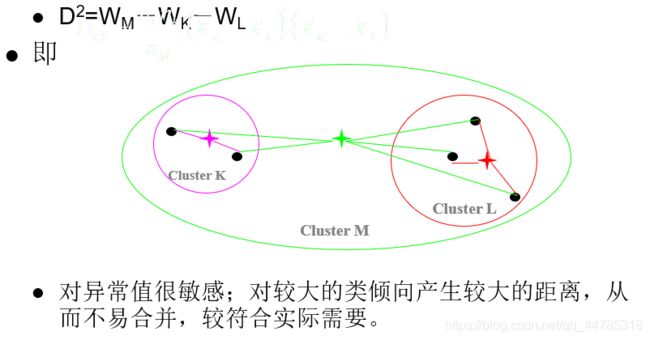
离差平方和(ward method)
类平均法
可变类平均法
可变法
离差平方和法
系统聚类法参数表
BIRCH算法
通过引入了聚类特征和聚类特征树概念,Zhang 等人提出BIRCH算法[Zhang et al. 1996] 。聚类特征是一个包含关于簇的二元组,给出对象子聚类的信息汇总描述。如果某个子聚类中有N个d维的点或对象,则该子聚类的定义为CF=(N,LS,SS),其中,N是子类中点的个数,LS是N个点的线性和,SS是点的平方和。聚类特征树中所存储的是关于聚类的信息,这些信息是计算聚类和有效利用存储的关键度量。每个叶节点包含一个或多个子聚类,每个子聚类中包含一个或多个对象。一个聚类特征树有两个参数:分支因子B和阈值T,分支因子B定义了每个非叶节点后代的最大数目,阈值参数T给出了存储在树的叶子节点中的子聚类的最大直径。BIRCH算法主要包括扫描数据库和聚类两个阶段。
(1)扫描数据库,建立一个初始存放于内存的聚类特征树,可以看作数据的多层压缩,试图保留数据内在的聚类结构。一个对象被插入到距其最近的叶节点(子聚类)中时,如果在插入对象后,存储在叶节点中的子聚类的直径大于阈值,那么该叶节点被分裂,也可能有其他节点被分裂。新对象插入后,关于该对象的信息向根节点传递。通过修改阈值,聚类特征树的大小可以改变。如果存储聚类特征树需要的内存大于主存的大小,可以定义一个较大的阈值,并重建聚类特征树。重建过程从旧树的叶子节点建造一个新树。这样,重建树的过程不需要重读所有的对象。因此为了建树,只需读一次数据。采用一些启发式规则和方法。通过额外的数据扫描来处理孤立点和改进CF树的质量。聚类特征树建好后,可以在阶段二被用于任何聚类算法
(2)BIRCH采用某个聚类算法对聚类特征树的叶节点进行聚类。B1RCH算法具有可伸缩性,算法的时间复杂度为O(n)(不重建聚类特征树时),通过对数据集的首次扫描产生一个基本聚类,二次扫描进一步改进聚类质量并处理异常点。BIRCH算法的处理速度较快,但对非球形簇处理效果不好。
CURE算法
CURE算法的时间复杂度为O(n),最大问题是无法处理分类属性。
ROCK算法
基于密度的方法(density-based method)
DBSCAN算法
基于网格的方法(grid-based method)
STING算法
基于模型方法(model-based method)
COBWEB方法(model-based method)
AutoClass方法