基于Java机器学习自学笔记(第81-87天:CNN卷积神经网络的入门到全代码编写)
注意:本篇为50天后的Java自学笔记扩充,内容不再是基础数据结构内容而是机器学习中的各种经典算法。这部分博客更侧重于笔记以方便自己的理解,自我知识的输出明显减少,若有错误欢迎指正!
目录
1. CNN的基本概念
1.1 CNN的诞生环境
1.2 传统全连接神经网络的不足
1.3 卷积(Convolution)
1.4 池化(Pooling)
1.5 卷积的神经网络的权值共享与限制连接
1.6 卷积的神经网络的处理流程
2. 卷积的神经网络的学习过程
2.1 确立参考模型
2.2 forward
2.3 backPropagation: 计算惩罚信息
2.3.1 基本原理
2.3.2 Output Layer
2.3.3 Pooling Layer与反卷积
2.3.4 Convolution Layer与反池化
2.4 backPropagation: 更新边权
3. 卷积的神经网络代码实现总思路梳理
4. 底层代码: Dataset类与Size类
4.1 Dataset类
4.2 Size类
5. 关键的运算代码: Operator接口 与 MathUtils类
6. CNN框架代码: CnnLayer类与LayerBuilder类
6.1 CnnLayer类与其成员变量解释
6.2 LayerBuilder类
7. 核心代码: FullCnn类
7.1 成员变量与初始化
7.2 训练
7.3 forward预测
7.3 backPropagation设置惩罚信息
7.4 更新边权与偏差
8. 运行效果测试
1. CNN的基本概念
1.1 CNN的诞生环境
卷积神经网络(Convolutional Neural Networks, CNN)是神经网络在图像数据方面表现得最佳的方案. CNN相比于之前我了解的BP神经网络, 其通过卷积求权与"权共享"的方案极大削减了一般神经网络的算法的开销, 具有兼容深度学习以及更高维数据(特别是图像)的显著优势.
理论上来说, 参数越多的模型复杂度越高, "容量" 越大, 同时也能胜任更复杂的学习任务. 早期因为计算机算力的限制与有限数据的过度计算导致的过拟合, 使得科学家们没法完全去研究与解析高复杂度的神经网络结构. 而如今随着云计算, 大数据时代的到来, 以" 深度学习 "为代表的复杂模型开始逐步受到人们的青睐, 很好适配了当前逐步提高的算力与数据时代. 而典型的应用于多特征的复杂深度学习案例就是图像的神经网络
1.2 传统全连接神经网络的不足
图像的数据量是很大的, 之前我们采用的iris数据集不过是4个特征属性与3个标签, 但是图标是像素级别的, 哪怕是一张100*100的小图, 它的神经元就能达到100, 000. 这是单层的信息元数量, 如果采用全连接神经元, 那么两层就可与达到10\(^{8}\), 这已经逼近计算机的常规算力极限了. 此外, 对图像采用全连接还有以下不足:
- 图像展开为向量会丢失空间信息: 多维数据的组合本身在逻辑上就不能利用常规的低维特征去代表, 就算利用某些数据结构手段去代表还是会有不足.
- 大量的参数也很快会导致网络过拟合
因此急需要设计一种适合于图像数据连接方案.
1.3 卷积(Convolution)
首先我们可以试着去思考图像识别的一些关键因素. 首先图像的识别本身是一种特征识别, 二维的特征其实相比一维的特征, 某种意义上人能更快接收并接受. 因为人的目光所见"引入脑海" 皆是二维, 我们很熟悉这些特征.
首先, 假如说我们看到一张熟悉的图片, 我们没必要全图一个一个找信息去验证这个事物究竟是什么, 往往我们只需要一部分的特征就好就好. 例如下面这只狗, 只要我们第一眼看到了狗头我们就能直接判断出这是一只狗.
因此整张图片的重要特征就是这个狗头, 因此关于这张图片的内容我们可以用一个很小的pattern来代替就好了(如下图), 要会关注特征而非全图信息, 把目光放到图像的关键pattern上即可. 而往往来说, pattern的大小要远小于图片的大小.
另外图像特征出现的位置也不总是固定, 它可能在图像中的任何可能的位置, 可能是middle, upper-right, lower-left等等. 但是现实中对于狗的识别过程中不可能分别训练出专门识别狗头在upper-right的网络以及适用于狗头在middle的网络.(上面的狗头在upper-right, 而下面的狗头在middle-left)
最后, 二维图像的清晰与否有时对于特征来说也许没那么重要. 有些常年与狗打交道的人, 如果年老后视力衰退得路都看不清了, 但是看见了自家小狗的脑袋的模糊轮廓还是能很快辨别出来的. 这就是特征数据在亏损环境下仍然具有的代表性. 比如下面这条像素删去大部分的狗狗相信大部分人都还是能看出来吧? 但是这张图片却只有原图的1/16那么大.
总结来看图像识别应当具有以下三种特征
- 图像的识别应该是特征的识别, 重点应该放在特征的提取与重点特征识别
- 图像的特征应该是全方位的, 重要的特征会在任何可能的地方出现
- 图像在像素亏损情况下仍然可以很大程度上保留特征
针对上面1,2点, 我们提出了卷积(Convolution)
现在有下面这样的一张二值图:
可以发现这张二值化图像中存在个别非常明显的斜向纹理或者竖向纹理, 因此我们可以模仿这样的基础纹理构造两个过滤器:
这里提供的两个过滤器本身就是一个比原图更小的两个矩阵, 但是这两个矩阵特化了最小的特征元, 比如说横向或者斜向特征. 而在实际操作时就像一个掩码一样, 其所覆盖的图片区域(这个区域就是CNN中的感受野)能够滤出符合过滤器自身的信息.
具体操作就是通过过滤器进行简单的二维内积, 如果说信息完全吻合, 那么就会得到最大的权. 一旦有信息不对称就会出现(-1 * 1)的可能从而造成扣分, 或者信息缺失(1 * 0)不算分.如此的操作就可以实现解决我们总结的图像特征的第一点.
那么怎么保证所有区域都能识别呢 , 只需要将我们的过滤器在全图进行遍历就好了. 我在网上找到了一个GIF图, 可以很好说明这个过程:
上面这个GIF图通过3*3的过滤器, 在5*5的Image上以步长(stride)为1的方式遍历得到了一个(5-3+1)*(5-3+1)的矩阵, 这个矩阵就是特征映射(Feature Map). 这个Map其实就相当于是我们图像上与这个过滤器有关的特征的集成与表示, 若说原图是由若干神经元构成的, 那么新的Map的每个神经元就代表了Image中某个感受野(receptive field)内的全部神经元. 继续理解, 通过Feature Map最高值出现的坐标我们就可以在原image上准确定位到可靠的特征区域, 而不需要专门去设计针对不同位置的特征学习机, 只需要设置这个特征的过滤器就好了(下图所示)
这就回应了图像识别应当具有的第2种特征. 综上就提出了对于图像问题采用的神经元连接的新手段----- 卷积(Convolution)
额外提两句: 有时我们也会通过全零填充(Zero-Padding)来保证Feature Map与原Image的大小一致.
而且上面进行卷积操作过程中, 实际上步长也可以设置得更大一些. 一般来说步长比较小时会"慢慢地"对于内容提取特征, 属于细粒度的, 得到特征也比较多, 但是速度会慢一些; 而步长比较大时会粗粒度地去提取, 导出的Feature Map空间会更小, 利于快速获得最终特征, 但是它提取的特征会少一些, 不那么丰富, 甚至存在部分的信息丢失的代价(因为边缘部分可能无法与步长构成一个符合过滤器的视野大小). 往往来说对于图像数据采用stride = 1足矣, 更高的步长更多用于文本数据
综上有一个求解Feature Map的简单启发式公式, 譬如说空间上的三维输入体是\(W_1 \times H_1 \times D_1\), 而卷积层中感受野范围为\(F \times F\), 步长有stride = \(S\), 卷积核数量有\(K\), 零填充数目为\(P\), 可得输出体(Feature Map)\(W_2 \times H_2 \times D_2\)的尺寸细节有:\[\begin{array}{c}
W_{2}=\left(W_{1}-F+2 P\right) / S+1 \\
H_{2}=\left(H_{1}-F+2 P\right) / S+1 \\
D_{2}=K
\end{array} \tag{1}\]
其实如果希望得到的Map要更小, 我到觉得没必要如此手段了啦, 我们往往更常用另一种手段.
1.4 池化(Pooling)
池化其实非常简单, 它的目的就是完成上述总结的图像识别应当具有三种特征之三----图像压缩减. 图像压缩有非常多的手段, 有的人会用消除坐标为奇数像素点, 或者单纯比例缩放. 当然这些手段都显得粗暴, 实际我们会将原image进行区域分割并且在每个区域内有选择地" 挑选 "像素点.
最常用的一种池化就上最大池化(Max Pooling). 如果最大池化使用的过滤器是2*2, 那么他的目标就上将原图的长压缩为原来的1/2, 宽亦如是, 体现在操作上就是将图像分为4个组, 然后在每个组内选择最大的特征神经元来代表这一组, 这样每个组内就损耗了3/4的像素信息, 推广到整个图就压缩到原来的1/4.
其实池化最开始并不是只有最大池化, 还有平均池化等操作, 但是随着CNN的发展, 人们发现特征值中那些最大的反而是最重要, 因此每次筛选都挑选最大的能最大程度地保持一个区域的代表性. 而平均池化本质上是削减了一个区域的代表性, 因此渐渐就很少见到使用平均池化的方法了, 最大池化也就成为了池化的代名词.
1.5 卷积的神经网络的权值共享与限制连接
卷积作为连接方式的网络就是CNN, CNN的网络连接直观来看是全连接类似, 但是在细节之处却又很大差异
每一层所描述的单个结点并不是一个单纯的数值, 而是一个二维的平面, 每个平面都是由若干个神经元所构成的神经元阵列, 而单个卷积层又由多个平面通过叠加构成. 你可以将这个多个平面形成的三维结构理解为面包, 而每个平面都是一个小切片(slice), 切片个数构成了深度(depth). 每个深度切片分别与\(n\)个卷积核进行卷积操作得到\(n\)个Feature Map. 假若一个卷积层的深度为3, 那么通过卷积操作就会得到3个平行的\(n\)维Feature Map切片组合(图中为了方便只画了2个深度大小, 只有n=4个卷积), 最后将这3个平行的\(n\)维Feature Map切片组合进行合并, 从而得到了新的深度为\(n\)的卷积层. 总的来说, 只要记住: 一个卷积核对应一个Feature Map切片,有多少个卷积, 就会生成多少个Feature Map切片. 输入源的不同切片通过同个卷积核得到的不同Feature Map最终都会叠加为一个Feature Map切片(图中下面网络中的浅棕色与棕色方块通过叠加变成了一个深棕色方块 就描述的这个过程).
这个过程中我只给出了输入/输出层, 卷积层的操作, 实际上卷积层总共可以细分为 输入\输出, 卷积层, ReLU层, 池化层(更好的翻译为"汇聚层", 但是意思都是一个意思), 全连接层. 但是在实际设置中, 卷积层与ReLU层是作为一个整体而存在的, 卷积操作的末尾其实都会执行一次激活函数进行学习(至于为什么ReLU呢? 一方面ReLU计算量足够小, 而且ReLU的特性优点非常适用于CNN), 而池化层相对因为是使用固定的函数处理, 都很容易实现.
这样的CNN网络的学习过程有什么逻辑解释呢. 其实你可以把这个过程理解为图像整合与细化的过程, 最开始的输入层是图像的全貌, 但是卷积核本身只能承载简单的特征元, 他是非常微小的. 因此最开始获得的第一层卷积层都是图像的基础特征的表示, 比如是对于图中某种斜线的表示, 或者是某种色彩的占比, 只要图像中存在这种占比, 这样的分类器就能被激活. 第一层提供的识别出来的特征元通过网络的复合导致了第二层更复杂特征, 第二层卷积层就可能是一些木质纹理, 多层纹路等等, 第三层再通过累加可能就是人脸, 轮胎, 蜂窝型等等(绝不是说学习到这一层后它学习得到的图像就是长这样的, 只是说其承载的特征可以用于描述这样的事物, CNN越往后学习, 图像的空间大小是缩小的, 不可能越来越清晰).
为什么说卷积实现的效率要比单纯的全连接神经网络的效率要出众呢?
回忆下BP神经网络的构造, 我们每个隐层的神经元无一例外地同它前面的所有神经元构成连接, 属于全连接的神经网络. 假设初始图像抽象为3 * 32 * 32的输入, 若对它用全连接网络, 那么第一个卷积层中某个Feature Map的某个像素神经元需要与输入层的3* 32 * 32个像素神经元建立全面连接才行. 那么CNN是怎么对待这个问题的呢?
我比较喜欢台大的李宏毅教授讲CNN时用的这个图来解释:
上图中6*6的image是输入层的一层切片, 而4*4的结构是通过3*3的卷积核按照步长为1卷积操作得到的一层Feature Map切片. 在一次卷积操作后, 这个Map中的第一个像素神经元实际代表了6*6的image左上3*3的感受野的全体数据. 见下图, 如果携以立体的目光, 假如源image共有3个如此的切片, 那么这个Map中的这一个像素神经元只连接了 3 * 3 * 3 的神经元而并非全连接的6 * 6 * 3
更进一步, 可以像上图那样将二维图像逐行拆开平铺为36个结点, 其实很容易注意到: Feature Map中的某个神经元只映射了6个结点. 所以CNN是能使用更少地参数去映射!
当执行另一个相邻区域的映射的时候, 它使用的源image中的神经元与第一个区域存在重叠, 这是由卷积操作的步长遍历特征决定的. 同样地将二维图像逐行拆开平铺为36个结点, 可以发现Feature Map中的每个神经元在使用相同的权值(因为同个Feature Map的卷积核是一样的), 而且同一个权边在不同的Feature Map神经元中参与映射的结点都是不同的.
综上所述, CNN同个限制每个Feature Map神经元映射的结点数目以及每个神经元共用一致的权边体系, 从而极大减少了参数的数量. 换做是全连接神经网络来模仿上面的图, 如果输入节点是36个, 然后第一个隐层结点是16个, 那么就需要一共16 * 36个各异的权边, 但是这图中若采用CNN却只有区区9个不同权边. 而且若真的把平面像素平铺开来, 其二维的特征还会被破坏, 可能效果远不如这9个有二维关系的网络 !
综上, CNN的边权共享与限制连接 造就了它优于全连接神经网络的效率与准确度.
1.6 卷积的神经网络的处理流程
简单以一个例子说明CNN运作的全过程.
以一个1*32*32的手写体为例, 最开始我们采用6个5*5的卷积核对这1张图片进行处理, 因为一个卷积核管理生成卷积层的一个映射分片, 所以最终我们得到了6张Feature Map. 而通过卷积的5*5空间循环遍历最终Feature Map的大小就削减为28*28(32 - 5 + 1). 进一步为扩大图像削减的速度, 进行完一次卷积操作后续就执行了一次池化得到了采样层6张14*14的池化层.
后续仿照这样的操作, 第二次卷积时使用16张5*5的卷积核进行卷积得到了16 * 10 * 10的Feature Map, 然后通过池化削减为16 * 5 * 5.
最后的卷积操作提供了120张5*5的卷积核, 通过卷积得到了120 * 1 * 1的卷积层, 然后将这120个1*1的像素点flatten为一个1*120的向量, 构成全连接网络部分的输入端口, 然后后续通过末端的全连接网络将这120个输入的结点转换为10个输出. 而这10个输出中的最优值就是我们需要的手写体含义.
这个过程需要明白的就是:
- CNN本身虽然通过非全连接的手段提取了图像的特征点, 但是在CNN的末端仍然具有全连接的部分. 我们对图像进行卷积的目的终究是" 提取特征 "而并不是" 解析特征 ".
- 有些图中将卷积层和ReLU层分开描述了, 但是实际上可以将ReLU认为是卷积层的子操作, 卷积操作的末尾其实都会执行一次激活函数进行学习. 所以可以认为上图将ReLU隐含了.
- CNN的设置是灵活, 并不一定说1次卷积1次池化, 2次卷积配套1次池化也是可取的, 总之CNN本身就有许多网络架构(Alexnet, Vgg, ...), 具体问题具体分析, 具体学习.
- 非全连接段与全连接段的界限并不确定, 有的方案会在最终采样的Feature Map切片大小为1*1时进行flatten; 有的方案可能在切片大小在某个足够小时就进行flatten, 将某个m*k*k大小切片flatten为m*k²个全连接神经网络的输入结点, 或者最后直接池化m*1*1.
- 第一次卷积操作时, Feature Map中一个像素神经元只映射手写图中的1*6*6区域, 但是到第二次卷积时, Feature Map中一个像素神经元映射变为六张6*6的感知野范围, 这是因为它之前的池化层(采样层)是由六层切片构成, 而切片一个就有一个6*6的感知野. 因此Feature Map中一个像素神经元就承载了6*6*6个信息空间
2. 卷积的神经网络的学习过程
2.1 确立参考模型
CNN作为一个神经网络, 其网络参数并非凭空产生, 它也需要一个完成的网络学习过程. 实际上CNN的学习过程与BP神经网络非常类似, 都是由一个前向的forward获得预测与逆向backPropagation进行惩罚信息更新与调整边值.
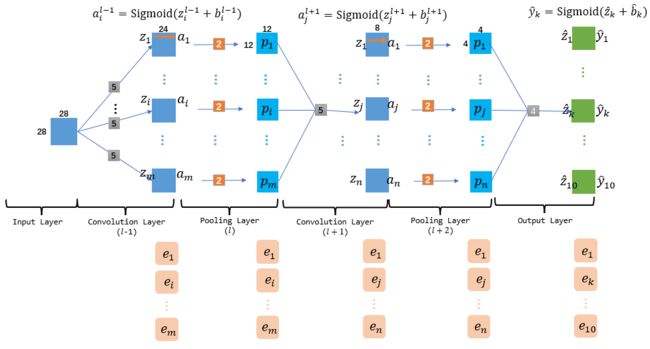
为了方便基础的公式解释与代码编写, 这里对于CNN的众多部件进行简化.如图, 这个CNN的输入数据是一张28*28的手写字体图(二值化的, 因此一张足矣), 然后在输出时省略全连接部件, 直接在CNN结束时输出1*1的矩阵, 其中最大的矩阵下标就是我们找寻的手写字的文字. 同时, 因为这个案例没有面向全连接层, 因此最后输出层并没有进行flatten, 而是模仿卷积层, 利用上一个池化层等大的卷积核进行卷积得到1*1的矩阵, 用这个矩阵直接代表最终结果.
同时我们定义的一个layer的范围是这个layer表示的切片数值集本身以及其相关的左侧边结构, 如此来说上图就有6个layer, 其中只有Input layer范围内没有边结构. 同时, 卷积层相关的左侧边权是一个个小的卷积核(图中灰色小矩阵), 但是池化层左侧边主要是池化用的比例核(橙色小矩阵). 而输出层因为没有采用flatten, 因此本质上输出层就是一个卷积层, 不同的只是它的卷积核大小要与上层池化层的矩阵大小一致, 从而保证卷积操作后得到是1*1的矩阵. 记住这个图, 后面我们forward与backPropagation都将基于此图描述.
CNN中可以忽略全连接部分? 当然可以. 刚刚提到过, CNN是灵活的, 全连接层的主要作用就是将前层计算得到的Feature Map 样本进行学习, 最终特征表示整合成一个值. 对于某些特征简单的内容, CNN输出的特征值量级只要能控制在合理范围, 不全连接也是可以的.
倘若需要补充全连接层的话, 建议最终采用交叉熵损失来作为最终的损失函数度量, 同时利用激活函数Softmax来作为全连接层末端的激活函数, 同时全局采用ReLU来作为激活函数, 这是CNN的一套标准流程(详情学习与了解可以跳转到这个网址). 而本文计划采用喜闻乐见的均方误差损失:\[E=\frac{1}{2} \sum_{j=1}^{l}\left(\hat{y}_{j}-y_{j}\right)^{2} \tag{2}\] 以及Sigmoid来实现这个过程 ( 毕竟我熟悉~ 详情可见我写的BP神经网络的博客, 里面就是这套流程 ), 当然缺陷就可能会慢一些. Sigmoid与均方误差的一些基本概率我就不再赘述, 而关于激活函数的介绍可见我的这篇博客.
2.2 forward
forward的过程比较简单, 核心来说就是1.6中提到的那些过程, 正向传播主要进行每一层结果的预测, 这个过程相比BP不同的基本来说就主要是结果是矩阵形式而非数值, 得到每层信息是一个三维的张量(tensor), 而非二维的向量(vector).
假设我们输入的图片为\(I\), 初始采用\(m\)个卷积核\(K_i\), 得到一个基本卷积集合\(\{K^{1}_{1},K^{1}_{2},...,K^{1}_{m}\}\). 这里描述的1是说明层下标为\(l=1\)(层从0开始, 但是输入层没有描述的必要) 因此生成的第二层Feature Maps为:\[\left\{\begin{array}{c}z_{i}^{1}=\operatorname{conv}\left(I, K_{i}^{1}\right) \\a_{i}^{1}=\text {Sigmoid}\left(z_{i}^{1}+b_{i}^{1}\right) \\i=1,2, \ldots, m_{1}\end{array}\right.\] 其中的\(a^{1}_{i}\)表示一个平面, 即一个Feature Map, 这里的\(b\)是一个偏差值,他的个数与函数输出所在的层的切片个数是一致的, 你可以将其理解为类似于MP神经元中的阈值, 因此CNN中我们不再讨论哑结点. 在CNN中我们计算激活函数时是面向矩阵的, 但是依旧适用, 实际计算时矩阵中每个神经元都是Sigmoid的自变量, 带入计算得到因变量然后组成目标矩阵. 下面的Pooling Layer没有激活函数, 因此只用一个下采样(其实就是池化, 下采样的目的就是压缩) 即可得到第一个池化层(第2层)的参数表示表示: \[\left\{\begin{array}{c}
p_{i}^{2}=\text {downsample}\left(a_{i}^{1}\right) \\
i=1,2, \ldots, m
\end{array}\right.\] 然后到达第3层的卷积层还需要一次卷积操作, 但是这里卷积过程要公式表示就要稍微麻烦一些了, 因为上个池化层有\(m≠1\)个结点, 因此需要依次遍历\(m\)结点并分别与某个卷积核\(K^{3}_{i}\)卷积, 最后相加叠加得到\(z^{3}_{i}\). 有下面的Feature Maps表示:\[\left\{\begin{array}{c}
z_{i}^{3}=\sum_{j=1}^{m}\left[\operatorname{conv}\left(a_{j}^{2}, K_{i}^{3}\right)\right] \\
a_{i}^{3}=\text {Sigmoid}\left(z_{i}^{3}+b_{i}^{3}\right) \\
i=1,2, \ldots, n
\end{array}\right.\] 最后一个池化层有得到Feature Maps的参数过程:\[\left\{\begin{array}{c}
p_{i}^{4}=\text { downsample }\left(a_{i}^{1}\right) \\
i=1,2, \ldots, n
\end{array}\right.\] 最后一个输出层有得到Feature Maps过程(上面已经分析过了卷积层与输出层的异同, 基本的有\(K^{5}\)的尺寸与任意\(p\)一致):\[\left\{\begin{array}{c}
\hat{z}_{k}=\sum_{j=1}^{n}\left[\operatorname{conv}\left(p_{j}^{2}, K_{k}^{5}\right)\right] \\
\hat{y}_{k}=\text {Sigmoid}\left(z_{k}^{3}+b_{k}^{5}\right) \\
i=1,2, \ldots, 10
\end{array}\right.\] 最终输出的tensor \(\mathbf{\hat{y}}\)就是我们的最终预测, 一般的CNN到这里可能要将tensor给flatten为一个向量(vector)并进行全连接, 但是本CNN特征少, 而且最终输出时有意将平面转化为1*1的矩阵, 所以从数组角度来说, 这里得到的tensor其实就是一个向量, 只不过在代码中我们可能需要专门进行三维到二维的转化过程罢了, 这个在代码中在细聊吧. 总而言之, \(\underset{0 \leq i \leq 10}{\arg \max }\mathbf{\hat{y}}\)的值就是我们对于手写28*28的数值的预测了 !
2.3 backPropagation: 计算惩罚信息
2.3.1 基本原理
backPropagation永远是神经网络中最充满数学气息的地方, 博主撰写此文亦是首次接触CNN, 数学功底欠佳, 多有步骤参考网络, 一些证明理由和数学意义的卷积结论多直接使用, 愿诸位名士多加指正, 借以完善充盈.
阅读下问描述建议有过BP神经网络的知识作为储备(包括基础的激活函数Sigmoid与均值损失函数), 再度安利~ 可见我的博客~~
CNN的backPropagation本质上同BP神经网络别无二致, 首先要进行惩罚信息的更新, 其次再完成依据惩罚信息更新边权. 首先从后往前开始, 由公式2可得损失函数为\(E\), 而通过BP算法中得到的启发, 在我们按照梯度下降原理对\(E\)根据边权求偏导后, 通过链式法则分解后, 总是能分解出对结点求偏导的部件. 我们习惯上总是将这些部件分割出来, 比如说西瓜书上用的\(g\), \(e\)分割表示. 为何单独表示呢? 因为这些部分的内容总是前后关联, 需要采用类似于动态规划的迭代思路步步求解, 因此把它们从庞杂的链式偏导中专门拿出成体系地表示一来方便理解, 一来利于代码实现. 而逻辑上, 我们更喜欢称之为" 惩罚信息 ", 下面我将统一用\(e\)来表示这些内容(在CNN中, 很多文章中喜欢用\(\delta\)来表示这家伙)
数目上, 每层的成分信息总是与其结点个数一致, 并且与层的形式相关, 比如CNN中的所有惩罚信息都是矩阵, 而且矩阵尺寸都是与其所表征的层的切片尺寸一样. (下图中Input Layer无需惩罚信息, 因为它没有前导边的更新)
2.3.2 Output Layer
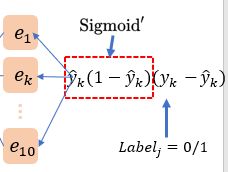
首先, 损失函数\(E\)对Output Layer的结点集\(\mathbf{\hat{z}}\)求偏导:\[\begin{aligned}
e_{k}^{l+3} &=\frac{\partial E}{\partial \hat{y}_{k}} \cdot \frac{\partial \hat{y}_{k}}{\partial \hat{z}_{k}} \\
&=\left(\hat{y}_{k}-y_{k}\right) \cdot f^{\prime}\left(\hat{z}_{k}+\hat{b}_{k}\right) \\
&=\hat{y}_{k}\left(1-\hat{y}_{k}\right)\left(y_{k}-\hat{y}_{k}\right)
\end{aligned} \tag{3}\] 这里利用里Sigmoid导函数的特性: \(f^{\prime}(x)=f(x)(1-f(x))\). 这个3式中的实例图如下:
2.3.3 Pooling Layer与反卷积
Pooling Layer的后面一定是Convolution Layer, 损失函数\(E\)对\(l+2\)层的Pooling Layer结点集合\(\mathbf{p}^{l+2}\)进行求导, 虽然说\(\frac{\partial E}{\partial p^{l+2}_{j}}\)不可知, 但是\(\frac{\partial E}{\partial \hat{z}_{k}}\)通过式3是已知的, 我们可以借用其作为已知量穿插到链式偏导中. 同时, 在forward过程中, 任何一个获得的\( \hat{z}_{k}\)都是当前所有\(\mathbf{p}^{l+2}\)各自卷积再求和得到的, 反过来backPropagation时, 任何一个\(p^{l+2}_j\)都是当前全部的\(\mathbf{\hat{z}}\)的共同影响因子, 因此逆向\(E\)对\(p^{l+2}_j\)求导时, 依据链式法则, 必须走10个相关的\( \hat{z}_{k}\)变量共同到此, 然后结果相加. 最终得到下面的推导:\[\begin{aligned}
e_{j}^{l+2}& = \frac{\partial E}{\partial p^{l+2}_{j}}\\
&= \sum^{10}_{k=1}\frac{\partial E}{\partial \hat{z}_{k}} \cdot \frac{\partial \hat{z}_{k}}{\partial p^{l+2}_{j}} \\
&= \sum^{10}_{k=1} e_{k}^{l+3} * \operatorname{rot180°}(K_{jk}^{5})\\
\end{aligned}\tag{4}\]
(注: 上述公式中的*为full模式的卷积)
咦?最后那个转换是如何得到的呢, 实际上是因为单独求\(\frac{\partial\hat{z}_{k}}{\partial p^{l+2}_{j}}\)是求不出的, 必须结合另一种卷积公式:\[e^{l} \frac{\partial z^{l}}{\partial p^{l-1}}=e^{l} *\operatorname{rot} 180^{\circ}\left(K^{l}\right) \tag{5}\]
(注: 上述公式中的*为full模式的卷积)
这个公式就是卷积的偏导, 它又叫做"反卷积". 关于反卷积的数学证明详见可以查看这篇文章的3.4部分: 卷积神经网络(CNN)模型结构,前向传播算法和反向传播算法介绍![]() https://blog.csdn.net/anshuai_aw1/article/details/84747934 我在后续讲的边权更新时会再度用到和链接中类似的方法, 这里就不赘述了, 听懂了后面我写的那部分, 这里大家自己都可以试着自行推导.
https://blog.csdn.net/anshuai_aw1/article/details/84747934 我在后续讲的边权更新时会再度用到和链接中类似的方法, 这里就不赘述了, 听懂了后面我写的那部分, 这里大家自己都可以试着自行推导.
要格外主要公式4中的卷积操作并不是我们最初介绍什么是卷积时提到那个卷积(Valid卷积). 假设最开始上层的切片大小为28*28, forward中通过了5*5的卷积核之后: (28-5+1)*(28-5+1) 变为 24*24. 但是作为backPropagation逆操作, 我们需要保证24*24通过这个5*5的卷积核变回28*28. 这就要用到本文1.3中提到的全零填充(Zero-Padding). 为什么是全零填充呢? 这个就要先了解一下上面给出链接的文章中的反卷积求法了, 按照那个求法, 最终我们会得到一个等式组, 那个等式组转换为卷积形式后刚好原切片外围会套上一层0. 这也解释了为何套上0可以保证卷积操作可以避免尺寸损失.
*那么这个0要套多厚呢?*
我想用一个初中数学方法来解释这个问题~. 首先毋庸置疑, 在forward时, 若步长为1, 也没有填充, 通过公式1, 某个池化层切片到卷积层时存在下面这样的数学变换 \(n^2 \circ F^2 = (n-F+1)^2\), 这里\( \circ\)是一个假定的运算符, 表示前后两个平方式表示的矩阵做Valid模式的卷积运算后得到的矩阵平方式(这里的Valid模式卷积运算就是常规的做完尺寸会减少那种卷积). 设这个Valid卷积结果矩阵有\(G^2 = (n-F+1)^2\).
在进入backPropagation后, 我们需要将\(G\)阶矩阵的尺寸扩大为\(n\)阶. 于是给\(G^2\)大小的矩阵外层套上一个厚度为\(x\)的零边框, 现在这个矩阵尺寸变为\((G+2x)^2\), 然后再将这个尺寸的矩阵与\(F^2\)卷积核做Valid模式的卷积, 我们希望有 \((G+2x)^2 \circ F^2 = n^2\)的结果, 因此解\(x\):\[\begin{aligned}
(G+2x)^2 \circ F^2 &= n^2 \\
(n-F+1+2x)^2\circ F^2&=n^2\\
n-F+1+2x-F+1 &= n \\
x &= F-1
\end{aligned} \tag{6}\] 至此我们得到了一个关键的结论, \(A\)矩阵与尺寸为\(F^2\)的卷积核做常规Valid卷积运算得到\(C\)矩阵后, 只要给\(C\)矩阵套上一个宽度为\(F-1\)的零边框, 然后再与尺寸为\(F^2\)的卷积核做常规Valid卷积运算, 就可以还原\(A\)矩阵的大小. 这就是Full模式的卷积运算.
用图来验证想法将会更直观:
注意, Full模式的卷积操作只是尺寸还原, 无法做到值还原!
2.3.4 Convolution Layer与反池化
Convolution Layer的后面一定是Pooling Layer, 首先, 损失函数\(E\)对Convolution Layer的结点集\(\mathbf{z}^{l+1}\)求偏导. 虽然\(\frac{\partial E}{\partial z^{l+1}_{j}}\)不知, 但是\(\frac{\partial E}{\partial p^{l+2}_{j}}\) 可知, 老样子通过链式求导法则, 我们将它插入到链式偏导式中, 得到:\[\begin{aligned}e_{j}^{l+1}& = \frac{\partial E}{\partial z^{l+1}_{j}}\\&= \frac{\partial E}{\partial p^{l+2}_{j}} \cdot \frac{\partial p^{l+2}_{j}}{\partial z^{l+1}_{j}} \\\end{aligned}\] 而\(\frac{\partial p^{l+2}_{j}}{\partial z^{l+1}_{j}}\)可以分别拆开为\(\frac{\partial p^{l+2}_{j}}{\partial a^{l+1}_{j}}\)与\(\frac{\partial a^{l+1}_{j}}{\partial z^{l+1}_{j}}\)的乘积. 值的注意, 这里\(p_{j}^{l+2}\)到\(a_{j}^{l+1}\)的过程是直线的, 因为池化是一对一的, 没必要求和. \(p_{j}^{l+2}\)到\(a_{j}^{l+1}\)是Sigmoid的导数. 最终得到公式推导: \[\begin{aligned}
e_{j}^{l+1}& = \frac{\partial E}{\partial z^{l+1}_{j}}\\
&= \frac{\partial E}{\partial p^{l+2}_{j}} \cdot \frac{\partial p^{l+2}_{j}}{\partial z^{l+1}_{j}} \\
&= \frac{\partial E}{\partial p^{l+2}_{j}} \cdot \frac{\partial p^{l+2}_{j}}{\partial a^{l+1}_{j}} \cdot \frac{\partial a^{l+1}_{j}}{\partial z^{l+1}_{j}}\\
&= e_{j}^{l+2} \cdot \frac{\partial p^{l+2}_{j}}{\partial z^{l+1}_{j}} \cdot f^{\prime}(z_{j}^{l+1} + b_{j}^{l+1})\\
&= \operatorname{upsample}(e_{j}^{l+2})\cdot (1-z_{j}^{l+1})z_{j}^{l+1}\\
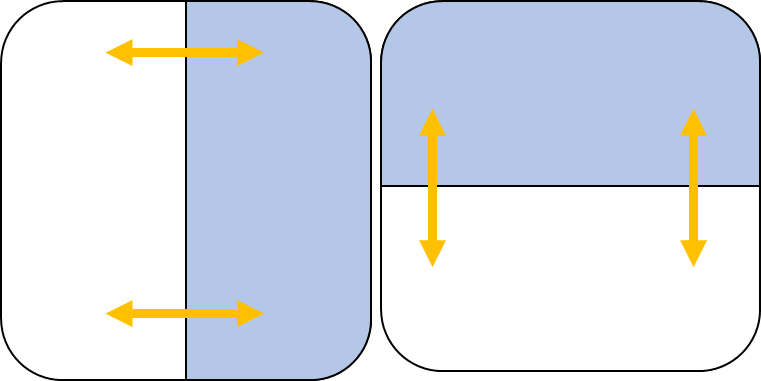
\end{aligned}\tag{7}\] 这里最后的\(\operatorname{upsample}(e_{j}^{l+2})\)是通过原式的\( e_{j}^{l+2} \cdot \frac{\partial p^{l+2}_{j}}{\partial z^{l+1}_{j}} \)得到, 因为原式中\(z_{j}^{l+1}\)到\(p_{j}^{l+2}\)的过程其实是一个下采样池化过程, 而反过来就是上采样, 或者说叫做"反池化" , 反池化操作相比反卷积操作要简单得多, 池化是图像压缩, 那么所谓反池化就是图像扩容, 用一个图就可解释:
虽然本文在1.3节提到了最大池化的优越性, 但是通过图中大家相比也能发现, 在使用最大池化时必须对于选择的最大值位置有所记录, 这样在逆最大值池化时才能将值还原在曾经位置. 这就不如均值池化来得方便. 所以为了方便, 后面我们的代码就默认采用均值池化.(反正本文测试数据小, 也不复杂, 均值池化够用了)
至此, 我们可以得到一个完整的backPropagation的惩罚信息更新图
2.4 backPropagation: 更新边权
刚刚也提到了, 对于BP来说:首先要进行惩罚信息的更新, 其次再完成依据惩罚信息更新边权. 在我的BP那篇博客中, 因为将神经元的阈值\(\theta\)混入到了哑结点中, 因此统一化了边权\(w\). 但是在CNN中再度引入了阈值之后算法需要更新的权有两个, 一个是常规边权, 一个就是偏差, 而常规边权在CNN中是以二维的卷积核出现.
这里没有考虑池化层的非线性激发,因此池化层是不存在可以考虑更新的边权, 我们的目光主要在池化层到卷积层中间的这层卷积核的更新操作, 比方说例图中的\(l+1\)层的卷积核. 试着用损失函数\(E\)对卷积核\(K^{l+1}_{ij}\)求导:\[\begin{aligned}
\bigtriangledown K_{ij}^{l+1} & = \frac{\partial E}{\partial K^{l+1}_{ij}}\\
&= \frac{\partial E}{\partial z^{l+1}_{j}} \cdot \frac{\partial z^{l+1}_{j}}{\partial K^{l+1}_{ij}} = e^{l+1}_{j} \cdot \frac{\partial z^{l+1}_{j}}{\partial K^{l+1}_{ij}} \end{aligned}\] 上式中\(\frac{\partial E}{\partial z^{l+1}_{j}}\)是已知的\(e^{l+1}_{j}\), 但是\(\frac{\partial z^{l+1}_{j}}{\partial K^{l+1}_{ij}}\)是卷积操作的结果Feature Map反过来对卷积核求导的过程, 这个要怎么算呢?
为了方便考虑, 我们把数据稍微降维, 把目光投入到一个3阶矩阵与2阶卷积核求卷积的过程.首先正向考虑, forward时这层一定存在卷积操作\[p^{l} * K^{l+1} = z^{l+1}\] 列出\(p,K,z\)矩阵的表达式如下(为方便我把上标也忽略了)\[\left(\begin{array}{lll}
p_{11} & p_{12} & p_{13} \\
p_{21} & p_{22} & p_{23} \\
p_{31} & p_{32} & p_{33}
\end{array}\right) *\left(\begin{array}{ll}
k_{11} & k_{12} \\
k_{21} & k_{22}
\end{array}\right)=\left(\begin{array}{cc}
z_{11} & z_{12} \\
z_{21} & z_{22}
\end{array}\right)\] 利用卷积定义, 上面的矩阵式可以分类为四个等式组:\[\left\{\begin{matrix}
z_{11}=p_{11} k_{11}+p_{12} k_{12}+p_{21} k_{21}+p_{22} k_{22} \\
z_{12}=p_{12} k_{11}+p_{13} k_{12}+p_{22} k_{21}+p_{23} k_{22} \\
z_{21}=p_{21} k_{11}+p_{22} k_{12}+p_{31} k_{21}+p_{32} k_{22} \\
z_{22}=p_{22} k_{11}+p_{23} k_{12}+p_{32} k_{21}+p_{33} k_{22}
\end{matrix}\right.\] 有了这个等式组之后我们就可以将\(\frac{\partial z^{l+1}_{j}}{\partial K^{l+1}_{ij}}\)的求导计算给降维, 并且从不熟悉的卷积偏导转变为熟悉的多个等式的求偏导, 分别计算\(\frac{\partial z}{\partial k_{uv}}(1 \le u,v \le 2)\)有: \[\left\{\begin{matrix}
\frac{\partial z}{\partial k_{uv}} = \sum^{2}_{i=1}\sum^{2}_{j=1}\frac{\partial z_{ij}}{\partial k_{uv}}\\
\frac{\partial z}{\partial k_{11}}=p_{11} +p_{12}+p_{21}+p_{22} \\
\frac{\partial z}{\partial k_{12}}=p_{12} +p_{13}+p_{22}+p_{23} \\
\frac{\partial z}{\partial k_{21}}=p_{21} +p_{22}+p_{31}+p_{32} \\
\frac{\partial z}{\partial k_{22}}=p_{22} +p_{23}+p_{32}+p_{33}
\end{matrix}\right.\] 这个过程是如何取得的呢, 举个例子大家就明白了, 例如计算\(\frac{\partial z}{\partial k_{21}}\), 这个算式可以通过\(z\)的角度进行展开:\(\frac{\partial z}{\partial k_{21}} = \frac{\partial z_{11}}{\partial k_{21}}+\frac{\partial z_{12}}{\partial k_{21}}+\frac{\partial z_{21}}{\partial k_{21}}+\frac{\partial z_{22}}{\partial k_{21}}\), 而这四个值刚好对应刚刚的四个等式组第三列的系数.
明白这步之后 , 让我们更进一步思考一下\(e^{l+1}\)的特征(这个\(e\)我把下标\(j\)删去了, 因为目前我们并不考虑多个平面切片的问题, 而是单纯地对于一个矩阵的思考), 它是来自backPropagation过程中得到的惩罚信息构成的矩阵, 上面文字也提到过了, 惩罚信息矩阵尺寸大小与本层切片尺寸是一致. 因此在我们当前的假设里, \(e^{l+1}\)应该是一个2*2的矩阵, 大小和\(z^{l+1}\)一样. ok, 现在我再重新看看我们刚刚推导到一半的公式(将原有网络的下标特征删去后)\( \bigtriangledown K^{l+1} = \frac{\partial E}{\partial K^{l+1}} = e^{l+1} \cdot \frac{\partial z^{l+1}}{\partial K^{l+1}} \) 这个公式的惩罚误差\(e\)部分是由\(e_{11},e_{12},e_{21},e_{22}\)这四个标量构成的2*2矩阵, 而最终计算得到的\(\bigtriangledown K^{l+1}\)显然也是一个矩阵形式, 于是可将\(\bigtriangledown K^{l+1}\)的公式表示扩展到标量化的表示(即\(\bigtriangledown K^{l+1}_{uv} = \frac{\partial E}{\partial K^{l+1}_{uv}} = e^{l+1}_{uv} \cdot \frac{\partial z^{l+1}}{\partial K^{l+1}_{uv}}\), 注意, 这个公式中的所有包含uv的都是一个标量值), 这样\(e\)本身的标量就能和同样可以分解为标量的\(\frac{\partial z^{l+1}}{\partial K^{l+1}}\)建立乘法关系, 最终得到下面的结论:\[\left\{\begin{matrix}
\frac{\partial E}{\partial K_{11}^{l+1}}=p_{11}e_{11} + p_{12}e_{12} +p_{21}e_{21} + p_{22}e_{22}\\
\frac{\partial E}{\partial K_{12}^{l+1}}=p_{12} e_{11}+p_{13} e_{12}+p_{22} e_{21}+p_{23} e_{22} \\
\frac{\partial E}{\partial K_{13}^{l+1}}=p_{13} e_{11}+a_{14} e_{12}+a_{23} e_{21}+a_{24} e_{22} \\
\frac{\partial E}{\partial K_{21}^{l+1}}=p_{21} e_{11}+p_{22} e_{12}+p_{31} e_{21}+p_{32} e_{22} \\
\dots
\end{matrix}\right.\] 这个式子转化为矩阵表示就是:\[\frac{\partial E}{\partial K^{l+1}}=\left(\begin{array}{llll}
p_{11} & p_{12} & p_{13}\\
p_{21} & p_{22} & p_{23}\\
p_{31} & p_{32} & p_{33}
\end{array}\right) *\left(\begin{array}{cc}
e_{11} & e_{12} \\
e_{21} & e_{22}
\end{array}\right)\] 终于! 我们成功推导出了边权更新的梯度表示, 用这个方法来处理卷积求导将会非常有用!! 如果把上面的\(z^{l+1}\)向\(K^{l+1}\)求偏导替换为向\(p^{l}\)求偏导, 那么就变回了求\(l\)层惩罚因子的问题, 这个时候再套用上面的方案你就会得到旋转了180度的卷积核\(K\), 这也就是公式5的来源.
最终附上旧式与梯度步长\(\alpha\)有公式, 我们给出CNN中卷积核边权的更新公式:\[\bigtriangledown K^{l+1}_{ij} = p^{l}_{i}* e^{l+1}_{j} \tag{8} \] \[K^{l+1}_{ij} = \lambda K^{l+1}_{ij} + \alpha \bigtriangledown K^{l+1}_{ij} \tag{9} \] 这里\(\ \lambda\)用于修饰旧的卷积核的影响.
最后关于偏差\(\mathbf{b}\)的更新就显得格外简单粗暴了.\(\mathbf{b}\)很特殊, 它是这个张量主导的神经网络中唯一的向量, 因此他的处理比较简单, 同时也很灵活. 通常的做法就是将后继结点backPropagation过程中传递过来的惩罚信息矩阵\(e\)中的每个神经元求和就好了. 因此有公式:\[\bigtriangledown b^{l}_{i} = \frac{\partial E}{\partial b^{l}_{i}}=\sum_{u, v}\left(e^{l}_{i}\right)_{u, v} \tag{10}\]\[b^{l}_{i} = b^{l}_{i} + \alpha \bigtriangledown b^{l}_{i} \tag{11} \] 最后, 注意两点, 首先偏差值是激活函数的参数, 因此这个值是卷积层特有的, 池化层不具备; 第二, 有时候我们分batch学习的时候, 还习惯把几个batch得到的平行的惩罚信息求和再取平均, 我们代码正是采用这个思路.
3. 卷积的神经网络代码实现总思路梳理
本文的代码并没有采用库, 因此我们大概需要对于需要实现的工作进行一个计划和相关库的封装准备.
我们使用数据集是train,format, 可以在此处 https://github.com/FanSmale/sampledata/ , 这个数据集中有12001个数据行, 每个数据行都由784个0/1外加一个标签值构成, 784个0/1其实是表征一个28*28的手写体矩阵的像素平铺之后的结构, 而标签值是一个位于0~9的数组, 用来表示此平铺像素还原到二维图像后所写下的字体.
我们需要设计一个针对如此结构的良好数据结构以及作用于此结构上的一组操作来方便后续代码的工作. 当然可以使用weka库, 但是本文采用的是自构建的类Dataset来完成的, Dataset是一个组合类, 其由自构建的行数据类Instance通过util.List的线性结构组合而成. 这个行数据就是用于存储784+1的pixel与label的单行数据.
有了库之后需要定义CNN需要的一些组件, 首先定义一个Size类来完成基本的二维图像的简单属性与运算, 比如我们在卷积中频繁用到了矩阵尺度转换. 然后基于Size类的方法, 进一步形成MathUtils类, 这个类将是我们CNN代码的工具箱, 我们所有的卷积(Valid与Full两个模式)操作与池化和反池化操作的代码都将在这里定义, 同时这个库还定义了矩阵的基本加和运算以及运算符接口(运算符接口可以极大简化单/双操作数的运算, 避免重复操作, 提高重用性)
CnnLayer类是单纯地定义CNN层的单层框架体系的, 在实际训练中我们总是要先定义完善一个单层框架, 然后通过CnnBuilder类将这个框架体系串联起来构成完整的CNN全局框架. 这里将会根据自定义枚举LayerTypeEnum来区分这些每层的框架.
FullCnn类是依据CnnBuilder确立的Cnn框架为基础, 再结合MathUtils的内核进行训练的核心类. 在这个类中我们将完成四件大事:
- forward 预测
- backPropagation 设置惩罚信息
- 更新卷积核与偏差值
- 训练的迭代
4. 底层代码: Dataset类与Size类
4.1 Dataset类
首先完成Dataset类中用于存储每一行数据的Instance类, 这个类是Dataset的内嵌类
/**
***********************
* An instance.
***********************
*/
public class Instance {
/**
* Conditional attributes.
*/
private double[] attributes;
/**
* Label.
*/
private Double label;
/**
***********************
* The first constructor.
***********************
*/
private Instance(double[] paraAttrs, Double paraLabel) {
attributes = paraAttrs;
label = paraLabel;
}//Of the first constructor
/**
***********************
* The second constructor.
***********************
*/
public Instance(double[] paraData) {
if (labelIndex == -1)
// No label
attributes = paraData;
else {
label = paraData[labelIndex];
attributes = Arrays.copyOfRange(paraData, 0, labelIndex);
if (labelIndex == paraData.length - 1) {
return;
} // Of if
double[] tempDoubles = Arrays.copyOfRange(paraData, labelIndex + 1, paraData.length);
double[] mergeDoubles = new double[paraData.length - 1];
System.arraycopy(attributes, 0, mergeDoubles, 0, attributes.length);
System.arraycopy(tempDoubles, 0, mergeDoubles, attributes.length, tempDoubles.length);
attributes = mergeDoubles;
} // Of if
}// Of the second constructor
/**
***********************
* Getter.
***********************
*/
public double[] getAttributes() {
return attributes;
}// Of getAttributes
/**
***********************
* Getter.
***********************
*/
public Double getLabel() {
if (labelIndex == -1)
return null;
return label;
}// Of getLabel
/**
***********************
* toString.
***********************
*/
public String toString(){
return Arrays.toString(attributes) + ", " + label;
}//Of toString
}// Of class Instance这里以防万一, 使用Double型作为数据接收的结构, attributes[] 表示图像像素平铺部分, label表示读取的标签值. 另外, 此类是Dataset的内嵌类, 构造函数中直接使用的labelIndex变量表示外层数据集声明的标签所在列, 若未指明(-1), 那么默认无标签; 否则这里用到了Java中的一个拷贝切片函数Arrays.copyOfRange, 分别拷贝了标签前后的数组, 然后利用笨办法System.arraycopy将其俩者合并. 当然本文种标签在最后的数据来说, 后面合并的代码并不会执行.
public class Dataset {
/**
* All instances organized by a list.
*/
private List instances;
/**
* The label index.
*/
private int labelIndex;
/**
***********************
* The first constructor.
***********************
*/
public Dataset() {
labelIndex = -1;
instances = new ArrayList();
}// Of the first constructor
/**
***********************
* The second constructor.
*
* @param paraFilename The filename.
* @param paraSplitSign Often comma.
* @param paraLabelIndex Often the last column.
***********************
*/
public Dataset(String paraFilename, String paraSplitSign, int paraLabelIndex) {
instances = new ArrayList();
labelIndex = paraLabelIndex;
File tempFile = new File(paraFilename);
try {
BufferedReader tempReader = new BufferedReader(new FileReader(tempFile));
String tempLine;
while ((tempLine = tempReader.readLine()) != null) {
String[] tempDatum = tempLine.split(paraSplitSign);
if (tempDatum.length == 0) {
continue;
} // Of if
double[] tempData = new double[tempDatum.length];
for (int i = 0; i < tempDatum.length; i++)
tempData[i] = Double.parseDouble(tempDatum[i]);
Instance tempInstance = new Instance(tempData);
append(tempInstance);
} // Of while
tempReader.close();
} catch (IOException e) {
e.printStackTrace();
System.out.println("Unable to load " + paraFilename);
System.exit(0);
} // Of try
}// Of the second constructor
/**
***********************
* Append an instance.
*
* @param paraInstance The given record.
***********************
*/
public void append(Instance paraInstance) {
instances.add(paraInstance);
}// Of append
/**
***********************
* Append an instance specified by double values.
***********************
*/
public void append(double[] paraAttributes, Double paraLabel) {
instances.add(new Instance(paraAttributes, paraLabel));
}// Of append
/**
***********************
* Getter.
***********************
*/
public Instance getInstance(int paraIndex) {
return instances.get(paraIndex);
}// Of getInstance
/**
***********************
* Getter.
***********************
*/
public int size() {
return instances.size();
}// Of size
/**
***********************
* Getter.
***********************
*/
public double[] getAttributes(int paraIndex) {
return instances.get(paraIndex).getAttributes();
}// Of getAttrs
/**
***********************
* Getter.
***********************
*/
public Double getLabel(int paraIndex) {
return instances.get(paraIndex).getLabel();
}// Of getLabel
/**
***********************
* An instance.
***********************
*/
public class Instance {
// ...
}// Of class Instance
}// Of class Dataset Dataset数据集是通过Instance行数据为基础, 通过List
- append( ) 添加数据行方法, 可以分别调入Double[ ]数组 与 Double标签值; 也可以直接调入Instance对象.
- getInstance( ) 按照行号返回Instance对象
- size( ) 获取行数
- getLabel( ) 按照行号返回对应数据行的标签
- getAttributes( ) 按照行号返回对应数据行的条件属性
4.2 Size类
Size类本质上就是提供了一个二元组与两种方法来表征矩阵核: 包括卷积核与池化的比例核
public class Size {
/**
* Cannot be changed after initialization.
*/
public final int width;
/**
* Cannot be changed after initialization.
*/
public final int height;
/**
***********************
* The first constructor.
*
* @param paraWidth
* The given width.
* @param paraHeight
* The given height.
***********************
*/
public Size(int paraWidth, int paraHeight) {
width = paraWidth;
height = paraHeight;
}// Of the first constructor
/**
***********************
* Divide a scale with another one. For example (4, 12) / (2, 3) = (2, 4).
*
* @param paraScaleSize
* The given scale size.
* @return The new size.
***********************
*/
public Size divide(Size paraScaleSize) {
int resultWidth = width / paraScaleSize.width;
int resultHeight = height / paraScaleSize.height;
if (resultWidth * paraScaleSize.width != width
|| resultHeight * paraScaleSize.height != height)
throw new RuntimeException("Unable to divide " + this + " with " + paraScaleSize);
return new Size(resultWidth, resultHeight);
}// Of divide
/**
***********************
* Subtract a scale with another one, and add a value. For example (4, 12) -
* (2, 3) + 1 = (3, 10).
*
* @param paraScaleSize
* The given scale size.
* @param paraAppend
* The appended size to both dimensions.
* @return The new size.
***********************
*/
public Size subtract(Size paraScaleSize, int paraAppend) {
int resultWidth = width - paraScaleSize.width + paraAppend;
int resultHeight = height - paraScaleSize.height + paraAppend;
return new Size(resultWidth, resultHeight);
}// Of subtract
/**
***********************
* @param The
* string showing itself.
***********************
*/
public String toString() {
String resultString = "(" + width + ", " + height + ")";
return resultString;
}// Of toString
}// Of class Sizedivide( )方法就是针对池化做出的矩阵分割操作, 按照比例核的大小到当前this对象中去"圈地", 圈出的部分全部组合为新的矩阵返回; subtract的话就是套用公式1计算按照卷积核大小去执行卷积操作后Feature Map的尺寸大小, 本代码因为是针对已知CNN结构来编写的, 所以关于卷积操作尺寸计算中stride与zero-padding值都是默认为1与0的, 其实规范点的话这几个值应当作为参数传入, 是可调的.
5. 关键的运算代码: Operator接口 与 MathUtils类
* Operator接口
Java中提供一种名为interface的特殊结构, 我们称之为接口(inferface), 接口是抽象类的衍生, 接口中所有方法均无方法体, 只提供了单纯的方法名称, 等待调用时去实现.
/**
* An interface for different on-demand operators.
*/
public interface Operator extends Serializable {
public double process(double value);
}// Of interfact Operator
/**
* An interface for operations with two operators.
*/
interface OperatorOnTwo extends Serializable {
public double process(double a, double b);
}// Of interface OperatorOnTwo上述代码定义了两个接口, 每个接口只掌管了一个未实现的函数接口process. 虽然这两个函数同名, 但是分别定义与不同接口中因此具有不同特性. 逻辑上, 计划将前者用于实现但操作数操作, 后者用于实现多操作数操作.
拓展:
继承的Serializable类是一个空接口,没有什么具体内容,它的目的只是简单的标识一个类的对象可以被序列化
/**
* The one-minus-the-value operator.
*/
public static final Operator one_value = new Operator() {
private static final long serialVersionUID = 3752139491940330714L;
@Override
public double process(double value) {
return 1 - value;
}// Of process
};
/**
* Plus.
*/
public static final OperatorOnTwo plus = new OperatorOnTwo() {
private static final long serialVersionUID = -6298144029766839945L;
@Override
public double process(double a, double b) {
return a + b;
}// Of process
};
/**
* Multiply.
*/
public static OperatorOnTwo multiply = new OperatorOnTwo() {
private static final long serialVersionUID = -7053767821858820698L;
@Override
public double process(double a, double b) {
return a * b;
}// Of process
};
/**
* Minus.
*/
public static OperatorOnTwo minus = new OperatorOnTwo() {
private static final long serialVersionUID = 7346065545555093912L;
@Override
public double process(double a, double b) {
return a - b;
}// Of process
};这里展示了实现接口方法具体手段, 创建一个接口对象并且用new声明空间并且赋初值时重写接口内的方法. 之后这个函数对象就指向了重写的方法, 后续在调用到这个函数地址时能直接使用当前的重写方法. 上述完成了一些基本运算的说明, 注意, one_value接口对象对应的1 - A算子其实是Sigmoid求导后一部分, 这里预写出来, 到时候直接可以作为单操作数运算符调用.
* 矩阵逆置180°
/**
***********************
* Rotate the matrix 180 degrees.
***********************
*/
public static double[][] rot180(double[][] matrix) {
matrix = cloneMatrix(matrix);
int m = matrix.length;
int n = matrix[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n / 2; j++) {
double tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - 1 - j];
matrix[i][n - 1 - j] = tmp;
}
}
for (int j = 0; j < n; j++) {
for (int i = 0; i < m / 2; i++) {
double tmp = matrix[i][j];
matrix[i][j] = matrix[m - 1 - i][j];
matrix[m - 1 - i][j] = tmp;
}
}
return matrix;
}// Of rot180rot180( )是反池化传播的时候需要进行的运算一部分, 这里需要将矩阵翻转180度. 这里运用了一维翻转到二维的技巧, 一维的翻转想必都知道, 其实二维的翻转本身就结果来说, 也会导致原矩阵的左右逆置, 上下逆置, 其实就是一维在两个方向的体现. 因此代码中, 我们将矩阵进行两次操作, 第一次实现全局左右数据交换, 第二次实现全局上下交换就好了.
* 随机值初始化矩阵
private static Random myRandom = new Random(2);
/**
***********************
* Generate a random matrix with the given size. Each value takes value in
* [-0.005, 0.095].
***********************
*/
public static double[][] randomMatrix(int x, int y) {
double[][] matrix = new double[x][y];
// int tag = 1;
for (int i = 0; i < x; i++) {
for (int j = 0; j < y; j++) {
matrix[i][j] = (myRandom.nextDouble() - 0.05) / 10;
} // Of for j
} // Of for i
return matrix;
}// Of randomMatrix
/**
***********************
* Generate a random array with the given length. Each value takes value in
* [-0.005, 0.095].
***********************
*/
public static double[] randomArray(int len) {
double[] data = new double[len];
for (int i = 0; i < len; i++) {
data[i] = myRandom.nextDouble() / 10 - 0.05;
} // Of for i
return data;
}// Of randomArray
/**
***********************
* Generate a random perm with the batch size.
***********************
*/
public static int[] randomPerm(int size, int batchSize) {
Set set = new HashSet();
while (set.size() < batchSize) {
set.add(myRandom.nextInt(size));
}
int[] randPerm = new int[batchSize];
int i = 0;
for (Integer value : set)
randPerm[i++] = value;
return randPerm;
}// Of randomPerm 虽然说神经网络的边权初始化有许多更有适用性与效率的初始化技巧, 但是对于CNN的基本模拟来说, 随机值初始化也不失一个简单且快捷的好办法.
- double[][] randomMatrix(int x, int y) 生成一个x*y的矩阵, 矩阵内每个值是范围位于[-0.005, 0.095) 这里有意控制大小是为了避免Sigmoid出现梯度爆炸
- double[] randomArray(int len) 生成长度为len的随机值矩阵, 单个值范围依旧是[-0.005, 0.095)
- int[] randomPerm(int size, int batchSize) 在[0,size)的范围内随机生成batchSize个不重叠的值, 这个方法将会用到batch训练中. 代码中, 我们使用了Java的集合方法Set来回避区域重复.
* 矩阵基础运算1
/**
***********************
* Clone a matrix. Do not use it reference directly.
***********************
*/
public static double[][] cloneMatrix(final double[][] matrix) {
final int m = matrix.length;
int n = matrix[0].length;
final double[][] outMatrix = new double[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
outMatrix[i][j] = matrix[i][j];
} // Of for j
} // Of for i
return outMatrix;
}// Of cloneMatrix
/**
***********************
* Matrix operation with the given operator on single operand.
***********************
*/
public static double[][] matrixOp(final double[][] ma, Operator operator) {
final int m = ma.length;
int n = ma[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
ma[i][j] = operator.process(ma[i][j]);
} // Of for j
} // Of for i
return ma;
}// Of matrixOp
/**
***********************
* Matrix operation with the given operator on two operands.
***********************
*/
public static double[][] matrixOp(final double[][] ma, final double[][] mb,
final Operator operatorA, final Operator operatorB, OperatorOnTwo operator) {
final int m = ma.length;
int n = ma[0].length;
if (m != mb.length || n != mb[0].length)
throw new RuntimeException("ma.length:" + ma.length + " mb.length:" + mb.length);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
double a = ma[i][j];
if (operatorA != null)
a = operatorA.process(a);
double b = mb[i][j];
if (operatorB != null)
b = operatorB.process(b);
mb[i][j] = operator.process(a, b);
} // Of for j
} // Of for i
return mb;
}// Of matrixOpCNN中免不了一些简单的矩阵基础运算, 我们已经在最开始的Size类中实现了两个会用得上了运算核的运算, 现在进一步完成矩阵的运算推广. 本文描述的CNN中出现的矩阵运算都还是比较简单的同阶运算, 这里就体现我们提前建立统一的运算符接口的明智之处了, 采用了统一的接口之后, 我们可以加强矩阵运算函数的重用性, 避免一个运算写个matrixOp的极大冗余.
- double[][] cloneMatrix(final double[][] matrix) 顾名思义 , 矩阵拷贝
- double[][] matrixOp(final double[][] ma, Operator operator) 矩阵的单操作数运算, operator为定义的Operator接口的对象, 其值决定了矩阵的运算
- double[][] matrixOp(final double[][] ma, final double[][] mb,
final Operator operatorA, final Operator operatorB, OperatorOnTwo operator) 矩阵的双操作数运算, 双操作树运算中加入了对于运算算法各种可能还会采用单运算的考虑(比如ax+cy这种情况) 因此在双运算Operator接口对象operator的前提下还额外增加了两个单运算Operator接口对象operatorA 与 operatorB.
* 矩阵基础运算2
/**
***********************
* Sum all values of a matrix.
***********************
*/
public static double sum(double[][] error) {
int m = error.length;
int n = error[0].length;
double sum = 0.0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sum += error[i][j];
}
}
return sum;
}// Of sum
/**
***********************
* Ad hoc sum.
***********************
*/
public static double[][] sum(double[][][][] errors, int j) {
int m = errors[0][j].length;
int n = errors[0][j][0].length;
double[][] result = new double[m][n];
for (int mi = 0; mi < m; mi++) {
for (int nj = 0; nj < n; nj++) {
double sum = 0;
for (int i = 0; i < errors.length; i++)
sum += errors[i][j][mi][nj];
result[mi][nj] = sum;
}
}
return result;
}// Of sum
/**
***********************
* Get the index of the maximal value for the final classification.
***********************
*/
public static int getMaxIndex(double[] out) {
double max = out[0];
int index = 0;
for (int i = 1; i < out.length; i++)
if (out[i] > max) {
max = out[i];
index = i;
}
return index;
}// Of getMaxIndex此外在计算偏差的更新时, 可能会计算多个平行batch的神经网络中的错误矩阵的数据和, 因此专门准备了两个求和的sum函数. 这里有个参数double[][][][] errors我们会在后面解释, 简单来说, 这个sum的目的是将这个数组最后两维构成的二维平面内的数据求和得到一个\(x\), 然后固定住第二维, 再将所有一维展开的errors结构中的\(x\)全部加起来. 这个解释起来可能有点抽象, 具体我将在后续的updateBias函数中解释这个问题.
- double sum(double[][] error) 惩罚信息矩阵每个元素求和, 并返回求和值
- double sum(double[][][][] errors, int j) 固定第二维为j, 然后进行全维求和, 并返回求和值
- int getMaxIndex(double[] out) 返回out数组最大下标
* 两种卷积
/**
***********************
* Convolution operation, from a given matrix and a kernel, sliding and sum
* to obtain the result matrix. It is used in forward.
***********************
*/
public static double[][] convnValid(final double[][] matrix, double[][] kernel) {
// kernel = rot180(kernel);
int m = matrix.length;
int n = matrix[0].length;
final int km = kernel.length;
final int kn = kernel[0].length;
int kns = n - kn + 1;
final int kms = m - km + 1;
final double[][] outMatrix = new double[kms][kns];
for (int i = 0; i < kms; i++) {
for (int j = 0; j < kns; j++) {
double sum = 0.0;
for (int ki = 0; ki < km; ki++) {
for (int kj = 0; kj < kn; kj++)
sum += matrix[i + ki][j + kj] * kernel[ki][kj];
}
outMatrix[i][j] = sum;
}
}
return outMatrix;
}// Of convnValid
/**
***********************
* Convolution full to obtain a bigger size. It is used in back-propagation.
***********************
*/
public static double[][] convnFull(double[][] matrix, final double[][] kernel) {
int m = matrix.length;
int n = matrix[0].length;
final int km = kernel.length;
final int kn = kernel[0].length;
final double[][] extendMatrix = new double[m + 2 * (km - 1)][n + 2 * (kn - 1)];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
extendMatrix[i + km - 1][j + kn - 1] = matrix[i][j];
} // Of for j
} // Of for i
return convnValid(extendMatrix, kernel);
}// Of convnFull两种卷积操作分别对应着Valid模式的基本卷积操作与扩展版的Full卷积, Valid模式是常规尺寸会减少的卷积, 详细的操作可见1.3节, 理解之后代码反而很简单. Full卷积本质上就是对于被卷积的矩阵外层套上一层宽度是卷积核的" 宽度-1 "的" 0 "外壳然后再进行卷积操作, 想起推导与证明可见2.3.2节. 所以说其实convFull只需要完成" 套边 "这个操作, 然后无脑调用convnValid即可.
- double[][] convnValid(final double[][] matrix, double[][] kernel) Valid模式卷积(常规的卷积操作), 用于forward正向传递的值预测.
- double[][] convnFull(double[][] matrix, final double[][] kernel) Full模式卷积, 用于backPropagation逆向传递的惩罚信息更新, 是池化层反向传播更新惩罚信息的关键卷积操作.
* 池化与反池化
/**
***********************
* Scale the matrix.
***********************
*/
public static double[][] scaleMatrix(final double[][] matrix, final Size scale) {
int m = matrix.length;
int n = matrix[0].length;
final int sm = m / scale.width;
final int sn = n / scale.height;
final double[][] outMatrix = new double[sm][sn];
if (sm * scale.width != m || sn * scale.height != n)
throw new RuntimeException("scale matrix");
final int size = scale.width * scale.height;
for (int i = 0; i < sm; i++) {
for (int j = 0; j < sn; j++) {
double sum = 0.0;
for (int si = i * scale.width; si < (i + 1) * scale.width; si++) {
for (int sj = j * scale.height; sj < (j + 1) * scale.height; sj++) {
sum += matrix[si][sj];
} // Of for sj
} // Of for si
outMatrix[i][j] = sum / size;
} // Of for j
} // Of for i
return outMatrix;
}// Of scaleMatrix
/**
***********************
* Extend the matrix to a bigger one (a number of times).
***********************
*/
public static double[][] kronecker(final double[][] matrix, final Size scale) {
final int m = matrix.length;
int n = matrix[0].length;
final double[][] outMatrix = new double[m * scale.width][n * scale.height];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int ki = i * scale.width; ki < (i + 1) * scale.width; ki++) {
for (int kj = j * scale.height; kj < (j + 1) * scale.height; kj++) {
outMatrix[ki][kj] = matrix[i][j];
}
}
}
}
return outMatrix;
}// Of kronecker本代码采用的池化是均值池化, 上文在介绍反池化时有所提到, 最大池化固然好, 但是反向传播时要记录池化前的数据位置略显麻烦, 因此为了方便采用了均值池化. 具体关于反池化可见2.3.4节
- double[][] scaleMatrix(final double[][] matrix, final Size scale) 均值池化操作, 用于forward正向传播中对于值的预测.
- double[][] kronecker(final double[][] matrix, final Size scale) 均值反池化, 用于backPropagation逆向传播中对于惩罚信息的更新, 是卷积层更新惩罚信息进行上采样的关键函数.
6. CNN框架代码: CnnLayer类与LayerBuilder类
这两个类用于在训练前构建基本的CNN框架体系, 其中解释的一些变量是整个CNN代码的关键, 理解这些变量的含义将会非常有利于对于全局代码的感知.
6.1 CnnLayer类与其成员变量解释
public enum LayerTypeEnum {
INPUT, CONVOLUTION, SAMPLING, OUTPUT;
}//Of enum LayerTypeEnum
/**
* The type of the layer.
*/
LayerTypeEnum type;代码中将层划分为四个类别, 这是个类别将是后面定义代码的关键.
*关于batch训练
这里需要解释下batch训练, 所谓的batch训练就是面对有\(N\)个数据的训练集, 分\(k\)批次地随机地取出\(m\)个随机数据来测试, 因此, 我们最终会给神经网络喂\(km\)个数据. batch中文翻译正是批次的意思. 这种训练有一个特点就是同个批次内的\(m\)次训练获得的结果可以共享成果, 这个方案在神经网络的算法体系中有一个可行的应用就是权值更新的分离, 常规来说神经网络算法在训练一条数据时会在forward预测之后就进行backPropagation计算惩罚信息并更新权值, 我上篇BP算法的文章中就是采用的这种策略, 但是使用了batch训练之后可以略去当前批次中每个数据的权值更新操作, 转而在当前批次结束之后, 利用平行的\(m\)个数据的惩罚信息资料来共同更新惩罚信息.
因此这就塑造我们数据的基本框架, 明白这个之后继续代码解析.
*成员变量解析
/**
* The number of out map.
*/
int outMapNum;
/**
* The map size.
*/
Size mapSize;
/**
* Out maps. Dimensions:
* [batchSize][outMapNum][mapSize.width][mapSize.height].
*/
private double[][][][] outMaps;
/**
* For batch processing.
*/
private static int recordInBatch = 0;这里的变量都是关于forward过程中一层的结构部分, 这里outMaps的四维结构的第一维就是表示当前隶属于当前批次内第几步, 若当前批次容量为batchSize, 那么就表明当前批次由batchSize个数据行构成, 那么这里第一维的大小就是batchSize了. 第二维就表示当前CNN层中切片的个数, 后两维表示单个切片的二维信息.
额外提一句, 为什么叫做outmap呢?, 可以参考2.1节中给出的网络示意图, 本文是默认把" 边 + 边某末端的切片集 "这个整体作为一层的, 所以这些切片特征映射集合是" out "得到的, 故命名为outmap. 此外, 成员变量recordInBatch表示当前的神经网络属于当前批次内的第几个记录号, 这个记录号会在训练时批次内for的执行而更新. 后续还设置了两个函数来实现其初始化与递增:
prepareForNewRecord() -> recordInBatch++
prepareForNewBatch() -> recordInBatch = 0
/**
* Errors.
*/
private double[][][][] errors;批次内的每次记录都需要更新错误信息, 因此错误信息数组errors[][][][]也使用了类似结构, 而且错误信息是对于原CNN的特征映射的更新, 因此层的深度outMapNum与mapSize, errors都是共享的.
/**
* The kernel size.
*/
Size kernelSize;
/**
* The scale size.
*/
Size scaleSize;
/**
* Kernel. Dimensions: [front map][out map][width][height].
*/
private double[][][][] kernel;虽然说边权-卷积核kernel也是一个四维的数组, 但是其含义相比于outmap与errors却有出入. 因为在同一个批次内每次进行记录更新时边权并没有参与更新, 简言之kernel的取值与批次batch没有任何关系. 而kernel作为一个卷积核, 它在CNN中充当的就是一个边权的角色, 因此可以将其视作一种值为矩阵的"边", 所以kernel的前两维分别表示了边的前/后层切片号, 后两维表示卷积核的长宽, 通过前两维可以唯一确定一条边. 至于池化的比例核这里就不专门设置数组了, 泛化地使用kernel表示, 只不过在参与运算时代入scaleSize就好了.
/**
* Bias. The length is outMapNum.
*/
private double[] bias;偏差值用于表征每层切片本身的特征, 因此它没有前层与后层的概念, 只有本层的含义. 而且偏差本身\(b\)本身不是矩阵, 只是一个值. 综上, bias是一维的向量, 注意这个不同于kernel的特点.
*构造函数与初始化
/**
***********************
* The first constructor.
*
* @param paraNum
* When the type is CONVOLUTION, it is the out map number. when
* the type is OUTPUT, it is the class number.
* @param paraSize
* When the type is INPUT, it is the map size; when the type is
* CONVOLUTION, it is the kernel size; when the type is SAMPLING,
* it is the scale size.
***********************
*/
public CnnLayer(LayerTypeEnum paraType, int paraNum, Size paraSize) {
type = paraType;
switch (type) {
case INPUT:
outMapNum = 1;
mapSize = paraSize; // No deep copy.
break;
case CONVOLUTION:
outMapNum = paraNum;
kernelSize = paraSize;
break;
case SAMPLING:
scaleSize = paraSize;
break;
case OUTPUT:
outMapNum = paraNum;
mapSize = new Size(1, 1);
break;
default:
System.out.println("Internal error occurred in AbstractLayer.java constructor.");
}// Of switch
}// Of the first constructor从构造函数中我们能一瞥每层的特点:
| Input Layer | Convolution Layer | Sampling Layer | Output Layer | |
| outputMapNum | 1 | paraNum | / | paraNum |
| mapSize | paraSize | paraSize | paraSize | Size(1, 1) |
有些层的值初始不由外界带入参数确定而是又CNN本身架构确定, 例如输出层的切片大小是1*1, 这是由我们这个无flatten化和全连接部件的CNN确定的. 池化层不用初始层深度是因为它的深度与它前面的卷积层是共享深度的.
/**
***********************
* Initialize the kernel.
*
* @param paraNum
* When the type is CONVOLUTION, it is the out map number. when
***********************
*/
public void initKernel(int paraFrontMapNum) {
kernel = new double[paraFrontMapNum][outMapNum][][];
for (int i = 0; i < paraFrontMapNum; i++) {
for (int j = 0; j < outMapNum; j++) {
kernel[i][j] = MathUtils.randomMatrix(kernelSize.width, kernelSize.height);
} // Of for j
} // Of for i
}// Of initKernel
/**
***********************
* Initialize the output kernel. The code is revised to invoke
* initKernel(int).
***********************
*/
public void initOutputKernel(int paraFrontMapNum, Size paraSize) {
kernelSize = paraSize;
initKernel(paraFrontMapNum);
}// Of initOutputKernel
/**
***********************
* Initialize the bias. No parameter. "int frontMapNum" is claimed however
* not used.
***********************
*/
public void initBias() {
bias = MathUtils.randomArray(outMapNum);
}// Of initBias
/**
***********************
* Initialize the errors.
*
* @param paraBatchSize
* The batch size.
***********************
*/
public void initErrors(int paraBatchSize) {
errors = new double[paraBatchSize][outMapNum][mapSize.width][mapSize.height];
}// Of initErrors
/**
***********************
* Initialize out maps.
*
* @param paraBatchSize
* The batch size.
***********************
*/
public void initOutMaps(int paraBatchSize) {
outMaps = new double[paraBatchSize][outMapNum][mapSize.width][mapSize.height];
}// Of initOutMaps输出层其实也是一种卷积层, 不同的地方只是在于一般的卷积层的卷积尺寸是可以自定义的, 但是输出层的卷积尺寸必须要与输出层本身的Feature Map尺寸一致以保证能输出1*1的矩阵. 所以在输出层的kernel初始化中我们将kernel的尺寸调整得与mapSize一致并调用了卷积层的初始化函数. 同时在这些与批次内记录数相关的四维数组进行初始化时可能需要按照情况初始化批次内的记录数, 但是前提是此时当前层的切片数要提前确立.
*一些setter和getter
public void setMapValue(int paraMapNo, int paraX, int paraY, double paraValue) {
outMaps[recordInBatch][paraMapNo][paraX][paraY] = paraValue;
}// Of setMapValue
public void setMapValue(int paraMapNo, double[][] paraOutMatrix) {
outMaps[recordInBatch][paraMapNo] = paraOutMatrix;
}// Of setMapValue
public double[][] getMap(int paraIndex) {
return outMaps[recordInBatch][paraIndex];
}// Of getMap
public double[][] getKernel(int paraFrontMap, int paraOutMap) {
return kernel[paraFrontMap][paraOutMap];
}// Of getKernel
public void setError(int paraMapNo, int paraMapX, int paraMapY, double paraValue) {
errors[recordInBatch][paraMapNo][paraMapX][paraMapY] = paraValue;
}// Of setError
public void setError(int paraMapNo, double[][] paraMatrix) {
errors[recordInBatch][paraMapNo] = paraMatrix;
}// Of setError
public double[][] getError(int paraMapNo) {
return errors[recordInBatch][paraMapNo];
}// Of getError
public double[][] getError(int paraRecordId, int paraMapNo) {
return errors[paraRecordId][paraMapNo];
}// Of getError
public void setKernel(int paraLastMapNo, int paraMapNo, double[][] paraKernel) {
kernel[paraLastMapNo][paraMapNo] = paraKernel;
}// Of setKernel
public double getBias(int paraMapNo) {
return bias[paraMapNo];
}// Of getBias
public void setBias(int paraMapNo, double paraValue) {
bias[paraMapNo] = paraValue;
}// Of setBias
public double[][] getMap(int paraRecordId, int paraMapNo) {
return outMaps[paraRecordId][paraMapNo];
}// Of getMap这里我删去了不会被使用和见名称就知道的setter与getter(并且把函数说明删去了), 主要列出了一些要特殊强强调的部分.
- void setMapValue(int paraMapNo, int paraX, int paraY, double paraValue) 把数值paraValue赋值给当前层的第paraMapNo个切片的(paraX, paraY)位置. (本层所在的神经网络所属的批次内记录号recordInBatch隐含于当前CnnLayer类内部)
- void setMapValue(int paraMapNo, double[][] paraOutMatrix) 把矩阵paraOutMatrix赋值给当前层的第paraMapNo个切片. (本层所在的神经网络所属的批次内记录号recordInBatch隐含于当前CnnLayer类内部)
- double[][] getMap(int paraIndex) 获取当前层的第paraMapNo个切片矩阵本身. 本层所在的神经网络所属的批次内记录号recordInBatch隐含于当前CnnLayer类内部.
- double[][] getMap(int paraRecordId, int paraMapNo) 获得批次内第paraRecordId个CNN神经网络中的当前层的第paraMapNo个切片矩阵.
- void setError(int paraMapNo, int paraMapX, int paraMapY, double paraValue) 把数值paraValue赋值给当前层的第paraMapNo个惩罚信息矩阵的(paraMapX, paraMapY)位置. (本层所在的神经网络所属的批次内记录号recordInBatch隐含于当前CnnLayer类内部)
- void setError(int paraMapNo, double[][] paraMatrix) 把矩阵paraMatrix给当前层的第paraMapNo个惩罚信息矩阵本身.(本层所在的神经网络所属的批次内记录号recordInBatch隐含于当前CnnLayer类内部)
- double[][] getError(int paraMapNo) 获得当前层的第paraMapNo个惩罚信息矩阵 (本层所在的神经网络所属的批次内记录号recordInBatch隐含于当前CnnLayer类内部)
- double[][] getError(int paraRecordId, int paraMapNo) 获得批次内第paraRecordID个CNN神经网络中的当前层的第paraMapNo个惩罚信息矩阵.
- void setKernel(int paraLastMapNo, int paraMapNo, double[][] paraKernel) 设置前层paraLastMapNo切片与后层paraMapNo切片之间的卷积核矩阵paraKernel.
- double[][] getKernel(int paraFrontMap, int paraOutMap) 获取前层paraFrontMap切片与后层paraOutMap切片之间的卷积核矩阵.
- double getBias(int paraMapNo). 获取本层的第paraFrontMap个偏差.
- void setBias(int paraMapNo, double paraValue). 设置本层的第paraFrontMap个偏差值为paraValue.
6.2 LayerBuilder类
CnnLayer类成功确立后, LayerBuilder就很简单了, 它只是将CnnLayer数组化的类而已.
public class LayerBuilder {
/**
* Layers.
*/
private List layers;
/**
***********************
* The first constructor.
***********************
*/
public LayerBuilder() {
layers = new ArrayList();
}// Of the first constructor
/**
***********************
* The second constructor.
***********************
*/
public LayerBuilder(CnnLayer paraLayer) {
this();
layers.add(paraLayer);
}// Of the second constructor
/**
***********************
* Add a layer.
*
* @param paraLayer
* The new layer.
***********************
*/
public void addLayer(CnnLayer paraLayer) {
layers.add(paraLayer);
}// Of addLayer
/**
***********************
* Get the specified layer.
*
* @param paraIndex
* The index of the layer.
***********************
*/
public CnnLayer getLayer(int paraIndex) throws RuntimeException{
if (paraIndex >= layers.size()) {
throw new RuntimeException("CnnLayer " + paraIndex + " is out of range: "
+ layers.size() + ".");
}//Of if
return layers.get(paraIndex);
}//Of getLayer
/**
***********************
* Get the output layer.
***********************
*/
public CnnLayer getOutputLayer() {
return layers.get(layers.size() - 1);
}//Of getOutputLayer
/**
***********************
* Get the number of layers.
***********************
*/
public int getNumLayers() {
return layers.size();
}//Of getNumLayers
}// Of class LayerBuilder 主要提供了一个List<>来装CnnLayer对象, 然后提供一些填装方法和获取方法, 一些越界的健壮性处理.
7. 核心代码: FullCnn类
在第3节我提到过, FullCnn类将完成四件大事:
- forward 预测
- backPropagation 设置惩罚信息
- 更新卷积核与偏差值
- 训练
在讲述这四件事情之前我们先要对于简单描述下本类需要的成员变量和一些初始化的过程.
7.1 成员变量与初始化
/**
* The value changes.
*/
private static double ALPHA = 0.85;
/**
* A constant.
*/
public static double LAMBDA = 0;
/**
* Manage layers.
*/
private static LayerBuilder layerBuilder;
/**
* Train using a number of instances simultaneously.
*/
private int batchSize;
/**
* Divide the batch size with the given value.
*/
private Operator divideBatchSize;
/**
* Multiply alpha with the given value.
*/
private Operator multiplyAlpha;
/**
* Multiply lambda and alpha with the given value.
*/
private Operator multiplyLambda;
成员变量都相对好理解, 一些本难以理解的部分在之前已经基本解释清楚了.
- ALPHA : 梯度下降方法中用于描述梯度下降幅度的梯度步长, 也可以理解为学习过程中的学习因子, 是个超参数, 可调.
- LAMBDA: 当卷积核矩阵进行更新时, 旧卷积核对于更新的影响程度, 可调.
- layerBuilder: CNN网络框架
- batchSize: batch训练中一个批次(batch)内的记录数
- divideBatchSize: 除batchSize值的单操作数数学运算的接口对象
- multiplyAlpha: 乘ALPHA值的单操作数数学运算的接口对象
- multiplyLambda: 乘LAMBDA值的单操作数数学运算的接口对象
这些单操作数数学运算接口的初始化如下:
/**
***********************
* Initialize operators using temporary classes.
***********************
*/
private void initOperators() {
divideBatchSize = new Operator() {
private static final long serialVersionUID = 7424011281732651055L;
@Override
public double process(double value) {
return value / batchSize;
}// Of process
};
multiplyAlpha = new Operator() {
private static final long serialVersionUID = 5761368499808006552L;
@Override
public double process(double value) {
return value * ALPHA;
}// Of process
};
multiplyLambda = new Operator() {
private static final long serialVersionUID = 4499087728362870577L;
@Override
public double process(double value) {
return value * (1 - LAMBDA * ALPHA);
}// Of process
};
}// Of initOperators本代码在主函数中创建CNN的结构, 按照CnnLayer与LayerBuilder的构造函数思想和布局以及2.1中我们确立的6层无全连接层的CNN参考模型可以建立下面的顺序代码:
LayerBuilder builder = new LayerBuilder();
builder.addLayer(new CnnLayer(LayerTypeEnum.INPUT, -1, new Size(28, 28)));
builder.addLayer(new CnnLayer(LayerTypeEnum.CONVOLUTION, 6, new Size(5, 5)));
builder.addLayer(new CnnLayer(LayerTypeEnum.SAMPLING, -1, new Size(2, 2)));
builder.addLayer(new CnnLayer(LayerTypeEnum.CONVOLUTION, 12, new Size(5, 5)));
builder.addLayer(new CnnLayer(LayerTypeEnum.SAMPLING, -1, new Size(2, 2)));
// output layer, digits 0 - 9.
builder.addLayer(new CnnLayer(LayerTypeEnum.OUTPUT, 10, null));
// Construct the full CNN.
FullCnn tempCnn = new FullCnn(builder, 10);这里提供的FullCnn本身的构造函数如下:
public FullCnn(LayerBuilder paraLayerBuilder, int paraBatchSize) {
layerBuilder = paraLayerBuilder;
batchSize = paraBatchSize;
setup();
initOperators();
}// Of the first constructor
简单来说就是给成员变量初始化, 这里的setup函数是给layerBuilder中的每一层按照给出的值参数以赋具体的空间和基本的矩阵初始化. 之前CnnLayer类中的构造函数提供的值更多是"定性"(指明空间大小与特性), 而到了FullCnn类的构造函数中, 才真正为CnnLayer类中定性的结构"定量"(开辟空间), 前者是后者的必要前导, 后者是前者的实现落实.
/**
***********************
* Setup according to the layer builder.
***********************
*/
public void setup() {
CnnLayer tempInputLayer = layerBuilder.getLayer(0);
tempInputLayer.initOutMaps(batchSize);
for (int i = 1; i < layerBuilder.getNumLayers(); i++) {
CnnLayer tempLayer = layerBuilder.getLayer(i);
CnnLayer tempFrontLayer = layerBuilder.getLayer(i - 1);
int tempFrontMapNum = tempFrontLayer.getOutMapNum();
switch (tempLayer.getType()) {
case INPUT:
// Should not be input. Maybe an error should be thrown out.
break;
case CONVOLUTION:
tempLayer.setMapSize(
tempFrontLayer.getMapSize().subtract(tempLayer.getKernelSize(), 1));
tempLayer.initKernel(tempFrontMapNum);
tempLayer.initBias();
tempLayer.initErrors(batchSize);
tempLayer.initOutMaps(batchSize);
break;
case SAMPLING:
tempLayer.setOutMapNum(tempFrontMapNum);
tempLayer.setMapSize(tempFrontLayer.getMapSize().divide(tempLayer.getScaleSize()));
tempLayer.initErrors(batchSize);
tempLayer.initOutMaps(batchSize);
break;
case OUTPUT:
tempLayer.initOutputKernel(tempFrontMapNum, tempFrontLayer.getMapSize());
tempLayer.initBias();
tempLayer.initErrors(batchSize);
tempLayer.initOutMaps(batchSize);
break;
}// Of switch
} // Of for i
}// Of setup看着长其实简单, 循环遍历每个层并且按照类别进行空间分配, 或者补充对于一些尚未定性的内容进行定性.
| Input Layer | Convolution Layer | Sampling Layer | Output Layer | |
| setMapSize | (Defined) | Subtract on the pre-layer mapSize | Divide on the pre-layer mapSize | (Defined) |
| setOutMapNum | (Defined) | (Defined) | Inherited from the pre-layer mapSize | (Defined) |
| initKernel | / | called | / | Done by the initOutputKernel |
| initBias | / | called | / | called |
| initErrors | / | called | called | called |
| initOutMaps | / | called | called | called |
7.2 训练
关于batch训练的内容我在6.1中已经说明, 下面就是代码的实现.
/**
***********************
* Train the cnn.
***********************
*/
public void train(Dataset paraDataset, int paraRounds) {
for (int t = 0; t < paraRounds; t++) {
System.out.println("Iteration: " + t);
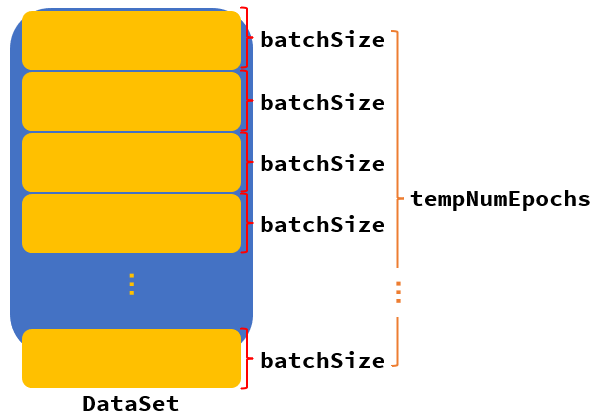
int tempNumEpochs = paraDataset.size() / batchSize;
if (paraDataset.size() % batchSize != 0)
tempNumEpochs++;
double tempNumCorrect = 0;
int tempCount = 0;
for (int i = 0; i < tempNumEpochs; i++) {
int[] tempRandomPerm = MathUtils.randomPerm(paraDataset.size(), batchSize);
CnnLayer.prepareForNewBatch();
for (int index : tempRandomPerm) {
boolean isRight = train(paraDataset.getInstance(index));
if (isRight)
tempNumCorrect++;
tempCount++;
CnnLayer.prepareForNewRecord();
} // Of for index
updateParameters();
if (i % 50 == 0) {
System.out.print("..");
if (i + 50 > tempNumEpochs)
System.out.println();
}
}
double p = 1.0 * tempNumCorrect / tempCount;
if (t % 10 == 1 && p > 0.96) {
ALPHA = 0.001 + ALPHA * 0.9;
} // Of iff
System.out.println("Training precision: " + p);
} // Of for i
}// Of train
- (Line 7) 外层大循环决定了单次训练由多少回合构成
- (Line 9-11) 确定了单个批次batch的大小, 通过数据集长度÷batchSize得到一共有多少batchSize, 确定为Epoch值. 有 Epoch * batchSize ≥ Dataset.size
- (Line 15) 按照Epoch值执行for循环, 保证所有批次batch都能被训练
- (Line 16) 获取tempRandomPerm数组, 表示一个批次内的记录号, 一个记录随机地与DataSet的某个数据下标对应, 批次内的记录号不重复.
- (Line 17-25) 依次获取一个批次内的所有记录号, 并且训练这个记录号对应的数据.
- (Line 27) 对于当前批次训练后的网络进行边权-卷积核 与 偏差的更新
- (Line 34-37) 梯度步长控制机制, 当循环到一定周期并且识别率高于某个阈值时降低梯度步长避免出现过拟合和梯度爆炸.
在具体训练某个批次内的记录是还调用了一个单参的重载train函数:
/**
***********************
* Train the cnn with only one record.
*
* @param paraRecord
* The given record.
***********************
*/
private boolean train(Instance paraRecord) {
forward(paraRecord);
boolean result = backPropagation(paraRecord);
return result;
}// Of train这里的result值是第一次训练后得到的预测值, 也就是forward的预测结果. CNN中的forward预测值集是一个张量, 若要返回一个确定的预测值必须要先将张量转换为向量. 本代码把这个操作放到backPropagation的第一步去执行了. 因此result是从backPropagation中传递出来的.
7.3 forward预测
/**
***********************
* Forward computing.
***********************
*/
private void forward(Instance instance) {
setInputLayerOutput(instance);
for (int l = 1; l < layerBuilder.getNumLayers(); l++) {
CnnLayer tempCurrentLayer = layerBuilder.getLayer(l);
CnnLayer tempLastLayer = layerBuilder.getLayer(l - 1);
switch (tempCurrentLayer.getType()) {
case CONVOLUTION:
setConvolutionOutput(tempCurrentLayer, tempLastLayer);
break;
case SAMPLING:
setSampOutput(tempCurrentLayer, tempLastLayer);
break;
case OUTPUT:
setConvolutionOutput(tempCurrentLayer, tempLastLayer);
break;
default:
break;
}// Of switch
} // Of for l
}// Of forward
输出层与卷积层的差异只是在设置卷积时的策略上, 而此后在forward过程中并没有特别大的差异,所以forward中卷积层与输出层都是调用setConvolutionOutput函数
要注意的就是forward的输入层的操作与其他都有一定不同(本文章CNN模型中输入层只有一张二值图, 而且这张二值图是以一个数组形式调入的), 因此专门使用setInputLayerOutput函数来实现.
/**
***********************
* Set the in layer output. Given a record, copy its values to the input
* map.
***********************
*/
private void setInputLayerOutput(Instance paraRecord) {
CnnLayer tempInputLayer = layerBuilder.getLayer(0);
Size tempMapSize = tempInputLayer.getMapSize();
double[] tempAttributes = paraRecord.getAttributes();
if (tempAttributes.length != tempMapSize.width * tempMapSize.height)
throw new RuntimeException("input record does not match the map size.");
for (int i = 0; i < tempMapSize.width; i++) {
for (int j = 0; j < tempMapSize.height; j++) {
tempInputLayer.setMapValue(0, i, j, tempAttributes[tempMapSize.height * i + j]);
} // Of for j
} // Of for i
}// Of setInputLayerOutputparaRecord是Instance类, 在提取了特征属性attributes[ ]后本质上是一个一维线性结构, 之后按照二维遍历的方式和一维转二维的公式\(h\times i+j\), 把attributes[ ] 转换到输入层唯一的切片上.
/**
***********************
* Compute the convolution output according to the output of the last layer.
*
* @param paraLastLayer
* the last layer.
* @param paraLayer
* the current layer.
***********************
*/
private void setConvolutionOutput(final CnnLayer paraLayer, final CnnLayer paraLastLayer) {
// int mapNum = paraLayer.getOutMapNum();
final int lastMapNum = paraLastLayer.getOutMapNum();
// Attention: paraLayer.getOutMapNum() may not be right.
for (int j = 0; j < paraLayer.getOutMapNum(); j++) {
double[][] tempSumMatrix = null;
for (int i = 0; i < lastMapNum; i++) {
double[][] lastMap = paraLastLayer.getMap(i);
double[][] kernel = paraLayer.getKernel(i, j);
if (tempSumMatrix == null) {
// On the first map.
tempSumMatrix = MathUtils.convnValid(lastMap, kernel);
} else {
// Sum up convolution maps
tempSumMatrix = MathUtils.matrixOp(MathUtils.convnValid(lastMap, kernel),
tempSumMatrix, null, null, MathUtils.plus);
} // Of if
} // Of for i
// Activation.
final double bias = paraLayer.getBias(j);
tempSumMatrix = MathUtils.matrixOp(tempSumMatrix, new Operator() {
private static final long serialVersionUID = 2469461972825890810L;
@Override
public double process(double value) {
return 1 / (1 + Math.pow(Math.E, -(value + bias)));
}
});
paraLayer.setMapValue(j, tempSumMatrix);
} // Of for j
}// Of setConvolutionOutput
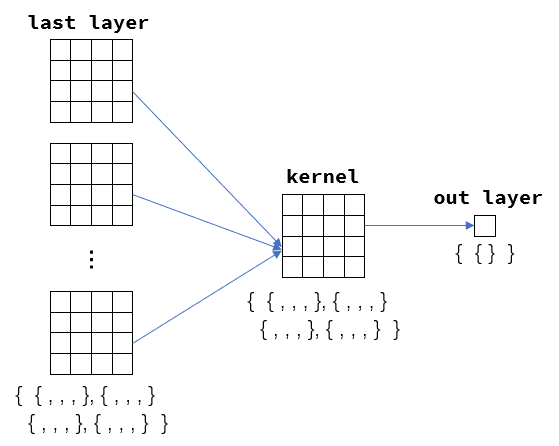
卷积层的forward操作. 还是代码长但是原理简单, 本质上确定一个本层映射\(j\), 然后遍历上一层全部切片并与之对应的卷积核(\(i\), \(j\))进行卷积操作, 然后把每次遍历得到的映射求和, 求和结果存于本层映射\(j\)之中.
需要留意, 在函数中额外声明了一个Operator接口对象用于实现单操作数的Sigmoid函数, 这也是接口本身的便捷之处, 能随时基于新的计算特点而创建临时的接口对象去实现特殊的操作. 常见的自定义Sort的cmp也是这个思路.
/**
***********************
* Compute the convolution output according to the output of the last layer.
*
* @param paraLastLayer
* the last layer.
* @param paraLayer
* the current layer.
***********************
*/
private void setSampOutput(final CnnLayer paraLayer, final CnnLayer paraLastLayer) {
// int tempLastMapNum = paraLastLayer.getOutMapNum();
// Attention: paraLayer.outMapNum may not be right.
for (int i = 0; i < paraLayer.outMapNum; i++) {
double[][] lastMap = paraLastLayer.getMap(i);
Size scaleSize = paraLayer.getScaleSize();
double[][] sampMatrix = MathUtils.scaleMatrix(lastMap, scaleSize);
paraLayer.setMapValue(i, sampMatrix);
} // Of for i
}// Of setSampOutput池化层的forward就更简单了, 只需要对单层的每个切片一对一映射就好了. getScaleSize获得本层的比例核, getMap(i) 获得上层第i个切片, 再通过MathUtils.scaleMatrix执行池化的得到池化后的矩阵sampMatrix, 最终通过setMapValue(i, sampMatrix)将这个池化后的矩阵设置到当前层的第i个映射位置.
7.3 backPropagation设置惩罚信息
/**
***********************
* Back-propagation.
*
* @param paraRecord
* The given record.
***********************
*/
private boolean backPropagation(Instance paraRecord) {
boolean result = setOutputLayerErrors(paraRecord);
setHiddenLayerErrors();
return result;
}// Of backPropagationbackPropagation与forward有个类似的一点, 就是他们的第一步操作总是要分离出来执行, 因为都具有一定的特殊性, backPropagation的第一步setOutputLayerErrors更是如此
/**
***********************
* Set errors of a sampling layer.
***********************
*/
private boolean setOutputLayerErrors(Instance paraRecord) {
CnnLayer tempOutputLayer = layerBuilder.getOutputLayer();
int tempMapNum = tempOutputLayer.getOutMapNum();
double[] tempTarget = new double[tempMapNum];
double[] tempOutMaps = new double[tempMapNum];
for (int m = 0; m < tempMapNum; m++) {
double[][] outmap = tempOutputLayer.getMap(m);
tempOutMaps[m] = outmap[0][0];
} // Of for m
int tempLabel = paraRecord.getLabel().intValue();
tempTarget[tempLabel] = 1;
for (int m = 0; m < tempMapNum; m++) {
tempOutputLayer.setError(m, 0, 0,
tempOutMaps[m] * (1 - tempOutMaps[m]) * (tempTarget[m] - tempOutMaps[m]));
} // Of for m
return tempLabel == MathUtils.getMaxIndex(tempOutMaps);
}// Of setOutputLayerErrorssetOutputLayerErrors首先要做的第一步就是完成forward没有完成的预测操作.
每层的切片我们都是以矩阵形式表示的, 那怕到了最后一层变为1*1的内容了, 这个矩阵结构还是一如既往. 因为我们所需要的预测值\(\hat{y}_i\)就存在于这个1*1矩阵的[0][0]位置. 因为之前在MathUtils类中编写的getMaxIndex是基于一维数组, 所以需要先把这个1*1矩阵中的[0][0]位置的元素提取到一维空间中, 这就是10~15行代码所做的事. 最终通过return返回了本次数据行训练的预测.
然后20~23行是对公式3的编写, 获得输出层的惩罚信息. 惩罚信息是1*1矩阵, 因此计算出来的值必须存放在[0][0]处.
/**
***********************
* Set errors of all hidden layers.
***********************
*/
private void setHiddenLayerErrors() {
// System.out.println("setHiddenLayerErrors");
for (int l = layerBuilder.getNumLayers() - 2; l > 0; l--) {
CnnLayer layer = layerBuilder.getLayer(l);
CnnLayer nextLayer = layerBuilder.getLayer(l + 1);
// System.out.println("layertype = " + layer.getType());
switch (layer.getType()) {
case SAMPLING:
setSamplingErrors(layer, nextLayer);
break;
case CONVOLUTION:
setConvolutionErrors(layer, nextLayer);
break;
default:
break;
}// Of switch
} // Of for l
}// Of setHiddenLayerErrorssetHiddenLayerErrors类似于forward函数, 遍历CNN网络并且按照type值调用不同的函数. 输出层已经执行过了, 输入层不需要backPropagation.
/**
***********************
* Set errors of a sampling layer.
***********************
*/
private void setConvolutionErrors(final CnnLayer paraLayer, final CnnLayer paraNextLayer) {
for (int m = 0; m < paraLayer.getOutMapNum(); m++) {
Size tempScale = paraNextLayer.getScaleSize();
double[][] tempNextLayerErrors = paraNextLayer.getError(m);
double[][] tempMap = paraLayer.getMap(m);
double[][] tempOutMatrix = MathUtils.matrixOp(tempMap, MathUtils.cloneMatrix(tempMap),
null, MathUtils.one_value, MathUtils.multiply);
tempOutMatrix = MathUtils.matrixOp(tempOutMatrix,
MathUtils.kronecker(tempNextLayerErrors, tempScale), null, null,
MathUtils.multiply);
paraLayer.setError(m, tempOutMatrix);
} // Of for m
}// Of setConvolutionErrors卷积层的惩罚信息需要利用卷积后一层的池化层的错误信息, 因此整个过程就是池化层向卷积层传递的过程. 卷积层流向池化层是池化(下采样), 那么这里自然就是反池化(上采样)代码.
循环遍历当前层得到任意切片\(j\), 同时也能对应地取得下一层的切片\(j\), 这是池化的特征决定的. 然后你会发现2.3.4中的公式7中的全部参数你都知道了, 于是直接运算就好了.
12行的函数是对于公式7的激活函数的求导部分的编写, 这里就用到了我们提到过的(1 - A)算子, 14行的函数中调用了反池化函数kronecker, 是公式7的upsample部分.
/**
***********************
* Set errors of a sampling layer.
***********************
*/
private void setSamplingErrors(final CnnLayer paraLayer, final CnnLayer paraNextLayer) {
// int mapNum = layer.getOutMapNum();
int tempNextMapNum = paraNextLayer.getOutMapNum();
// Attention: getOutMapNum() may not be correct
for (int i = 0; i < paraLayer.getOutMapNum(); i++) {
double[][] sum = null;
for (int j = 0; j < tempNextMapNum; j++) {
double[][] nextError = paraNextLayer.getError(j);
double[][] kernel = paraNextLayer.getKernel(i, j);
if (sum == null) {
sum = MathUtils.convnFull(nextError, MathUtils.rot180(kernel));
} else {
sum = MathUtils.matrixOp(
MathUtils.convnFull(nextError, MathUtils.rot180(kernel)), sum, null,
null, MathUtils.plus);
} // Of if
} // Of for j
paraLayer.setError(i, sum);
} // Of if
} // Of for i
}// Of setSamplingErrors池化层的惩罚信息需要利用池化后一层的卷积层的错误信息, 因此整个过程就是卷积层向池化层传递的过程. 池化层流向卷积层是卷积操作(Valid模式卷积), 那么这里自然就是反卷积(Full模式卷积)代码.
外层关于i的遍历优先固定paraLayer中一个切片位置\(i\), 然后内部关于j的遍历可以后续确定某个paraNextLayer的切片位置与某个惩罚信息\(e^{l+1}_{i}\), 以及一个卷积核\(K_{ij}\), 由此2.3.3中的公式4就可以编写了. 最终对j的遍历实现求和的全覆盖, 求和结果矩阵作为切片\(i\)的惩罚信息.
注意调用公式4时内部使用的是Full模式卷积.
7.4 更新边权与偏差
/**
***********************
* Update parameters.
***********************
*/
private void updateParameters() {
for (int l = 1; l < layerBuilder.getNumLayers(); l++) {
CnnLayer layer = layerBuilder.getLayer(l);
CnnLayer lastLayer = layerBuilder.getLayer(l - 1);
switch (layer.getType()) {
case CONVOLUTION:
case OUTPUT:
updateKernels(layer, lastLayer);
updateBias(layer, lastLayer);
break;
default:
break;
}// Of switch
} // Of for l
}// Of updateParameters更新边权的操作只隶属于卷积层与池化层或者池化层与输出层之间, 因为只有这两层之间存在可设置的卷积核与激活函数.
/**
***********************
* Update kernels.
***********************
*/
private void updateKernels(final CnnLayer paraLayer, final CnnLayer paraLastLayer) {
int tempLastMapNum = paraLastLayer.getOutMapNum();
for (int j = 0; j < paraLayer.getOutMapNum(); j++) {
for (int i = 0; i < tempLastMapNum; i++) {
double[][] tempDeltaKernel = null;
for (int r = 0; r < batchSize; r++) {
double[][] error = paraLayer.getError(r, j);
if (tempDeltaKernel == null)
tempDeltaKernel = MathUtils.convnValid(paraLastLayer.getMap(r, i), error);
else {
tempDeltaKernel = MathUtils.matrixOp(
MathUtils.convnValid(paraLastLayer.getMap(r, i), error),
tempDeltaKernel, null, null, MathUtils.plus);
} // Of if
} // Of for r
tempDeltaKernel = MathUtils.matrixOp(tempDeltaKernel, divideBatchSize);
double[][] kernel = paraLayer.getKernel(i, j);
tempDeltaKernel = MathUtils.matrixOp(kernel, tempDeltaKernel, multiplyLambda,
multiplyAlpha, MathUtils.plus);
paraLayer.setKernel(i, j, tempDeltaKernel);
} // Of for i
} // Of for j
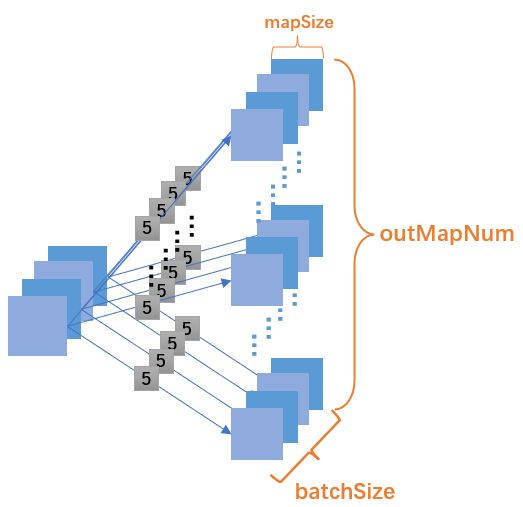
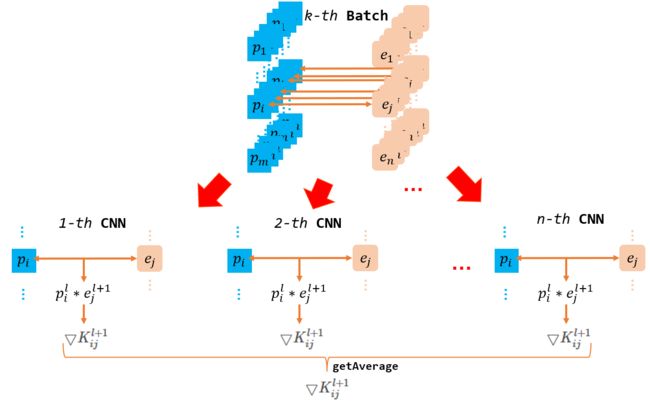
}// Of updateKernels2.4节中的公式8只给出了一套神经网络中的卷积核改变量, 在batch训练中同个批次内有多个记录数, 每个记录都代表一套CNN神经网络, 都有自己的惩罚信息. 因此我们在计算\(l\)层到\(l+1\)层的惩罚信息时可以将同批次内每套CNN神经网络在这两层之间计算得到的更新卷积核加起来求平均.
第二张图最终得到的\(\bigtriangledown K^{l+1}_{ij} \)就是我们希望的边权. 这就是为什么代码中会额外套一层batchSize的循环以及25行的中的divideBatchSize运算.
最终使用公式9, 通过setKernel( ) 方法完成卷积核重设.
/**
***********************
* Update bias.
***********************
*/
private void updateBias(final CnnLayer paraLayer, CnnLayer paraLastLayer) {
final double[][][][] errors = paraLayer.getErrors();
for (int j = 0; j < paraLayer.getOutMapNum(); j++) {
double[][] error = MathUtils.sum(errors, j);
double deltaBias = MathUtils.sum(error) / batchSize;
double bias = paraLayer.getBias(j) + ALPHA * deltaBias;
paraLayer.setBias(j, bias);
} // Of for j
}// Of updateBias明白卷积核的设置后, 偏差值设置的第11行突然÷batchSize也变得可以理解了.
按照2.4节的公式10可知, 理论上, 我们只需要把当前层的第j个惩罚信息矩阵内的全部元素加起来就可以得到当前层的第j个偏差值梯度\(\bigtriangledown b^{l}_{j}\). 而最终确定的偏差值梯度就是与batch内每个CNN网络中此位置求得的偏差变化量的求和再平均.
代码中, 第10行的sum是对于同batch批次所有神经网络的paraLayer层中的第j个惩罚信息求和, 而第11行的sum是单纯的矩阵内元素求和, 返回一个数组, 最终除以batchSize求平均. 这个操作与我们的描述是等价的.
最终使用公式10, 通过setBias( ) 方法完成卷积核重设.
8. 运行效果测试
/**
***********************
* The main entrance.
***********************
*/
public static void main(String[] args) {
LayerBuilder builder = new LayerBuilder();
builder.addLayer(new CnnLayer(LayerTypeEnum.INPUT, -1, new Size(28, 28)));
builder.addLayer(new CnnLayer(LayerTypeEnum.CONVOLUTION, 6, new Size(5, 5)));
builder.addLayer(new CnnLayer(LayerTypeEnum.SAMPLING, -1, new Size(2, 2)));
builder.addLayer(new CnnLayer(LayerTypeEnum.CONVOLUTION, 12, new Size(5, 5)));
builder.addLayer(new CnnLayer(LayerTypeEnum.SAMPLING, -1, new Size(2, 2)));
// output layer, digits 0 - 9.
builder.addLayer(new CnnLayer(LayerTypeEnum.OUTPUT, 10, null));
// Construct the full CNN.
FullCnn tempCnn = new FullCnn(builder, 10);
Dataset tempTrainingSet = new Dataset("d:/Java DataSet/train.format", ",", 784);
// Train the model.
tempCnn.train(tempTrainingSet, 10);
}// Of main图中的每个区域都是一次完整训练得到的训练结果, 可以明显发现, 最终识别的效率还是比较可观的, 在第二次训练时就能达到0.9以上.
为了进一步验证代码的正确性, 我使用了做CNN的大家都喜闻乐见的mnist数据集来辅助测试.
MNIST 数据集是美国国家标准与技术研究所(National Institute of Standards and Technology,简称NIST)制作的一个非常简单的数据集。其内容是一些手写的阿拉伯数字(0到9十个数字)。
mnist测试集有60,000个训练样本和10,000个测试样本, 我首先将我训练的CNN网络跑了一遍mnist的测试集, 效果还不错:
然后再次训练, 并且每轮训练后同时随机2000个mnist测试样本再进行测试有如下情况:
可以发现过拟合线性并不是特别严重, 可能是训练集量不大的缘故? 毕竟train.format 只有12001个数据. 但是, 实际上扩大了数据集数量还是没有很明显的过拟合:
原因我猜测估计还是和网络的设置有关的吧, 毕竟本文的网络只有6层, 而且并没有全连接部分, 于是整体还算简单, 拟合并不是非常严格(手写体数字现在很多高的拟合网络在训练集中完全可以做到1.0)
以上就是本文想表达的CNN的全部内容了! 本人也是初学CNN, 略有不足欢迎大家指正.