算法笔记(六):差分法
(6)差分法
目录
一、差分
1、介绍
2、定义
3、差分与前缀和
二、一维差分
1、定义
2、作用
3、方法
接下来是实战演练!!!
三、二维差分
1、定义
2、作用
3、方法
接下来是实战演练!!!
结论
写在最后!!!
一、差分
1、介绍
一般地,差分主要用于让一个序列某一特定范围内的所有值都加上或减去一个常数。
所以差分往往应用于线性的场合,即一维数组的环境,但是除此之外,差分还可以应用于二维数组,但是相比较一维数组,应用的较少。
2、定义
差分可以简单的看成序列中每个元素与其前一个元素的差。
3、差分与前缀和
const int N = 100010;
int n; //n数组长度
//定义两个一维整形数组 a为原数组,b为差分数组
int a[N],b[N];
//根据定义可知
b[i] = a[i] - a[i-1];
//稍微具体
b[1] = a[1];
b[2] = a[2] - a[1];
b[3] = a[3] - a[2];
...
b[i] = a[i] - a[i-1];
//转化一下,求数组b的前缀和,根据上面公式可得
b[1]+b[2]+b[3]+...+b[i]
= a[1]+(a[2]-a[1])+(a[3]-a[2])+...+(a[i]-a[i-1])
= a[i]
//由此可知,原序列为差分序列的前缀和序列
a[i] = b[1]+b[2]+b[3]+...+b[i];
一般地,我们认为原序列就是差分序列的前缀和,所以把差分看做前缀和的逆运算
二、一维差分
1、定义
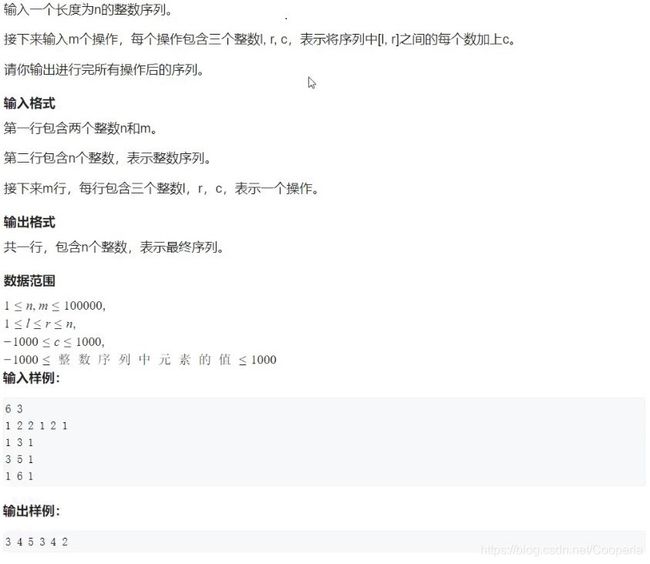
一维差分是指给定一个长度为n的序列a,要求支持操作pro(l,r,c)表示对a[l]~a[r]区间上的每一个值都加上或减去常数c,并求修改后的序列a。
2、作用
让一个序列中某个区间内的所有值均加上或减去一个常数。
可以将对a数组任意区间的同一操作优化到O(1)。
//区间[l,r]中的所有值都加上常数c
b[l] += c;
b[r+1] -= c;
//上边语句实现原理 b相当于a的辅助数组
//把a序列分为[1,l-1],[l,r],[r+1,n]三部分,由差分定义和与前缀和关系可得
a[l-1] = b[1]+b[2]+...+b[l-1]; //b[1]~b[l-1]中所有值都未改变,a[l-1]也不变
a[l] = b[1]+b[2]+...+b[l-1]+b[l]; //b[1] += c,所以a[l] += c
a[l+1] = b[1]+b[2]+...+b[l-1]+b[l]+b[l+1]; //b[1] += c,所以a[l+1] += c
... //一直到
a[r] = b[1]+b[2]+...b[l]+...+b[r]; //b[1] += c,所以a[l+1] += c
a[r+1] = b[1]+b[2]+...b[l]+...+b[r]+b[r+1]; //b[l] += c,b[r+1] -= c;所以a[r+1]不变
//所以由此可知上面的两个语句(b[l] += c;b[r+1] -= c)可以实现a数组在区间[l,r]内的所有值都加上了常数c
3、方法
对a数组区间[l,r]同时加上c的操作可转化为:
void insert(int l, int r, int c)
{
b[l] += c;
b[r+1] -= c;
}
while(m--)
{
int l,r,c;
scanf("%d%d%d",&l,&r,&c);
insert(l,r,c);
}对b数组求前缀和即可得到原数组a:
for(int i = 1; i <= n; i++)
{
b[i] += b[i-1];
printf("%d ",b[i]);
}接下来是实战演练!!!
题目:
代码:
#include
using namespace std;
const int N = 100010;
int n,m;
int a[N],b[N];
void insert(int l, int r, int c)
{
b[l] += c;
b[r+1] -= c;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i = 1; i <= n; i++)
{
scanf("%d",&a[i]);
}
//插入
for(int i = 1; i <= n; i ++)
{
insert(i,i,a[i]);
}
while(m--)
{
int l,r,c;
scanf("%d%d%d",&l,&r,&c);
insert(l,r,c);
}
for(int i = 1; i <= n; i++)
{
b[i] += b[i-1];
printf("%d ",b[i]);
}
return 0;
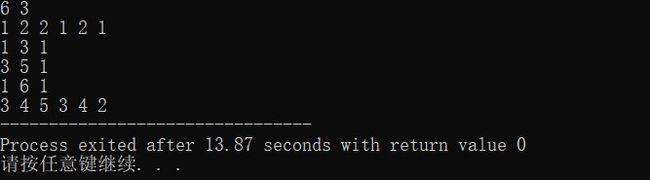
} 结果:
三、二维差分
1、定义
二维差分是指对于一个n*m的矩阵a,要求支持操作pro(x1,y1,x2,y2,a),表示对于以(x1,y1)为左上角,(x2,y2)为右下角的矩形区域,每个元素都加上常数a。求修改后的矩阵a。
2、作用
与一维差分一样二维差分可以把对矩阵的同一操作优化到O(1)。
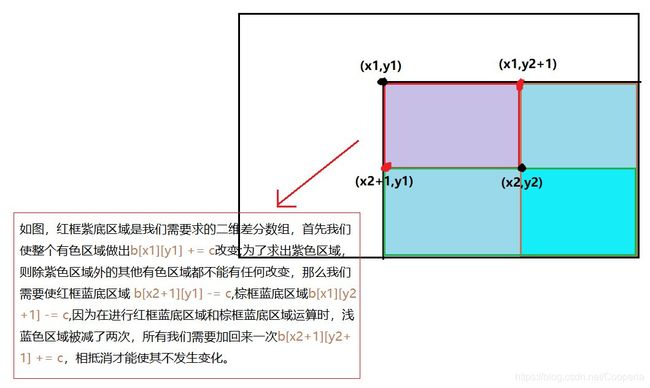
图解:
3、方法
紫色矩形区域同时加上一个常数,由图可以得到插入函数:
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1] += c;
b[x2+1][y1] -= c;
b[x1][y2+1] -= c;
b[x2+1][y2+1] += c;
}初始化可以视为在(i,j)和(i,j)的小矩形内插入a[i][j];
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
insert(i,j,i,j,a[i][j]);
}
}对二维差分数组求二维前缀和可以得到原数组:
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];
printf("%d ",b[i][j]);
}
puts("");
}接下来是实战演练!!!
题目:
代码:
#include
using namespace std;
const int N = 1010;
int n,m,q;
int a[N][N],b[N][N];
void insert(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1] += c;
b[x2+1][y1] -= c;
b[x1][y2+1] -= c;
b[x2+1][y2+1] += c;
}
int main()
{
scanf("%d%d%d",&n,&m,&q);
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
scanf("%d",&a[i][j]);
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
insert(i,j,i,j,a[i][j]);
}
}
while(q--)
{
int x1,y1,x2,y2,c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1,y1,x2,y2,c);
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1];
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
printf("%d ",b[i][j]);
}
puts("");
}
return 0;
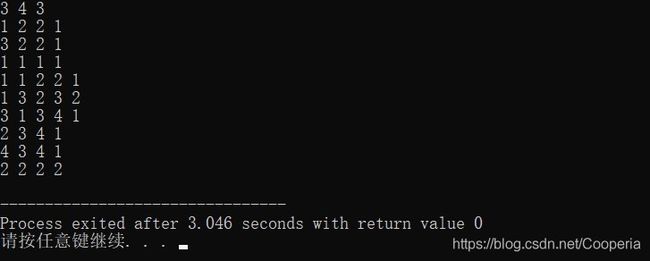
} 结果:
结论
树状数组插入和查询都可以优化到O(logn)。差分和前缀和适合用在查询或修改次数十分巨大的时候,当修改和查询在同一复杂度时适合用树状数组。
写在最后!!!
这是做的acwing创始人闫神讲的学习视频笔记,但是作为算法小白,知识还很不牢固。如果有错误请欢迎指正~~,感谢!!!