对数图像、极坐标图像、柱状图、散点图、3D图像简单绘制

对数图像函数

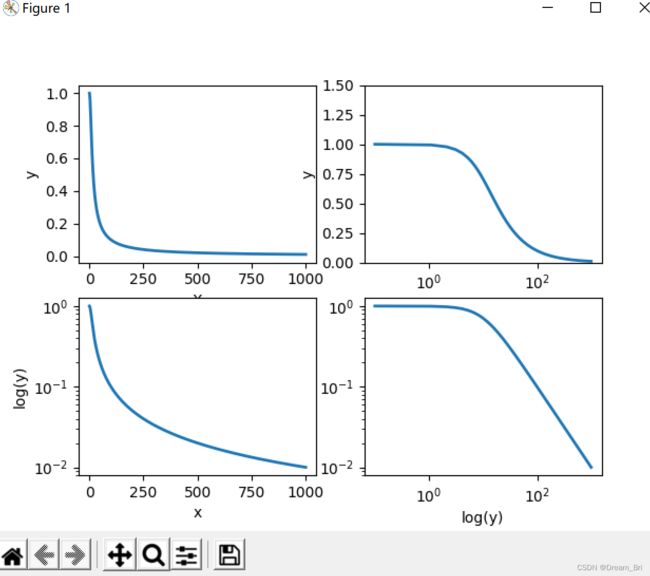
对数函数绘制设计三个函数，解析如下：

semilogx(x1, y1)：半对数函数，x变为常用对数刻度，y轴仍是线性刻度。

semilogy(x1, y1)：半对数函数，x仍是线性刻度，y轴变为常用对数刻度。

loglog(x1, y1)：全对数函数，x，y都变为常用对数刻度。

代码显示如下：

import numpy as np
import matplotlib.pyplot as plt

w = np.linspace(0.1, 1000, 1000)
p = np.abs(1 / (1 + 0.1j * w))

plt.subplot(221)
plt.plot(w, p, lw=2)
plt.xlabel('X')
plt.ylabel('y')

plt.subplot(222)
plt.semilogx(w, p, lw=2)
# ylim具有设置y坐标轴范围的作用
plt.ylim(0, 1.5)
plt.xlabel('log(X)')
plt.ylabel('y')

plt.subplot(223)
plt.semilogy(w, p, lw=2)
# plt.ylim(0, 1.5)
plt.xlabel('x')
plt.ylabel('log(y)')

plt.subplot(224)
plt.loglog(w, p, lw=2)
plt.xlabel('log(x)')
plt.xlabel('log(y)')
plt.show()

显示结果如下：

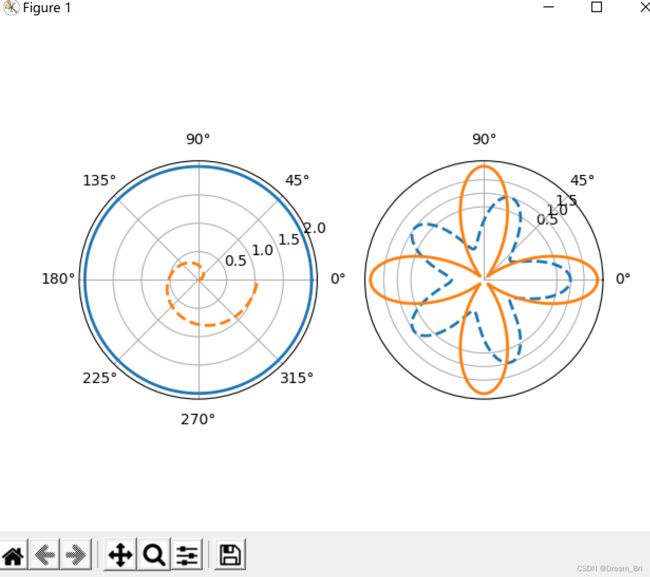
极坐标图像显示

代码显示：

import numpy as np
import matplotlib.pyplot as plt

theta = np.arange(0, 2 * np.pi, 0.02)
plt.subplot(121, polar=True)
plt.plot(theta, 2 * np.ones_like(theta), lw=2)
plt.plot(theta, theta / 6, '--', lw=2)
plt.subplot(122, polar=True)
plt.plot(theta, np.cos(5 * theta), '--', lw=2)
plt.plot(theta, 2 * np.cos(4 * theta), lw=2)
plt.rgrids(np.arange(0.5, 2, 0.5), angle=45)
plt.thetagrids([0, 45, 90])
plt.show()

图像显示如下：

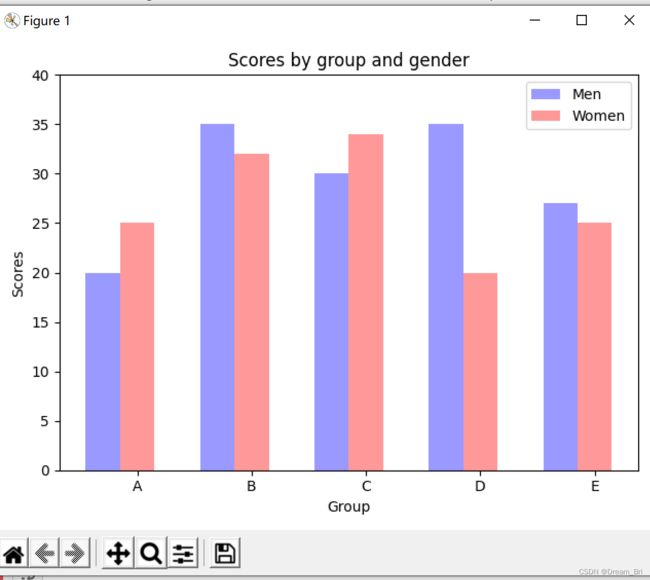
柱状图图像显示

代码显示为：

import numpy as np
import matplotlib.pyplot as plt


n_groups = 5
means_men = (20, 35, 30, 35, 27)
means_women = (25, 32, 34, 20, 25)
fig, ax = plt.subplots()
index = np.arange(n_groups)
bar_width = 0.3
opacity = 0.4
rects1 = plt.bar(index, means_men, bar_width, alpha=opacity, color='b', label='Men')
rects2 = plt.bar(index + bar_width, means_women, bar_width, alpha=opacity, color = 'r', label = 'Women')
plt.xlabel('Group')
plt.ylabel('Scores')
plt.title('Scores by group and gender')
plt.xticks(index + bar_width, ('A', 'B', 'C', 'D', 'E'))
plt.ylim(0, 40)
plt.legend()
plt.tight_layout()
plt.show()

图像显示为：

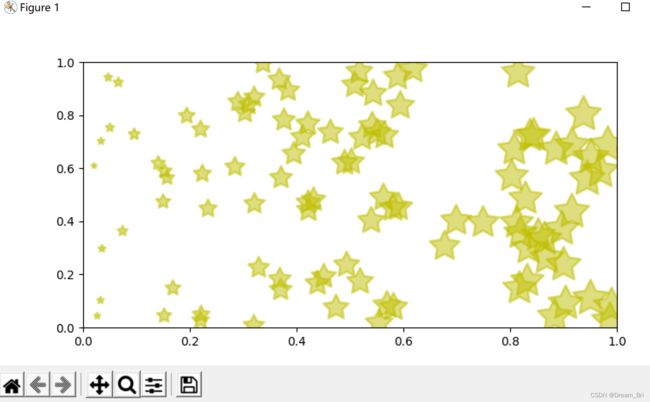
散点图图像显示

import numpy as np
import matplotlib.pyplot as plt


plt.figure(figsize=(8, 4))
x = np.random.random(100)
y = np.random.random(100)
plt.scatter(x, y, s=x * 1000, c='y', marker=(5, 1), alpha=0.5, lw=2, facecolors='none')
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.show()

图像显示

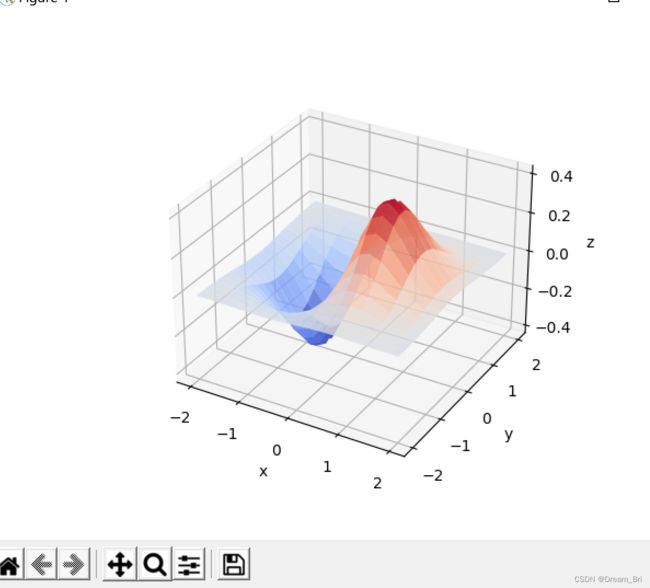
3D图像显示

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d

x, y = np.mgrid[-2:2:20j, -2:2:20j]
z = x * np.exp(-x ** 2 - y ** 2)
ax = plt.subplot(111, projection='3d')
ax.plot_surface(x, y, z, rstride=2, cstride=1, cmap=plt.cm.coolwarm, alpha=0.8)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

图像显示如下：

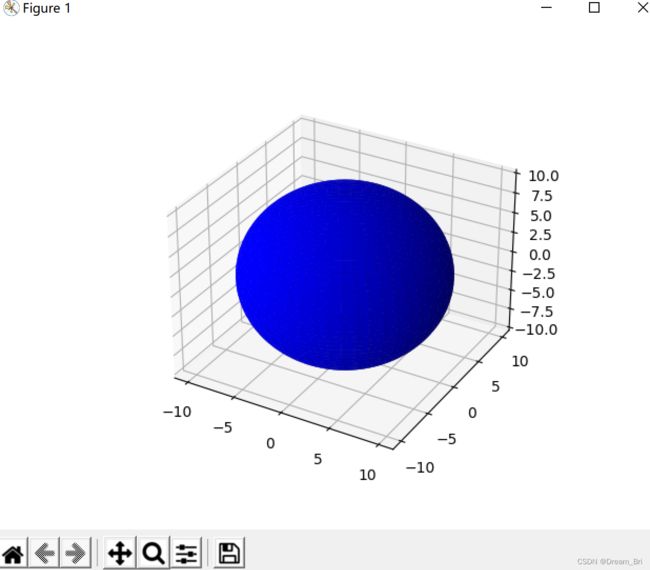
3D椭球绘制

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Make data
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
x = 10 * np.outer(np.cos(u), np.sin(v))
y = 10 * np.outer(np.sin(u), np.sin(v))
z = 10 * np.outer(np.ones(np.size(u)), np.cos(v))

# Plot the surface
ax.plot_surface(x, y, z, color='b')

plt.show()

图像显示：

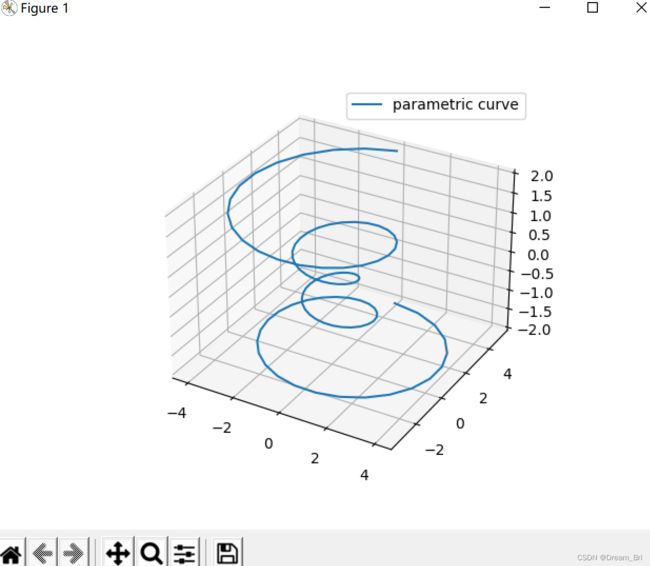
3D螺旋线绘制

import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt

mpl.rcParams['legend.fontsize'] = 10

fig = plt.figure()
ax = fig.gca(projection='3d')
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z ** 2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)
ax.plot(x, y, z, label='parametric curve')
ax.legend()

plt.show()

图像显示：

原文链接：
https://blog.csdn.net/Mrweng1996/article/details/104352645
https://blog.csdn.net/guduruyu/article/details/78050268
https://blog.csdn.net/ikerpeng/article/details/20523679
《matplotlib手册》