数据结构—堆(完全解析)
数据结构—堆(完全解析)
数据结构——堆(Heap)大根堆、小根堆
详解数据结构——堆
堆的基本存储
【从堆的定义到优先队列、堆排序】 10分钟看懂必考的数据结构——堆
【堆/排序】堆排序的两种建堆方法
【算法】排序算法之堆排序
C++:浅析STL之priority_queue构建大根堆与小根堆
基本概念
堆通常是一个可以被看做一棵完全二叉树的数组对象
堆满足下列性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树
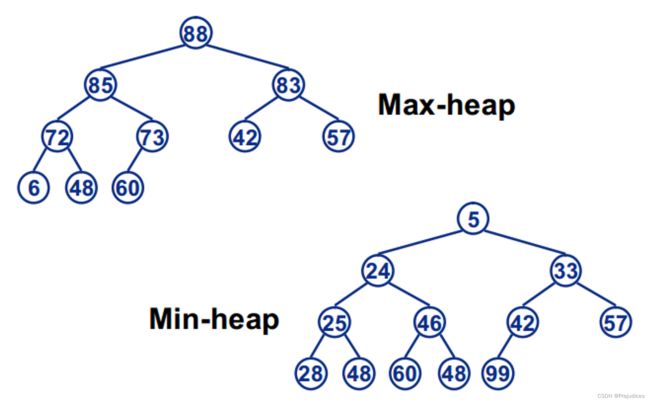
Min-heap(大根堆): 父节点的值小于或等于子节点的值
Max-heap(小根堆): 父节点的值大于或等于子节点的值
堆的存储
一般都用数组来表示堆,i结点的父结点下标就为(i–1)/2
它的左右子结点下标分别为2 * i + 1和2 * i + 2
如第0个结点左右子结点下标分别为1和2
堆的插入和上浮
- 当一个新元素想要插入这个堆的时候,我们首先把他放到这个堆的末尾
- 然后依据堆的特性,对它的位置进行调整,由于要保持父结点的值要永远少于其子节点的值,而
2的直接父节点6大于了它,所以要把他们两的位置对换 - 对换完毕后,再检查这个堆的状态,发现其父节点
3仍然大于自己,所以继续往上和3对换 - 结束后和
0比较,0不大于自己,所以停留在原地不动,插入结束 - 简单来说,插入一个结点就是将该元素插入到堆的尾部,然后不断上浮调整位置,直至满足堆的条件
堆的删除和下沉
- 删除一般指的都是删除堆顶元素,在堆顶元素被拿掉后,将末尾元素置换上来,进行下沉操作
- 由于这是最小堆,堆顶一定是最小元素,首先
6大于左结点1,需要下沉, - 下沉完以后继续和它子节点比较,发现左结点
2小于自身,继续下沉 - 最后
8和9都比6大,停止下沉。 - 总结来说,意思就是删除堆顶元素后,用末尾元素补上,然后不断下沉,直至满足堆的条件
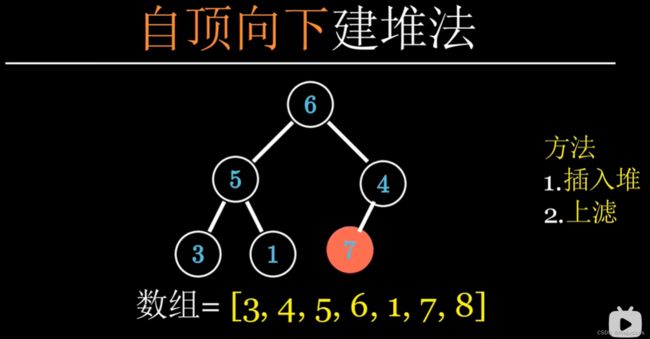
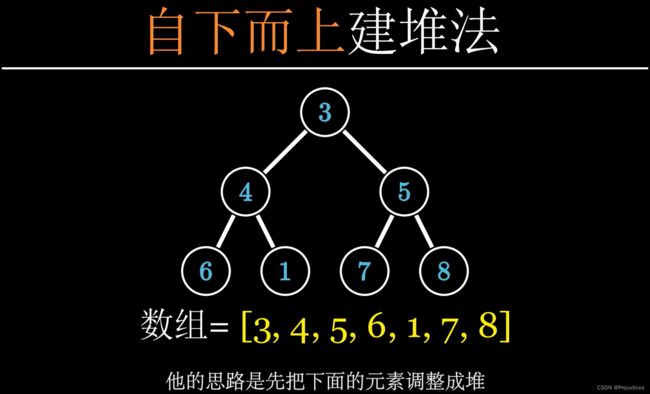
堆的建立
自顶向下,时间复杂度为O(nlogn)
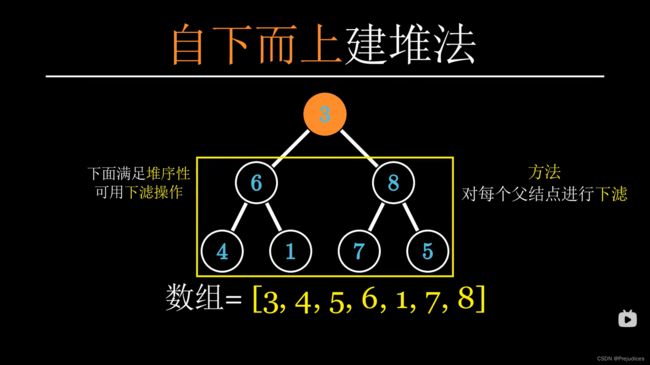
从倒数第二排开始,对每一个父节点进行下滤操作,直到根节点操作完毕
堆的应用
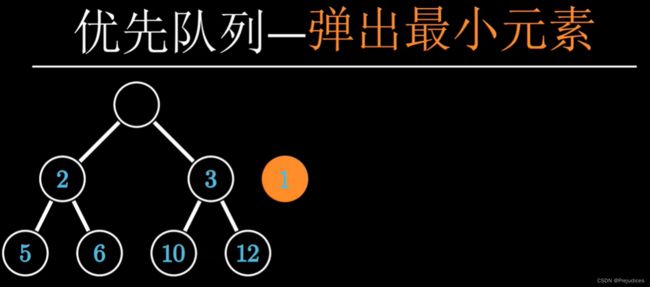
优先队列
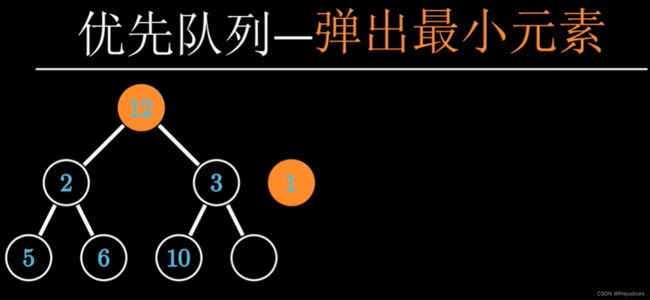
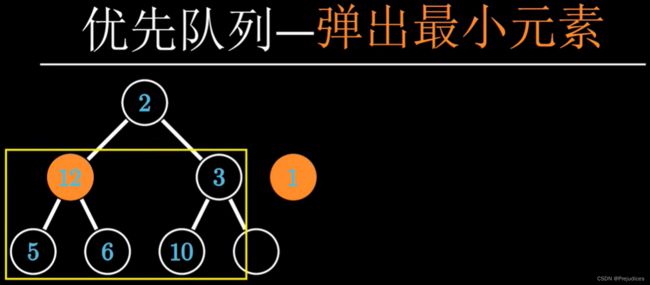
优先队列有两个操作,插入队列和弹出最小元素
优先队列利用小根堆实现,弹出根节点即可实现弹出最小元素的操作
弹出后要将剩余的元素调整为堆,将最后一个元素放到根节点,进行下沉操作即可
堆排序
- 先把数组构造成一个大顶堆(父亲节点大于其子节点),然后把堆顶(数组最大值,数组第一个元素)和数组最后一个元素交换,这样就把最大值放到了数组最后边
- 把数组度-1,再进行构造堆把剩余的第二大值放到堆顶,输出堆顶(放到剩余未排序数组最后面),依次类推,直至数组排序完成
#include C++ STL大根堆小根堆
在C++中优先队列默认的是大根堆,如果用小根堆则加入greater
#include 支持的顺序容器:vector,queue,默认是vector
priority_queue类能按照有序的方式在底层数据结构中执行插入、删除操作
q.pop();//删除优先队列priority_queuel的最高优先级元素(通过调用底层容器的pop_back()实现)
q.push(item);//在priority._queue优先级顺序合适的位置添加创建一个值为item的元素(通过调用底层容器的push_back()操作实现)
q.emplace(args);//在priority_queue优先级顺序合适的位置添加个由args构造的元素(通过调用底层容器的emplace_back()操作实现)
q.top();//返回priority_queue的首元素的引用(通过调用底层容器的front()操作实现)
q.empty();//判断q是否为空,空返回true,否则返回false(通过调用底层容器的empty()操作实现)
q.size();//返回q中的元素个数(通过调用底层容器的size()操作实现)
swap(q,p);//交换两个优先队列priority_queue p,q的内容,p和q的底层容器类型也必须相同(通过调用底层容器的swap0操纵实现)