移动通信客户价值数据挖掘分析实战

本实战案共分为五个部分：商业背景、指标设计、部署环境、数据准备、回归分析，其中回归分析包括：模型构建、模型诊断、模型结果、模型应用。

©️数据STUDIO投稿 · 作者｜玄武

1.商业背景

众所周知，移动通信市场已经日趋饱和，增加规模已经变得异常艰难，通信运营商互挖墙角已经成为家常便事。很多消费者，今天还是中国移动的客户，明天只要中国电信给点好处，就变成中国电信的客户，后天一看中国联通推出打折促销活动，又变成中国联通的客户，再过几天，中国移动稍微关怀一下，又重新回到中国移动的怀抱。在这样一个周而复始的拉锯战中，通信运营商耗尽了有限的营销资源，客户也没有得到实质性的好处，因为更换运营商其实也是一种消耗。此时，增强客户的忠诚度，提升公司的盈利能力，对通信运营商来说，就变得非常重要。

对于兵家必争的高校大学生市场，某通信运营商针对大学生群体，推出了校园网计划来提升客户忠诚度。按照校园网运营规则，如果一名大学生希望加入校园网，他首先必须是该运营商的用户，否则无法参加该计划，此外，还得由现有校园网用户进行邀请。作为回报，校园网内所有通话资费非常便宜，而且数据流量优惠也非常巨大，但与网外朋友通信资费照旧。所以，为了降低自身资费，现有校园网成员都有很大动力邀请朋友加入校园网。这样的话，大量的日常沟通将发生在校园网内，这不仅降低了通信资费，还享受了更好的沟通服务，同时，已经加入校园网的成员则发现很难离开，因为大部分朋友以及主要通信社交网络都在校园网中，个人一旦离开，如果还想保持跟过去一样的沟通强度，成本将非常昂贵。

那么，通信运营商的付出与回报又如何呢？为了深度“套牢”在校大学生客户，运营商有着重要的付出，也就是降低资费。此外，为了迅速扩张校园网，鼓励大家推荐新客户，运营商对推荐者有一定的奖励，比如奖励话费或者流量甚至现金。

那么，通信运营商付出这么多，希望得到的回报是什么呢？

第一个回报，高忠诚度、低离网率。既然用户把好友都拉进了校园网，那么用户的主要通信社交网络都被校园网覆盖，这能否增加忠诚度，降低离网率，进而间接降低客户的获取和维护成本？

第二个回报，总利润不降反升。虽然下调了资费，但是，资费的下调很可能会刺激消费量的上升，从而使得最终总利润不降反升。

但是，运营一段时间后发现，好消息是离网率确实下降不少、总利润也有所上升，坏消息是总利润上升低于预期。因为有些校园网用户邀请了很多低端客户进来，这些低端客户的总消费量并没有因为入网而有任何上升，相反，由于资费的下降，他们给公司贡献的收入却大幅下降。但是，也有些校园网用户邀请了很多优质客户进来，相比入网前，这些优质客户的沟通更加密切，因此，尽管单位时长的资费水平下降很多，但是他们对企业的总利润贡献却上升不少。

这说明，不同的客户作为推荐者，能带来的被推荐者的价值是不一样的，也就是说，并非每个人都能推荐有价值的客户，甚至有些推荐者带来的客户的贡献是负的。因为，一名被推荐进来的客户，他对校园网贡献的大小，除依赖自身特征外，还极大地依赖于推荐者，如果推荐者是话痨，被推荐者很可能就是那个被话痨的对象，如果推荐者是个游戏高手，被推荐者很可能就是他游戏中的猪队友。因此，有必要研究，带来低价值客户的推荐者与带来高价值客户的推荐者之间有没有系统性差异？如果能够掌握此规律，就可把有限的奖励资源，有针对性地投放到那些能为企业带来高价值客户的推荐者身上。

因此，需要详细研究：什么样的推荐者能够带来高价值客户，什么样的推荐者带来的客户是低价值客户？

2.指标设计

这个时候，我们就需要设计一个指标来衡量推荐者的价值，并且这个指标必须对业务有好的指导意义。那么，推荐者的价值应当通过什么指标来评估呢？这个指标就是我们研究的因变量。我相信，大家可以找出不少指标来评估推荐者的价值，比如，推荐者所推荐的所有客户，在加入校园网后，其绝对和相对收入的增长或者绝对和相对利润的增长，在这里，我们使用“某推荐者当月推荐的所有客户加入校园网后次月的利润环比增长率”为评估指标，也就是为我们研究的因变量。

在确定因变量之后，我们则需要考虑有哪些因素会影响着推荐者的价值，也就是需要寻找自变量。在实际工作中，我们有大量的有用指标，能够详细地刻画推荐者的方方面面。比如，可以考虑消费者的消费行为，主要包括该用户在各项通信及增值业务上的花费。再比如，还可以考虑消费者的通话特征，包括该用户的通话时长、频率、时间等，甚至还可以将通话时长拆分成主叫、被叫、本地、长途、漫游等。总而言之，实际工作中可考虑的指标很多，它们都有助于更好地描述推荐者，它们都可以成为自变量。在这里，纯粹为了简单起见，只考虑这么三个自变量。

第一个自变量，月通话总量

月通话总量，指该推荐者进行推荐的当月的通话总时长，以百分钟计。很显然，这是个重要的自变量，它直接刻画了用户的活跃程度。由于校园网提供非常优惠的通话资费，因此对那些通话总量高的用户很有吸引力，假设高通话量用户的好友也可能是高通话量用户，那么，具有高通话量特征的推荐者就更有可能带来优质客户。

第二个自变量，大网占比

大网指的是该运营商的通信网络，大网占比，就是在该推荐者推荐当月的通话总时长中，发生在该运营商网内的通话总时长占比。这个占比越高，说明该推荐者的通话，越多地发生在该运营商生态体系之内，因此，他具有更好的基础为校园网计划拉新客户。

第三个自变量，小网占比

小网指的是校园网，小网占比，就是在该推荐者推荐当月发生在该运营商网内的通话总时长中，发生在校园网内的通话总时长占比。

大网占比，衡量了推荐者全部通话中有多少发生在该运营商网内，小网占比衡量的则是发生在该运营商网内的通话时长中，又有多少发生在校园网。由于加入校园网的前提条件是，消费者为该运营商的客户，所以，一般来说，每个推荐者能够发展多少个校园网用户是有上限的，这个上限就是该推荐者所有发生在该运营商网络内部的社交关系。如果一名推荐者的小网占比很高，就说明该推荐者可被推荐的社会关系网络中的绝大部分已经加入了校园网，因此，该推荐者没有更多的被推荐对象，所以推测他能为企业带来的价值也许不高。

3.部署环境

3.1 导入依赖库

包括数据处理模块、机器学习模块、统计分析模块等等。

import numpy as np
import pandas as pd
import statsmodels.api as sm
from scipy import stats
from itertools import combinations
from sklearn.cluster import KMeans  # K均值聚类
from pandas.plotting import lag_plot,autocorrelation_plot  # 滞后残差图、自相关系数折线图
from statsmodels.stats.diagnostic import acorr_breusch_godfrey #序列自相关拉格朗日乘数检验(BG检验、LM检验)
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf #自相关图、偏自相关图
from sklearn.preprocessing import StandardScaler  # 数据标准化
from IPython.core.display_functions import display

3.2 设置可视化

主要针对数据可视化部分，进行全局样式变量进行配置。

import seaborn as sns
sns.set_style('white')  # 当出现pycharm风格错乱时，可使用此语句修正
from matplotlib import pyplot as plt
plt.rcParams['xtick.bottom']=True  # 设置横轴刻度线可见
plt.rcParams['ytick.left']=True  # 设置纵轴刻度线可见
plt.rcParams['figure.autolayout']=True  #自动tight布局，解决多个plots出现重叠问题
plt.rcParams['axes.unicode_minus']=False  # 解决负号显示问题
plt.rcParams['font.sans-serif']=['Microsoft YaHei']  # 解决中文显示问题
plt.rcParams['figure.dpi']=80  # 设备图形分辨率
%matplotlib inline

3.3定义函数

绘制分组箱线图。

def grouping_boxplot(grouping_variable,
                grouping_variable_label,
                     box_variable,
                     box_variable_label,data
                    ):
# 绘制分组箱线图
    boxplot_data=[data[data[grouping_variable]==value][box_variable].dropna() 
                  for value in data[grouping_variable].value_counts().index]  # 构造用于制作箱形图的数据
    plt.boxplot(boxplot_data,  # 数据结构为列表套列表，一个列表绘制一个箱线图
                labels=data[grouping_variable].value_counts().index,  # 每个箱线图在横轴的标签
                patch_artist=False,  # 设置是否往箱体填充颜色，默认不填充(False)
                showmeans=True,  # 在箱子内标出均值所在位置，箱体内部的横线为中位数
                widths=0.5,  # 设置箱子的宽度，默认为0.5
                showfliers=False,  # 设置是否显示异常值，默认显示异常值(True)
                medianprops={'linestyle': '-', 'color': 'black'}  # 设置中位数线的类型和颜色
                )
    plt.xlabel(grouping_variable_label)
    plt.ylabel(box_variable_label)

步进法(stepwise)选择进入模型的自变量。

上下滑动查看更多源码

def stepwise_select_variable(
                x_var,
                y_var,
                pvalue_in=0.05,
                pvalue_out=0.1):
# 步进法(stepwise)选择进入模型的自变量：
# 如果p值小于pvalue_in，则往模型中放入此变量；
# 如果p值大于pvalue_out，则从模型中移出此变量
    variables_in=[]  # 用于存储模型中的变量
    while True:  # 直接设置为True，则让while永远循环，直到遇到break才跳出循环
        flag=False
    # ---------
    # 挑选p值最小且小于pvalue_in的自变量
        variables_out=list(set(x_var.columns)-set(variables_in))  
        # 用于存储未进入模型的变量，
        # 其值为矩阵x的所有变量列减去模型内的变量列（set是一个集合，无序且内容不能重复）
        pvalues=pd.Series(index=variables_out,dtype='float64')  
        # 创建一个series（索引为未进入模型的变量的名称），
        # 用于存储自变量回归系数(不含截距)的p值
        for new_column in variables_out:  # 遍历未进入模型的变量
            x_var_cons=sm.add_constant(x_var[variables_in+[new_column]])  
            # 确定自变量，并在最左边加上一列全为1的数据，使得模型矩阵中包含截距
            model_stepwise=sm.OLS(y_var,x_var_cons).fit()  
            # 用未标准化数据拟合模型：如自变量为x_var_cons，
            # 则拟合含截距模型；如自变量为x_var，则拟合不含截距模型
            pvalues[new_column]=model_stepwise.pvalues[new_column]  
            # 将刚进入模型的变量的回归系数的p值存储到pvalues列表（不含截距的p值）
        sig_pvalue=pvalues.min()  # 获取pvalues列表中的最小值
        if sig_pvaluepvalue_out:
            flag=True # 由于存在大于pvalue_out的p值，所以循环得继续，不可跳出循环，因此，设置flag为True
            notsig_variable=pvalues.index[pvalues.argmax()]  
            # 获取最大p值对应的自变量（argmax返回最大值的坐标，如遇多个最大值，
            # 则返回第1个最大值的坐标）
            variables_in.remove(notsig_variable)  
            # 将最大p值对应的自变量移出用于储存模型中的变量的variables_in列表
            # -------
            # 制作系数表格（含变量名称、非标准化回归系数、t值、p值）
            x_var_cons=sm.add_constant(x_var[variables_in])
            model_stepwise=sm.OLS(y_var,x_var_cons).fit()  
            # 用未标准化数据拟合模型：如自变量为x_var_cons，则拟合含截距模型；
            # 如自变量为x_var，则拟合不含截距模型
            print('variable out: {:10} Adj.R-squared： {:5} 方程显著性检验p值： {:5}'.format(notsig_variable,model_stepwise.rsquared_adj,model_stepwise.f_pvalue))
            coefficient=(
                pd.DataFrame({'未标准化回归系数':model_stepwise.params})
                .assign(t值=model_stepwise.tvalues)  # 增加“t值"列
                .assign(显著性=model_stepwise.pvalues)  # 增加”显著性“列
            )
            display(coefficient)
        if not flag:  # 当flag为False时（既没有需要进入模型的变量，也没有需要剔除的变量），跳出循环
            break
    return variables_in

4.数据准备

4.1原始数据导入

df=pd.read_csv('../../数据/移动通信网络的客户价值分析.csv',encoding='gbk')  
# 数据读取中文不能正确显示时，使用encoding
# 完整代码及数据集获取：@公众号：数据STUDIO 后台回复【data】
display(df)

4.2数据记录去重

if df.duplicated().sum()>0:
    display(df[df.duplicated()])  # 显示重复数据记录
    print('数据集中存在以上{}条重复数据记录，现已删除。'.format(df[df.duplicated()].shape[0]))
    df.drop_duplicates(inplace=True)  # 删除所有字段都完全重复的数据并立即生效
    display(df)
else:
    print('数据集中不存在重复数据记录，无需去重。')

数据集中不存在重复数据记录，无需去重。

5.探索分析

5.1数据的描述分析

df.describe(percentiles=(0.01,0.25,0.5,0.75,0.99)).T

结果解读：

每个变量都有1123条数据记录，不存在缺失值，未发现明显的极端值，所有字段都不存在违背业务逻辑的数据记录。

第一，就因变量“利润环比增长率”而言，无论是样本均值还是中位数，都还不错，一个是19.3%，另一个是18.7%，这显示校园网计划获得初步成功，推荐者确实为校园网带来了正的相对利润。但是，从标准差来看，差异性非常大，高达为13.2%，有的推荐者所推荐客户的利润环比增长率上升非常大，最大值达到99.3%，而有的推荐者所推荐客户的利润环比增长率下降非常大，最大跌幅高达49.8%。正是有这么大的差异，所以本研究就显得非常必要。

第二，就自变量“月通话总量”而言，推荐者推荐当月的通话总量在258分钟左右，最大值为360分钟，最小值为78分钟，显示无异常数据。

第三，就自变量“大网占比”而言，其平均值为84.6%，中位数为89.8%，说明所有推荐者都是该运营商深度套牢用户，因为他们主要通信社交圈都发生在该运营商的网络内。

第四，就自变量“小网占比”而言，其平均值为25.2%，中位数为19.8%，说明推荐者的通信社交圈为校园网覆盖的比例并不高，还有很大的发展潜力。

5.2数据的分布形态

查看数据分布情况，有助于特征工程根据数据分布选择合适的数据处理办法（包括缺失值、异常值处理，连续特征离散化），还有助于深入了解用户行为。

对于连续数据，当偏度系数等于0时，数据呈左右对称分布；当偏度系数绝对值大于等于1时，数据呈严重偏斜分布；当偏度系数绝对值大于等于0.5并且小于1时，数据呈中等偏斜分布；当偏度系数绝对值大于0并且小于0.5时，数据呈轻微偏斜分布。

对于分类数据，主要观察柱状图的左右对称性。

本数据集全为连续数据，没有分类数据。

# 偏度系数分析
skw_analysis=(
    pd.DataFrame({'偏度系数':df.skew(numeric_only=True)})  # 只计算数值型字段的偏度系数
    .assign(偏斜程度=df.skew(numeric_only=True).to_frame()[0].apply(lambda z:'严重' if abs(z)>=1 else '中等' if abs(z)>=0.5 else '轻微'))  # 新增“偏斜程度”列
    .assign(偏斜方向=df.skew(numeric_only=True).to_frame()[0].apply(lambda z:'左偏' if z<0 else '对称' if z==0 else '右偏'))  # 新增“偏斜方向”列)
    .sort_values(by='偏度系数',ascending=True)  # 按“偏度系数”变量升序排序
)
display(skw_analysis)

# 数据分布可视化
plt.figure(figsize=(16,8))
rows = 2
cols = 4
gs=plt.GridSpec(rows,cols)
for col in range(cols):
    colnames = ['利润环比增长率', '月通话总量', '大网占比', '小网占比']
    label = colnames[col] if colnames[col] != '月通话总量' else colnames[col] + '（分钟）'
    plt.subplot(gs[0,col])
    plt.hist(df[colnames[col]],edgecolor='white',bins=100)
    plt.xlabel(colnames[col] if colnames[col] != '月通话总量' else colnames[col] + '（分钟）')
    plt.ylabel('频数')
    if col == 2:
        plt.subplot(gs[1, col], sharey=plt.subplot(gs[1,3]))
    else:
        plt.subplot(gs[1, col])
    plt.boxplot(df[col], labels=label,
                showmeans=True, 
                showfliers=True)

结果解读：

• 第一，字段“大网占比”数据呈严重左偏分布，存在极小值。

• 第二，字段“小网占比”数据呈中等右偏分布，存在极大值。

• 第三，字段“月通话总量”、“利润环比增长率”数据分别呈轻微左偏、轻微右偏分布，分布形态近似对称，但是都存在极大值和极小值，后续在数据清洗时需进行处理（本次商业数据分析暂时不进行数据清洗），不然会影响模型的稳定性。

5.3数据的正态检验

检验数据是否服从正态分布的方法比较多，不同检验方法对样本量的敏感度不一样：样本量n<50时，优先使用Shapiro-Wilk检验；50≤样本量n<5000时，酌情使用W检验及K-S检验；5000≤样本量n时，建议使用K-S检验。

不过，我更推荐使用D’Agostino and Pearson omnibus normality test，因为这是一种通用和强大的正态性检验方法，其基本思想：首先，计算偏度和峰度以便在不对称和形状方面量化分布离正态分布的距离：然后，计算这些值中的每一个与正态分布的预期值之间的差异，并基于这些差异的总和，计算各P值。

stats.normaltest(df)

NormaltestResult(
statistic=array( [101.1282882 ,  66.29959736, 
                  318.22271185, 124.7065164 ]), 
    pvalue=array([1.09716321e-22, 4.01074783e-15,
                  7.92165846e-70, 8.32384597e-28]))

结果解读：

由于所有P值都小于0.05，所以都拒绝原假设，认为这4个变量都不服从正态分布。

样本数据不服从正态分布是常态，但只要其分布不存在明显的偏态或取值不存在异常值，一般无需对数据进行处理，如果一定想处理的话，一般采用取自然对数的方法进行处理。

5.4数据的相关性分析

# 绘制配对图
sns.pairplot(df)  
#sns.pairplot(df,
              x_vars=['月通话总量','大网占比','小网占比'],
              y_vars='利润环比增长率',height=4,aspect=1)

# 计算pearson相关系数
df.corr(method='pearson')

结果解读：

• 第一，配对图显示，利润环比增长率与月通话总量存在线性相关。

• 第二，相关系数显示，利润环比增长率与月通话总量存在显著线性正相关（r=-0.7379），大网占比与小网占比存在显著负相关（r=-0.6557）。

5.5数据的箱线图分析

由于本案例的4个变量都是连续变量，因此，优先选择散点图来尝试探索变量间的大概关系(正相关、负相关)，但是，对于大多数实际问题而言，数据噪声很大，很难从散点图上清晰地发现规律，所以，经常使用分组箱线图进行探索。

对于本案例，先将"利润环比增长率"因变量按升序排序，把其前27%的数据划为低价值组（303个样本），把其后27%的数据划为高价值组（303个样本），然后对每一个自变量做分组箱形图，分组箱形图可以直观的展示出因变量与自变量之间的关系。

df=df.assign(推荐者价值=df.利润环比增长率.map(
  lambda z:'高' if z>=df.利润环比增长率.nlargest(303).min() 
          else '低' 
         if z<=df.利润环比增长率.nsmallest(303).max() 
          else None))
                  
#df.boxplot(column=['大网占比','小网占比'],by='推荐者价值',layout=(1,3),figsize=(12,4),grid=False)  # 纵坐标的量纲需一致，否则箱子会变形，因为所有图形共享一个纵坐标
plt.figure(figsize=(12,4))
gs=plt.GridSpec(1,3)
plt.subplot(gs[0,0])
grouping_boxplot('推荐者价值','推荐者价值','月通话总量','月通话总量（分钟）',data=df)
plt.subplot(gs[0,1])
grouping_boxplot('推荐者价值','推荐者价值','大网占比','大网占比',data=df)
plt.subplot(gs[0,2],sharey=plt.subplot(gs[0,1]))  # 共享gs[0,1]的纵坐标
grouping_boxplot('推荐者价值','推荐者价值','小网占比','小网占比',data=df)

结果解读：

• 第一，高价值推荐者的月通话总量比低价值推荐者高。

• 第二，高价值推荐者的大网占比比低价值推荐者高。

• 第三，高价值推荐者的小网占比比低价值推荐者低。

6.回归分析

6.1模型构建

6.1.1无交互效应模型

1、输入法筛选自变量

x_enter=df[['月通话总量', '大网占比', '小网占比']]  # 确定自变量数据
y_enter=df.利润环比增长率  # 确定因变量数据
X_enter=sm.add_constant(x_enter)  # 加上一列全为1的数据，使得模型矩阵中包含截距
model_enter=sm.OLS(y_enter,X_enter).fit()  
    # 用未标准化数据拟合模型：
    # X大写则拟合含截距模型，
    # x小写则拟合不含截距项模型，
    # 标准化与未标准化模型的x大小写需一致，否则检验统计量取值将不一致
print(model_enter.summary())

结果解读：

自变量“小网占比”未通过显著性检验（p=0.638>0.05），最终建模时需删除“小网占比”自变量。

2、步进法筛选自变量

x_step=df[['月通话总量', '大网占比', '小网占比']]  # 确定自变量全集数据
y_step=df.利润环比增长率  # 确定因变量数据
x_step=df[stepwise_select_variable(x_step,y_step)]  # 使用步进法筛选出的自变量，stepwise_select_variable函数的功能是使用步进法筛选自变量，并返回最终筛选出的自变量名称
X_step=sm.add_constant(x_step)  # 加上一列全为1的数据，使得模型矩阵中包含截距
model_step=sm.OLS(y_step,X_step).fit()  # 用未标准化数据拟合模型：X大写则拟合含截距模型，x小写则拟合不含截距项模型，标准化与未标准化模型的x大小写需一致，否则检验统计量取值将不一致
print(model_step.summary())

variable in: 月通话总量      
Adj.R-squared：0.54414892458074 
方程显著性检验p值：1.1532634227093457e-193

variable in: 大网占比       
Adj.R-squared：0.5562037611861936 
方程显著性检验p值：9.74806646667517e-199

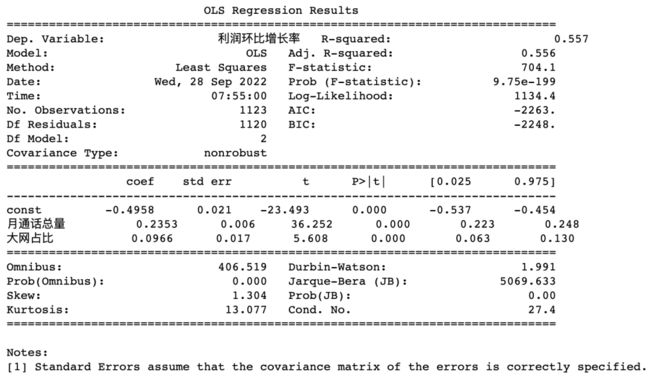
结果解读：

最终只有“月通话总量”和“大网占比”进入模型，“小网占比”被剔除出模型，和使用“输入法”选择自变量的结果一致。

3、子集法筛选自变量

x_all=df[['月通话总量', '大网占比', '小网占比']]  # 确定包含所有自变量的数据
y_all=df.利润环比增长率  # 确定因变量数据
subset_score=pd.DataFrame(columns=['independent_variable','Rsquare','Rsquare_adj','AIC','BIC'])
i=0  # 用于确定往subse_score数据集的第几行添加数据
for x_quantity in range(1,x_all.shape[1]+1):  # 确定自变量组合中自变量的数量
    for x_com in combinations(x_all.columns,x_quantity):  # 遍历自变量数量为x_quantity的各种自变量组合
        x=df[list(x_com)]
        X=sm.add_constant(x)
        model_all=sm.OLS(y_all,X).fit()
        subset_score.loc[i]=[x_com,model_all.rsquared,model_all.rsquared_adj,model_all.aic,model_all.bic]
        i+=1

通过Rsquare_adj选择自变量子集。

subset_score.loc[subset_score.Rsquare_adj.argmax(),'independent_variable'] 
# 选择rsquare_adj取值最大的子集进入最终模型，argmax返回最大值对应的索引号

('月通话总量', '大网占比')

通过AIC准则选择自变量子集。

subset_score.loc[subset_score.AIC.argmin(),'independent_variable']  
# 选择rsquare_adj取值最大的子集进入最终模型，argmax返回最大值对应的索引号

('月通话总量', '大网占比')

通过BIC准则选择自变量子集。

subset_score.loc[subset_score.BIC.argmin(),'independent_variable']  
# 选择rsquare_adj取值最大的子集进入最终模型，argmax返回最大值对应的索引号

('月通话总量', '大网占比')

结果解读：

经过对自变量的所有子集进行拟合，使用Rsquare_adj、AIC准则、BIC准则对模型进行筛选，所筛选出的自变量都是“月通话总量”和“大网占比”两个。

结论：

“输入法”、“步进法”、“子集法”等三种自变量筛选法所筛选出的自变量都是“月通话总量”和“大网占比”两个，因此，最终进入模型的自变量为“月通话问题”和“大网占比”。

6.1.2有交互效应模型

x_interact=df[['月通话总量','大网占比']].assign(月通话总量x大网占比=df.月通话总量*df.大网占比)
X_interact=sm.add_constant(x_interact)
y_interact=df.利润环比增长率
model_interact=sm.OLS(y_interact,X_interact).fit()
print(model_interact.summary())

结果解读：

由于交互项“月通话总量x大网占比”不显著（p=0.590>0.05），因此，不存在交互效应。

6.2模型诊断

6.2.1多重共线性诊断

# 计算VIF
IDV=['月通话总量','大网占比','小网占比']  # 确定自变量名称全集，IDV=independent variable
vifs=[]
for variable in IDV:
    x_vif=df[list(set(IDV)-{variable})]
    X_vif=sm.add_constant(x_vif)
    y_vif=df[variable]
    model_vif=sm.OLS(y_vif,X_vif).fit()  # 用未标准化数据拟合模型：X大写则拟合含截距模型，x小写则拟合不含截距项模型，标准化与未标准化模型的x大小写需一致，否则检验统计量取值将不一致
    vif=1/(1-model_vif.rsquared)
    vifs.append(vif)
VIFS=pd.DataFrame(index=IDV).assign(VIF=vifs).sort_values(by='VIF',ascending=False)  # 按各变量vif值降序排序
display(VIFS)

结果解读：

当VIF<5时，回归方程存在轻度多重共线性；当5≤VIF<10时，回归方程存在较严重的多重共线性；当10≤VIF时，回归方程存在严重的多重共线性。

因此，自变量之间不存在多重共线性问题。

6.2.2方差不齐性诊断

1、残差散点图法

x_hetero=df[['月通话总量', '大网占比', '小网占比']]  # 确定自变量数据
y_hetero=df.利润环比增长率  # 确定因变量数据
X_hetero=sm.add_constant(x_hetero)  # 加上一列全为1的数据，使得模型矩阵中包含截距
model_hetero=sm.OLS(y_hetero,X_hetero).fit()  # 用未标准化数据拟合模型：X大写则拟合含截距模型，x小写则拟合不含截距项模型，标准化与未标准化模型的x大小写需一致，否则检验统计量取值将不一致
df=(
    df.assign(resid=model_hetero.resid)  # 新增“resid”列，表示未标准化残差
    .assign(sdresid=model_hetero.outlier_test().student_resid)  # 新增”sdresid“列，表示学生化删除后残差(等价于model_hetero.get_influence().resid_studentized_external)
)
sns.pairplot(df,x_vars=['月通话总量','大网占比','小网占比'],y_vars=['resid','sdresid'],height=4,aspect=1)  # 绘制残差散点图

结果解读：

散点图显示，未标准化残差及学生化删除后残差与三个自变量都不存在明显的线性关系，因此，不存在方差不齐性。

2、等级相关系数法

IDV=['月通话总量','大网占比','小网占比']  # 确定自变量名称全集，IDV=independent variable
for variable in IDV:
    print('未标准化残差与“{}”变量的spearman等级相关系数为{}，p值为{}。'
          .format(variable,stats.spearmanr(abs(df.resid),df[variable])[0],stats.spearmanr(abs(df.resid),df[variable])[1]))
    print('学生化删除后残差与“{}”变量的spearman等级相关系数为{}，p值为{}。'
          .format(variable,stats.spearmanr(abs(df.sdresid),df[variable])[0],stats.spearmanr(abs(df.sdresid),df[variable])[1]))

未标准化残差与“月通话总量”变量的spearman等级相关系数为
0.031471496792663256，p值为0.2920047768383987。
学生化删除后残差与“月通话总量”变量的spearman等级相关系数为
0.031522051641127945，p值为0.29122989772460245。
未标准化残差与“大网占比”变量的spearman等级相关系数为
-0.004794315991555318，p值为0.8724988457644585。
学生化删除后残差与“大网占比”变量的spearman等级相关系数为
-0.0049131032889456515，p值为0.8693677868252431。
未标准化残差与“小网占比”变量的spearman等级相关系数为
0.01220849987834211，p值为0.6827737839962207。
学生化删除后残差与“小网占比”变量的spearman等级相关系数为
0.012965747385529707，p值为0.6642651943572604。

结果解读：

未标准化残差、学生化删除后残差与三个自变量的spearman等级相关系数均不显著（p值都大于0.05），因此，认为不存在方差不齐性。

3、BP检验

sm.stats.diagnostic.het_breuschpagan(model_hetero.resid,exog_het=model_hetero.model.exog)

(3.4984809632531215, 0.32095918822451, 
 1.1656378996396506, 0.3216685113072825)

结果解读：

第一个值是LM统计量，第二个值是LM统计量对应的p值，结果说明接受残差方差为常数的原假设（p>0.05）；第三个值是F统计量，用于检验残差平方与自变量之间是否独立，如果独立则说明残差方差齐性，第四个值为F统计量对应的p值，说明残差项满足方差齐性（p>0.05）。

6.2.3序列相关性诊断

1、自相关系数和偏自相关系数

x_autocorr=df[['月通话总量', '大网占比', '小网占比']]  # 确定自变量数据
y_autocorr=df.利润环比增长率  # 确定因变量数据
X_autocorr=sm.add_constant(x_autocorr)  # 加上一列全为1的数据，使得模型矩阵中包含截距
model_autocorr=sm.OLS(y_autocorr,X_autocorr).fit()  # 用未标准化数据拟合模型：X大写则拟合含截距模型，x小写则拟合不含截距项模型，标准化与未标准化模型的x大小写需一致，否则检验统计量取值将不一致
# 计算自相关系数和偏自相关系数
pd.DataFrame({'自相关系数':sm.tsa.stattools.acf(model_autocorr.resid,nlags=20),
              '偏自相关系数':sm.tsa.stattools.pacf(model_autocorr.resid,nlags=20,method='ywm')})  # 采用Yule-Walker方法，结果与SPSS结果一致

上下滑动查看更多

# 绘制自相关系数折线图
plt.figure(figsize=(12,4))
autocorrelation_plot(model_autocorr.resid)
plt.xticks(list(range(23)))
plt.title('自相关系数折线图')
plt.xlabel('滞后阶数')
plt.ylabel('自相关系数')

结果解读：

自相关系数的取值区间为[-0.059~0.079]，都非常小，故认为不存在序列相关性。

# 绘制自相关图和偏自相关图
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(16,5),dpi=80)
plot_acf(model_autocorr.resid,ax=axes[0],lags=20)  # 绘制自相关图
axes[0].set_title('自相关图')  # 设置自相关图标题，也可不设置，采用默认值Autocorrelation
axes[0].set_ylabel('自相关系数')
axes[0].set_xlabel('滞后阶数')
axes[0].set_xticks(list(range(21)))

plot_pacf(model_autocorr.resid,lags=20,ax=axes[1],method='ywm')  # 采用Yule-Walker方法，结果与SPSS结果一致
axes[1].set_title('偏自相关图') #设置偏自相关图标题，也可不设置，采用默认值Partial Autocorrelation
axes[1].set_ylabel('偏自相关系数')
axes[1].set_xlabel('滞后阶数')
axes[1].set_xticks(list(range(21)))

结果解读：

自相关图和偏自相关图，反映了残差序列的各阶自相关系数的大小，该图的高度值对应的是各阶自相关系数的值，蓝色区域是95%置信区间，这两条界线是检测自相关系数是否为0时所使用的判别标准：当代表自相关系数的柱条超过这两条界线时，可以认定自相关系数显著不为0。

观察上图可知，基本上所有的点都落在95%置信区间内，所以初步判断不存在序列相关性。

2、滞后残差散点图

# 绘制t期残差与其滞后1-4阶的图
def draw_resid():
    plt.figure(figsize=(16,8))
    n, rows, cols = 0, 2, 4
    gs=plt.GridSpec(rows,cols)
    for row in range(rows):
        for col in range(cols):
            n += 1
            plt.subplot(gs[row,col])
            lag_plot(model_autocorr.resid,lag=n)  # lag表示滞后期数
            
draw_resid()

结果解读：

由图可知，散点未呈现任何线性关系，故认为不存在序列相关性。

3、残差时序图

plt.scatter(df.index,model_autocorr.resid)
plt.xlabel('索引号')
plt.ylabel('残差')

结果解读：

由图可知，散点未呈现任何规律性，故认为不存在序列相关性。

4、Durbin-Watson检验

print('Durbin-Watson值为{}。'.format(sm.stats.stattools.durbin_watson(model_autocorr.resid))) 
# 计算Durbin-Watson值

Durbin-Watson值为1.9906362533785131。

结果解读：

样本量太多，无法查寻DW检验表，故无法通过DW值判断序列相关性，需使用LM检验。不过，由于DW值趋近于2，根据自相关系数的计算公式，可知自相关系数趋近于0，认为不存在序列相关性（一阶）。

5、拉格朗日乘数检验(又称为LM检验、BG检验)

Davidson and MacKinnon(1993)建议，把残差中因滞后而缺失的项用其期望值0来代替，以保持样本容量为n。acorr_breusch_godfrey函数采用的是Davidson-MacKinnon方法。

acorr_breusch_godfrey函数的重要参数：

• res：回归结果，对该模型的残差进行自相关检验，此处应当填写模型名称（如model_autocorr）

• nlags：滞后阶数

acorr_breusch_godfrey函数的返回结果：

• lm_statistic：LM统计量值

• lm_pvalue：LM统计量的p值，若p值小于显著性水平，则拒绝无自相关性的原假设，即存在自相关性

• f_statistic：F统计量值（resid_lag1、resid_lag2、resid_lag3、……、resid_lagk联合显著的F检验统计量）

• f_pvalue：F统计量对应的p值，若p值小于显著性水平，则拒绝无自相关性的原假设，即存在自相关性

bg_result=acorr_breusch_godfrey(model_autocorr,nlags=20)  # 拉格朗日乘数检验，nlags为滞后阶数
bg_test_output=pd.Series(bg_result[0:4],index=['lm_statistic','lm_pvalue','f_statistic','f_pvalue'])
display(bg_test_output)

lm_statistic    24.898569
lm_pvalue        0.205339
f_statistic      1.245947
f_pvalue         0.207554
dtype: float64

结果解读：

两个检验的p值都大于0.05，故认为不存在序列相关性。

6.3模型结果

6.3.1非标准化回归模型

由于：

• 第一，根据“输入法”、“步进法”、“子集法”自变量筛选方法的分析结论，可知最终模型只包括”月通话总量“和”大网占比“两个自变量。

• 第二，根据模型的多重共线性、方差齐次性、序列相关性诊断结论，可知模型不存在多重共线性、方差齐次性、序列相关性等问题。

因此：

在最终的回归模型当中，只纳入”月通话总量“和”大网占比“两个自变量，剔除“小网占比”自变量。

x_end_variables=['月通话总量','大网占比']  # 确定最终进入模型的自变量的名称
#y_end_variable=['利润环比增长率']  # 确定最终进入模型的因变量的名称
x_end=df[x_end_variables]  # 确定最终进入模型的自变量数据
y_end=df['利润环比增长率']  # 确定最终进入模型的因变量数据
scaler=StandardScaler()  # 建模：创建数据标准化模型
x_end_std=scaler.fit_transform(x_end)  
    # 标准化x：fit-用数据训练模型；
    # transform-用训练好的模型对数据进行转换；
    # fit_transform-用数据训练模型，并用训练好的模型对数据进行转换（二合一）
y_end_std=scaler.fit_transform(np.array(y_end).reshape(-1,1))  # 标准化y
X_end=sm.add_constant(x_end)  # 加上一列全为1的数据，使得模型矩阵中包含截距
X_end_std=sm.add_constant(x_end_std)  # 加上一列全为1的数据，使得模型矩阵中包含截距
model_end=sm.OLS(y_end,X_end).fit()  
    # 用未标准化数据拟合模型：
    # X大写则拟合含截距模型，
    # x小写则拟合不含截距项模型，
    # 标准化与未标准化模型的x大小写需一致，否则检验统计量取值将不一致
model_end_std=sm.OLS(y_end_std,X_end_std).fit()  
    # 用标准化数据拟合模型：
    # X大写则拟合含截距模型，
    # x小写则拟合不含截距项模型，
    # 标准化与未标准化模型的x大小写需一致，否则检验统计量取值将不一致
print(model_end.summary())  # 非标准化回归模型摘要

6.3.2标准化回归模型

print(model_end_std.summary())  # 标准化回归模型摘要

6.3.3结果呈现表格

# 绘制结果呈现表格
pd.DataFrame({'coef':round(model_end.params,4),
              'Std.Error':round(model_end.bse,4),
              'tvalue':round(model_end.tvalues,3),
              'pvalue':round(model_end.pvalues,3),
              'lower 95% CI':round(model_end.conf_int(0.05)[0],3),
              'upper 95% CI':round(model_end.conf_int(0.05)[1],3),
              'std coef':model_end_std.params.round(4),
              'VIF':VIFS.loc[x_end_variables].VIF
              })

6.4模型应用

6.4.1客户群体细分

根据模型结果，最有价值的推荐者应具备两个特征：第一，月通话总量高，这意味着推荐者是个“话痨”；第二，大网占比高，这意味着推荐者的主要移动通信社交圈都发生在该运营商的网络内。

对于这两个特征，使用聚类分析法将“月通话总量”变量分为“高”和“低”两类，将“大网占比”变量也分为“高”和“低”两类，于是便将客户群细分为4类：第一类，高月通话总量、高大网占比；第二类，高月通话总量、低大网占比；第三类，低月通话总量、高大网占比；第四类，低月通话总量、低大网占比。

1、单变量细分

KMeans算法的基本原理

KMeans算法名称中的K代表类别数量，Means代表每个类别内样本的均值，所以KMeans算法又称为K-均值算法。KMeans算法以距离作为样本间相似度的度量标准，将距离相近的样本分配至同一个类别。样本间距离的计算方式可以是欧氏距离、曼哈顿距离、余弦相似度等，KMeans算法通常采用欧氏距离来度量各样本间的距离。

KMeans算法的核心思想是对每个样本点计算到各个中心点的距离，并将该样本点分配给距离最近的中心点代表的类别，一次迭代完成后，根据聚类结果更新每个类别的中心点，然后重复之前操作再次迭代，直到前后两次分类结果没有差别。

基本操作步骤：

• 步骤1：随机选择K个中心点。

• 步骤2：依据欧氏距离度量相似度，将每个样本点都分配给最近的中心点。

• 步骤3：根据聚类结果，更新每个类别的中心点。

• 步骤4：重复步骤2，将每个样本点重新分配给距离最近的中心点。

• 步骤5：重复步骤3，更新中心点。

• 步骤6：重复步骤4，判断聚类结果是否与上次结果一致，若一致则算法终止，否则回到步骤5。

kms=KMeans(n_clusters=2,random_state=20220923)  
# 建模：设置模型参数：n_clusters表示将样本聚为2类；
    # random_state设置种子参数，使得每次运行代码时选取的初始中心点都一样。
    # 增加”月通话总量分类“和”大网占比分类“新列
df['月通话总量分类']=kms.fit(np.array(df.月通话总量).reshape(-1,1)).labels_  
# 拟合：用数据拟合（训练）刚刚所建模型，labels_属性返回聚类结果
df['大网占比分类']=kms.fit(np.array(df.大网占比).reshape(-1,1)).labels_  
# 拟合：用数据拟合（训练）刚刚所建模型，labels_属性返回聚类结果
display(df)

# 确定分类代码的业务含义
print(df.groupby('月通话总量分类').月通话总量.mean())
print(df.groupby('大网占比分类').大网占比.mean())

月通话总量分类
0    2.888206
1    2.259800
Name: 月通话总量, dtype: float64
大网占比分类
0    0.615438
1    0.915795
Name: 大网占比, dtype: float64

结果解读：

• 第一，在对”月通话总量“变量进行分类时，0代表”高“，1代表”低“。

• 第二，在对”大网占比“变量进行分类时，0代表”低“，1代表”高“。

# 把数字0和1换成具有业务含义的”高“和”低“
df.月通话总量分类.replace([0,1],['高','低'],inplace=True)
df.大网占比分类.replace([0,1],['低','高'],inplace=True)

2、双变量细分

# 计算各类的数量
crosstab_quantity=pd.crosstab(df.大网占比分类,df.月通话总量分类)
display(crosstab_quantity)

# 计算各类的占比
crosstab_percent=pd.crosstab(df.大网占比分类,df.月通话总量分类,normalize=True)
display(crosstab_percent)

# 绘制客户群体细分表
crosstab=pd.DataFrame(index=['大网占比_低','大网占比_高'],columns=['月通话总量_低','月通话总量_高'])
crosstab.iloc[0,0]='{}({:.2%})[D.最劣质客户-放弃]'.format(crosstab_quantity.iloc[0,0],crosstab_percent.iloc[0,0])
crosstab.iloc[0,1]='{}({:.2%})[C.高潜力客户-策反]'.format(crosstab_quantity.iloc[0,1],crosstab_percent.iloc[0,1])
crosstab.iloc[1,0]='{}({:.2%})[B.待激活客户-激活]'.format(crosstab_quantity.iloc[1,0],crosstab_percent.iloc[1,0])
crosstab.iloc[1,1]='{}({:.2%})[A.高价值客户-套牢]'.format(crosstab_quantity.iloc[1,1],crosstab_percent.iloc[1,1])
display(crosstab)

plt.scatter(df[(df.大网占比分类=='高')&(df.月通话总量分类=='高')].大网占比,
            df[(df.大网占比分类=='高')&(df.月通话总量分类=='高')].月通话总量,
            label='高价值客户',c='blue',marker='o')
plt.scatter(df[(df.大网占比分类=='低')&(df.月通话总量分类=='低')].大网占比,
            df[(df.大网占比分类=='低')&(df.月通话总量分类=='低')].月通话总量,
            label='最劣质客户',c='red',marker='^')
plt.scatter(df[(df.大网占比分类=='高')&(df.月通话总量分类=='低')].大网占比,
            df[(df.大网占比分类=='高')&(df.月通话总量分类=='低')].月通话总量,
            label='待激活客户',c='black',marker='*')
plt.scatter(df[(df.大网占比分类=='低')&(df.月通话总量分类=='高')].大网占比,
            df[(df.大网占比分类=='低')&(df.月通话总量分类=='高')].月通话总量,
            label='高潜力客户',c='green',marker='x')
plt.xlabel('大网占比')
plt.ylabel('月通话总量（百分钟）')
plt.legend()

6.4.2营销策略建议

根据前面的模型分析结果可知，最有价值的推荐者应当具备两个特征：第一，月通话总量高，这意味着推荐者是个话痨；第二，大网占比高，这意味着推荐者的主要通信社交圈都发生在该运营商的网络内。

基于这两个特征，运用K均值聚类分析法，将自变量”月通话总量“、”大网占比“分别分成2组，并构建客户群体细分表，于是，就把推荐者分成4类，对每类推荐者，我们可以制定针对类营销策略。

对于群体A，对应的是最优质的高价值客户，占样本比为40.52%，其特征是高通话量、高大网占比。因此，对这部分客户的营销策略是向其提供最优质的营销资源和最好的客户服务，将他们深度的套牢，同时，还应当向他们提供最激进的奖励机制，鼓励他们将大网中的好友发展为校园网用户。

对于群体B，对应的是待激活客户，占样本比为36.15%，其特征是低通话总量、高大网占比。这部分客户的优势是大网占比高，这说明他们的通信社交圈被同一个运营商大量覆盖，他们的的劣势是通话总量不高，活跃度低。如果通过合理的营销策略刺激他们提高通话量，有可能其通话对象的通话量也会被大大提高。

对于群体C，对应的是高法力客户，占样本10.95%，其特征是高通话总量、低大网占比。这部分客户的优势是通话量高，活跃度高，劣势是大网占比低。这说明他们有大量高价值通信对象未被该运营商覆盖。因此，可考虑为这批客户设立激进的推荐奖励机制，鼓励他对身边好友进行策反，邀请他身边好友加入该运营商，以提高大网占比。

对于群体D，对应的是最劣质客户，占样本12.38%，其特征是低通话总量、低大网占比。他们既不活跃，又有大量的通信对象未被该运营商覆盖，是最劣质的一批用户，在营销资源有限的情况下，他们或许可以被暂时放弃。

- END -

对比Excel系列图书累积销量达15w册，让你轻松掌握数据分析技能，可以点击下方链接进行了解选购：