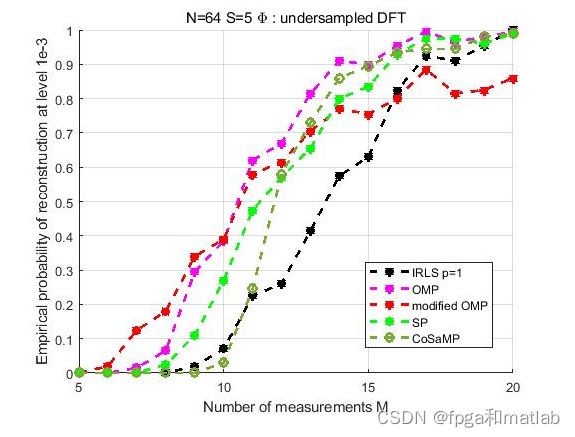
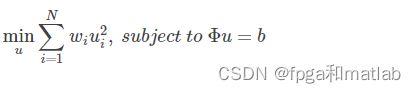对比IRLS,OMP,MOMP,SP以及CoSaMP五种压缩感知算法的信号重构性能

UP目录

一、理论基础

1.1IRLS

1.2OMP

1.3SP

1.4CoSaMP

二、核心程序

三、测试结果

---

一、理论基础

        压缩采样匹配追踪(CompressiveSampling MP)是D. Needell继ROMP之后提出的又一个具有较大影响力的重构算法。CoSaMP也是对OMP的一种改进，每次迭代选择多个原子，除了原子的选择标准之外，它有一点不同于ROMP：ROMP每次迭代已经选择的原子会一直保留，而CoSaMP每次迭代选择的原子在下次迭代中可能会被抛弃。

        压缩感知（Compressed sensing），也被称为压缩采样（Compressive sampling）或稀疏采样（Sparse sampling），是一种寻找欠定线性系统的稀疏解的技术。压缩感知被应用于电子工程尤其是信号处理中，用于获取和重构稀疏或可压缩的信号。这个方法利用讯号稀疏的特性，相较于奈奎斯特理论，得以从较少的测量值还原出原来整个欲得知的讯号。核磁共振就是一个可能使用此方法的应用。这一方法至少已经存在了四十年，由于David Donoho、Emmanuel Candès和陶哲轩的工作，最近这个领域有了长足的发展。压缩感知（Compressed sensing），也被称为压缩采样(Compressive sampling)，稀疏采样(Sparse sampling)，压缩传感 [1]  。它作为一个新的采样理论，它通过开发信号的稀疏特性，在远小于Nyquist 采样率的条件下，用随机采样获取信号的离散样本，然后通过非线性重建算法完美的重建信号 [1]  。压缩感知理论一经提出，就引起学术界和工业界的广泛关注。他在信息论、图像处理、地球科学、光学/微波成像、模式识别、无线通信、生物医学工程等领域受到高度关注，并被美国科技评论评为2007年度十大科技进展。

1.1IRLS

        IRLS（iteratively reweighted least squares）算法是压缩感知重建算法当中的一个基本算法。主要是为了解决: 

本文采用的代码是加入权重之后的

上式中的权重 wiwi是根据前面一次 ui−1ui−1计算得到的，具体的计算公式为：

这样上面的最优化问题可以求解得到： 

1.2OMP

        OMP算法的改进之处在于：在分解的每一步对所选择的全部原子进行正交化处理，这使得在精度要求相同的情况下，OMP算法的收敛速度更快。那么在每一步中如何对所选择的全部原子进行正交化处理呢？在正式描述OMP算法前，先看一点基础思想。先看一个 k  阶模型，表示信号 f 经过 k 步分解后的情况，似乎很眼熟，但要注意它与MP算法不同之处，它的残值与前面每个分量正交，这就是为什么这个算法多了一个正交的原因，MP中仅与最近选出的的那一项正交。

1.3SP

        压缩采样匹配追踪(CoSaMP)与子空间追踪（SP）几乎完全一样，因此算法流程也基本一致。SP与CoSaMP主要区别在于"Ineach iteration, in the SP algorithm, only K new candidates are added, while theCoSAMP algorithm adds 2K vectors."，即SP每次选择K个原子，而CoSaMP则选择2K个原子；这样带来的好处是"This makes the SP algorithm computationally moreefficient,"。

       这个算法流程的初始化(Initialization)其实就是类似于CoSaMP的第1次迭代，注意第(1)步中选择了K个原子："K indices corresponding to the largest magnitude entries"，在CoSaMP里这里要选择2K个最大的原子，后面的其它流程都一样。这里第(5)步增加了一个停止迭代的条件：当残差经过迭代后却变大了的时候就停止迭代。 

1.4CoSaMP

       压缩采样匹配追踪(CompressiveSampling MP)是D. Needell继ROMP之后提出的又一个具有较大影响力的重构算法。CoSaMP也是对OMP的一种改进，每次迭代选择多个原子，除了原子的选择标准之外，它有一点不同于ROMP：ROMP每次迭代已经选择的原子会一直保留，而CoSaMP每次迭代选择的原子在下次迭代中可能会被抛弃。

二、核心程序

.......................................................

S=5;
% m is the number of measurement
%m=20;
A=5:20;
D=zeros(size(A));
D2=D;
Dmod=D;
D1=D;
%Dp5=D;
Dmod3=D;
Dco=D;
%Monte Carlo
Dsp=D; 

for t=1:200
    rng(t);
    for k=1:length(D)
        m                  = A(k); 
        [t,k]
        r2                 = randperm(l*c);r2=r2(1:S);rr2=r2(:);
        u_true             = zeros(l*c,1); u_true(r2)=u_true(r2)+rand(S,1);  

        phi                = (kron((fft(eye(c))).',fft(eye(l))));
        r                  = randperm(l*c);r=r(1:m);
        phi                = phi(r,:); 

        b                  = phi * u_true(:); 

       [d1,u_new1]         = IRLSregcomp(phi,b,1,u_true(:));
       [uestOMP,d2]        = OMP(phi,b,u_true,S);
       [uestOMPmod3,dmod3] = OMPmod3(phi,b,u_true,S);
       [uestco,dco]        = cosamp2(phi,b,u_true,S);
       [uestsp,dsp]        = SPA(phi,S,b,u_true);

       Dsp(k)=Dsp(k)+dsp;
       Dco(k)=Dco(k)+dco;

       Dmod3(k)=Dmod3(k)+dmod3;
       D2(k)=D2(k)+d2;
       D1(k)=D1(k)+d1; 
    end
end;

 
D1=D1/t;
Dco=Dco/t;
Dsp=Dsp/t;
Dmod=Dmod/t;
Dmod3=Dmod3/t;
D2=D2/t;
figure(1)
hold off

hold on

plot(A,D1,'k*--','LineWidth',2)
plot(A,D2,'m*--','LineWidth',2)
plot(A,Dmod3,'r*--','LineWidth',2)
plot(A,Dsp,'g*--','LineWidth',2)
plot(A,Dco,'o--','LineWidth',2)
legend('IRLS p=1','OMP','modified OMP','SP','CoSaMP')
grid
xlabel('Number of measurements M')
ylabel('Empirical probability of reconstruction at level 1e-3')
title('N=64 S=5 \Phi : undersampled DFT')
UP104

三、测试结果

在matlab2021a中仿真得到如下的效果：