论文阅读 (五)：Eigenvector centrality of nodes in multiplex networks.

引入

  论文地址

摘要

  将特征向量中心性的概念扩展到多路复用网络，并引入了一些可量化的参数，这些参数可量化代表着多层网络系统中节点的重要性，包括矢量类型中心性的定义。 此外，我们严格地表明，在合理的条件下，这种集中措施是存在的并且是独特的。 计算机实验和仿真表明，所提出的措施在应用于相同的多路复用结构时可提供实质上不同的结果，并突出介绍了引入的不同中心性措施之间的非平凡关系。
  许多生物，社会和技术系统都可以找到适合作为复杂网络的表示形式，其中节点代表系统的组成部分，而边沿则说明它们之间的相互作用。通常，节点的交互比简单的链接需要更准确的映射，因为系统的组成部分通常以多种方式同时连接。例如，在社交网络中，可以考虑几种类型的不同参与者的关系：友谊，邻居，亲戚，同一文化社会的成员身份，伙伴关系或同事关系等。在这种情况下，赋予我们的网络以互惠感多重网络结构。这种表示法反映了节点通过多层链路的交互，而传统的单层网络表示法无法捕获。社会学家长期以来一直在考虑这种多路复用表示法，尽管最近已经提出了有关多路复用网络建模和结构的，一些结果，但是在这种网络中对中​​心性参数的研究还没有。还没有得到令人满意的解决。本文的目的是提出复用网络中的中心性定义，并举例说明潜在的应用。

符号系统

   $\mathcal{G}=\{{\mathbf{G}}_1,\cdots ,{\mathbf{G}}_{\mathbf{m}}\}$ 表示一个复杂网络结构，${\mathbf{G}}_{\mathbf{k}}=(X,E_k)$ 表示第 $i$个网络层，$X=(e_1,\cdots ,e_n)$ 表示节点的集合，$E_k$ 就是边的集合，每个网络 $G_k$ 用一个邻接矩阵 $A_k=(a_{ij}^k)$ 来表示，其中
$$a_{ij}^k=\{\begin{array}{ll}1& if(e_j,e_i)\in E_k,\\ 0& otherwise.\end{array}$$
   于是一个 $\mathcal{G}$ 就能被看作是一个图 $\overline{G}=(X,E)$ ，$E={\bigcup }_{k=1}^m{E}_k$ 就是第 $k$个网络的一个边集合；然后 $\overline{G}$ 又能被 $\overline{A}={\overline{a}}_{ij}^k$ 表示：
$${\overline{a}}_{ij}^k=\{\begin{array}{ll}1& if{a}_{ij}^k\ne 0forsome1\le k\le m\\ 0& otherwise.\end{array}$$

1.特征向量中心的数学模型

提出问题

   在多路复用网络的情况下，要解决的中心问题是：考虑到并非所有子网都具有不同的子网（通道，社区，层…）之间的所有相互作用，该如何考虑在内？ 同样重要吗？ 实际上，必须指出，为了获得节点的中心性，必须考虑到节点的中心性（重要性，影响…）如何通过不同的渠道在整个网络中传播（ 层）不一定是添加剂。 例如，全球社交网络（例如Facebook或Twitter）的特征是非常不同的2种交互，这也是气候系统，博弈论和基础设施交互等领域中各个单位之间交互的典型特征。总之一句话，就是怎么找到节点的中心性。

解决问题

  参考网络 $\mathcal{G}$，对于每一层，可以将经典特征向量中心点 $G_k$ 视为 $A_k$ 的主要特征向量（如果存在）。 具体而言，层 $G_k$ 中节点 $e_i$ 的特征向量中心点将是与矩阵 $A_k$ 的最大特征值相对应的正定和归一化向量$c_k\in R_n$ 的第 $i$ 个条目。 以类似的方式，投影网络 $G$ 的特征向量中心将是 $A$ 的主要特征向量。对于具有正项的任何对称矩阵，Perron-Frobenius定理可以保证这些向量的存在和唯一性。有趣的是，Perron-Frobenius定理可以方便地扩展到多路复用网络，从而带来更深入的节点中心性概念。
  一旦计算完所有特征向量中心点，就可以将 $\mathcal{G}$ 的类似独立层特征向量的中心点（简称为 $\mathcal{G}$ 的独立层中心点）视为矩阵 $C=(c_1|c_2|\cdots |c_m)\in {\mathbb{R}}^{n\times m}$，$C$ 是一个列随机向量，并且 $\Vert c_k{\Vert }_1=1$ (绝对值和为1)
  节点的中心性（重要性）必须与其邻居（位于所有层上）的中心性成正比，并考虑到所有层具有相同的重要性，在图 $G_{\ell }$ 中，如果 $j$ 指向 $i$ ， 对于任意的 $i,j\in X$ $c(i)$ 正比于$c(j)$ ；
这允许将类似均匀特征向量的中心点（简称均匀中心点）定义为矩阵 $A={\sum }_{k=1}^m{A}_k$ 的正和归一化特征向量 $c\in {\mathbb{R}}^n$（如果存在）；例如，这种情况发生在社交网络中，其中不同的个人可能与其他人有不同的关系，而人们通常对衡量熟人网络的中心性感兴趣。
  再往前走，可以考虑在网络的不同层中将层与重要性（或影响）的不同级别相关联，并将这种信息包括在矩阵中以说明层之间的相互影响。 因此，为了计算特定层内节点的重要性（或影响力），还必须考虑所有其他层，因为其中某些层可能与该计算有关。 例如，考虑一个老板和他的一名雇员去同一个体育馆的情况：体育馆层中两个同伴之间的关系与办公室层内的人具有完全不同的性质，但是老板的角色 （即他的核心地位）在这种情况下甚至比他是办公室里唯一经常光顾那个体育馆的人更大。 换句话说，需要考虑各层之间的影响是异构的情况。
  为此，可以引入影响矩阵 $\mathbf{W}=(w_{ij})\in {\mathbb{R}}^{m\times m}$作为非负矩阵$W\ge 0$，以便 $w_{ij}$ 测量层 $G_j$ 对层 $G_i$ 的影响。 一旦固定了 $G$ 和 $\mathbf{W}=(w_{ij})$，就可以将每一层$G_k(1\le k\le m)$上的局部本征矢量样中心点（简称 $G$ 局部中心点）定义为正并归一化矩阵的特征向量 $c_k^{\ast }\in {\mathbb{R}}^n$（如果存在）
$$A_k^{\ast }=\sum _{j=1}^m{w}_{kj}{A}_j$$
再一次，将复用网络 $\mathcal{G}$ 的局部异质本征向量中心性（简称为局部异质中心性）矩阵定义为
$$C^{\ast }=(c_1^{\ast }|c_2^{\ast }|\cdots |c_m^{\ast })\in {\mathbb{R}}^{n\times m}$$
  要阐明的另一个重要方面是，通常，特定层 $k$ 中节点 $e_i$ 的中心性不仅取决于在层 $k$ 中链接到 $e_i$ 的邻居，还取决于 $e_i$ 的所有其他邻居到其他层。 在不同知识领域的科学引证就是这种情况； 的确，可以想象有两位科学家（化学家和物理学家），其中一位被授予诺贝尔奖：即使诺贝尔奖获得者在其他研究人员领域很少被引用，另一位科学家的重要性也会大大提高。 这种启发式的论证导致引入了另一个中心性概念：给定一个多重网络 $\mathcal{G}$ 和一个影响矩阵 $W=(w_{i}j)$，$\mathcal{G}$ 的全局异构特征向量样中心性（简称 $\mathcal{G}$ 的全局中心性）被定义为一个正数。 矩阵的归一化特征向量 $c^{\otimes }\in {\mathbb{R}}^{nm}$（如果存在）
$$A^{\otimes }=\left(\begin{array}{cccc}{w}_{11}{A}_1& w_{12}{A}_2& \cdots & w_{1m}{A}_m\\ w_{11}{A}_1& w_{22}{A}_2& \cdots & w_{2m}{A}_m\\ ⋮& ⋮& \ddots & ⋮\\ w_{m1}{A}_1& w_{m2}{A}_2& \cdots & w_{mm}{A}_m\end{array}\right)\in {\mathbb{R}}^{(nm)\times (nm)}$$
$A^{\otimes }$是矩阵的Khatri-Rao乘积;
$$W=\left(\begin{array}{ccc}{w}_{11}& \cdots & w_{1m}\\ ⋮& \ddots & ⋮\\ w_{m1}& \cdots & w_{mm}\end{array}\right)\text{ and }\left(A_1\left|A_2\right|\cdots \mid A_m\right)$$
  与之前类似，如果引入符号 $$c^{\otimes }=\left(\frac{\frac{c_1^{\otimes }}{c_2^{\otimes }}}{\frac{⋮}{c_m^{\otimes }}}\right),$$
  且$c_1^{\otimes },\cdots ,c_m^{\otimes }\in {\mathbb{R}}^{n\times m}$，则可以将$\mathcal{G}$的全局异质本征中心矩阵定义为$C^{\otimes }=(c_1^{\otimes },\cdots ,c_m^{\otimes })\in {\mathbb{R}}^{n\times m}$给定的矩阵，不管 $c^{\otimes }$ 是列向量还是行向量，他们每一向量的和都为1
  还要注意，矩阵$A^{\otimes }$ 可以解释为从张量积 ${\mathbb{R}}^n\otimes {\mathbb{R}}^m$ 到其自身的线性算符，其形式为 $c^{\otimes }$ 是其归一化的主特征向量。

2. 存在与一致性

(由于退出的时候没有保存，这一小节就简单的说下三个定理。。。。)

Theorem1
  如果一个多重网络 $\mathcal{G}$ 的投影图 $\overline{G}$ 是强连通的，则 $\mathcal{G}$的统一中心点 $\tilde{C}$ 存在并且是唯一的。
Theorem2
  如果多路复用网络$\mathcal{G}$ 的投影图$\overline{G}$ 强连通且 $W>0$，则$\mathcal{G}$ 的局部 $C^{\ast }$ 异构中心存在并且是唯一的。
Theorem2
  如果一个多重网络$\mathcal{G}$ 的投影图$\overline{G}$ 是强连通的，且$W>0$，则$\mathcal{G}$ 的全局异构中心 $C^{\otimes }$ 存在并且是唯一的。

3. 比较多重网络的中心

  在接下来的两节中，我们将计算和比较我们为一些示例定义的不同类型的集中度度量，这些度量基于真实数据和综合数据。我们将从描述两种比较集中度度量的方式开始，然后将它们应用于社会多元化网络的真实示例。
  如果我们使用一个由n个节点 $\{e_1,\cdots ,e_n\}$ 组成的网络，并考虑两个中心度度量$c，c^{\prime }\in {\mathbb{R}}^n$，使得$c$ 和$c^{\prime }$ 的第i个坐标测度节点$v_i$,$1\le i\le n$，一种测量$c$ 和$c^{\prime }$ 之间的相关性的方法是通过对某个范数$\Vert \cdot \Vert$ 计算$\Vert c-c^{\prime }\Vert$ 。虽然$\Vert c-c^{\prime }\Vert$ 度量了$c$ 和$c^{\prime }$ 之间的差异，但其值并不代表有关$c$ 和$c^{\prime }$ 之间的相关性的真实信息。实际上，请注意，中心度度量的主要特征之一是它们产生排名，即，在许多情况下，从中心度度量获得的关键信息是一个节点$v_i$ 比另一个节点$v_j$ 更相关的事实，并且该排序比节点$v_i$和$v_j$ 的相应中心点之间的实际差值更重要。因此，如果要分析一组中心度度量之间的相关性，则应详细研究相关排名之间的相关性。
  文献提出了各种替代方法来研究两个等级r和r’之间的相关性，两个标准方法是Spearman等级相关系数 $\rho (r，r^{\prime })$ 和Kendall等级相关系数 $\tau (r，r^{\prime })$。 如果我们考虑具有节点$\{e_1,\cdots ,e_n\}$的网络的两个中心度$c，c^{\prime }\in {\mathbb{R}}^n$，则每个中心度$c$ 和$c^{\prime }$ 都会产生一个节点等级，将由$r$ 和$r^{\prime }$ 表示 分别。

3.1 Spearman等级相关系数 $\rho (r，r^{\prime })$

  两个中心度量c和c’之间的Spearman秩相关系数定义为:
$$\rho \left(c,c^{\prime }\right)=\rho \left(r,r^{\prime }\right)=\frac{{\sum }_{i=1}^n\left(r\left(v_i\right)-\bar{r}\right)\left(r^{\prime }\left(v_i\right)-\overline{r^{\prime }}\right)}{\sqrt{{\sum }_{i=1}^n{\left(r\left(v_i\right)-\bar{r}\right)}^2{\left(r^{\prime }\left(v_i\right)-\overline{r^{\prime }}\right)}^2}}$$
其中$r(v_i)$和$r^{\prime }(v_i)$分别是节点vi相对于中心度$c$ 和$c^{\prime }$ 的等级，$\bar{r}=\frac{1}{n}{\sum }_{i}r\left(v_i\right)$ and $\overline{r^{\prime }}=\frac{1}{n}{\sum }_i{r}^{\prime }\left(v_i\right)$

3.2 Kendall等级相关系数 $\tau (r，r^{\prime })$

  两个中心度测度$c$ 和$c^{\prime }$ 之间的Kendall等级相关系数被定义为:
$$\tau \left(c,c^{\prime }\right)=\tau \left(r,r^{\prime }\right)=\frac{\tilde{K}\left(r,r^{\prime }\right)-K\left(r,r^{\prime }\right)}{\left(\begin{array}{l}n\\ 2\end{array}\right)}$$
其中$\tilde{K}(r，r^{\prime })$ 使得节点 $\{v_i，v_j\}$在 $r$ 和 $r^{\prime }$ 中以相同的顺序出现，而$K(r，r^{\prime })$以便它们在排名 $r$ 和 $r^{\prime }$ 中以不同的顺序出现。 注意，$\rho (c，c^{\prime })$ 和 $\tau (c，c^{\prime })$ 都给出[-1，1]中的值。，$\rho (c，c^{\prime })$ 越接近1，则c和c’的相关性越强，而，$\rho (c，c^{\prime })$ 越接近0，则c和c’的独立性越强（并且类似地对于 $\tau (c，c^{\prime })$ ）。 另外，如果，$\rho (c，c^{\prime })$ （或 $\tau (c，c^{\prime })$ ）接近-1，则c和c’是反相关的。

  进一步的评论来自这样一个事实，即迄今为止引入的集中度度量彼此非常不同，因此必须仔细描述如何比较它们。的确，一方面，第二节介绍的一些标量度量（网络中节点的中心）将单个数字与网络的每个节点相关联，而另一方面，其他矢量度量则将矢量分配给每个节点vi （向量的每个坐标都作为多路复用网络不同层的参与者，测量节点$v_i$ 的中心）。实际上，对于具有n个节点的多路复用网络 $\mathcal{G}$，两个标量中心(投影图的特征向量中心 $\overline{c}\in {\mathbb{R}}^n$，和均匀的特征向量样中心 $\tilde{c}\in {\mathbb{R}}^n$) 和三个向量中心(独立层中心 $C\in {\mathbb{R}}^{n\times m}$，提出了局部异质中心 $C^{\star }\in {\mathbb{R}}^{n\times m}$，以及全局异质中心 $C^{\otimes }\in {\mathbb{R}}^{n\times m}$)。为了比较这些不同的度量，必须将每个矢量类型的中心性中包含的信息进行汇总，以将数字与每个节点相关联。

3.3 汇总信息

  汇总信息有几种替代方法，但我们使用凸组合技术作为主要标准。
  对于由n个节点和m层组成的多路复用网络G，我们可以固定一些${\lambda }_1,\cdots ，{\lambda }_m\in [0，1]$使得${\lambda }_1+\cdots +{\lambda }_m=1$并计算聚集的标量中心度
$$\begin{gathered} c=c\left({\lambda }_1,\cdots ,{\lambda }_m\right)=\sum _{j=1}^m{\lambda }_j{c}_j \\ {c}^{\star }=c^{\star }\left({\lambda }_1,\cdots ,{\lambda }_m\right)=\sum _{j=1}^m{\lambda }_j{c}_j^{\star } \end{gathered}$$
  其中 $c_j$ 是独立层中心度 $C$ 的第 $j$ 列，$c_j^{\ast }$ 是局部异质中心度 $C^{\star }$ 的第 $j$ 列。 注意，每个 ${\lambda }_j$ 的值可以理解为层$G_j$ 在多路复用网络的聚集标量中心性中的相对影响。 在我们的数字中，已选择特定值${\lambda }_1=\cdots ={\lambda }_m=1/m$，因为我们假设没有有关每一层相对相关性的额外信息，因此将它们各自的影响视为等效 。 注意 $c$ 和 $c^{\ast }$ 是归一化的，因为$C$ 和$C^{\star }$ 是列随机的。
  全局异构中心性的情况是不同的，因为 $C^{\otimes }$ 不是列随机的。 在这种情况下，由于$C^{\star }$ 的所有项的总和为1，所以取$c^{\otimes }={\sum }_{j=1}^m{c}_j^{\otimes }$就足够了。其中$c_j^{\otimes }$是全局异构中心性$C^{\otimes }$ 的第 $j$ 列。 因此，每一层 $G_j$ 的相对影响可以定义为$\Vert c_j^{\otimes }\Vert$（即，$c_j^{\otimes }$的所有坐标之和）。
  汇总所有矢量量度（并将设置统一）后，我们将讨论排名比较。 除了中心度量之间的实际相关性，我们还分析了用于定义局部异质中心 $C^{\star }$ 和全局异质中心 $C^{\otimes }$ 的矩阵$W$（在第二部分中称为影响矩阵）的影响。 由于此矩阵$W\in {\mathbb{R}}^{m\times m}$是非负的，因此我们考虑两个矩阵族 $\{W_1(q)\}$ 和 $\{W_2(q)\}$ ，$0\le q\le 1$
$$W_1(q)=\left(\begin{array}{cccc}1& q& \cdots & q\\ q& 1& \cdots & q\\ ⋮& ⋮& \ddots & ⋮\\ q& q& \cdots & 1\end{array}\right),W_2(q)=\left(\begin{array}{cccc}1& q& \cdots & q\\ q^2& 1& \cdots & q\\ ⋮& ⋮& \ddots & ⋮\\ q^2& q^2& \cdots & 1\end{array}\right)$$
  注意，虽然每个$\{W_1(q)\}$ 对应于层之间的对称影响，但是每个 $\{W_2(q)\}$ 建模多路复用网络的层之间的不对称影响。
  现在，我们将不同中心的比较方法应用到一个经典示例中：佛罗伦萨128-1500年文艺复兴时期家庭的社交网络。该网络的数据集（在[27]中可用）收集有关婚姻和商务联系的信息佛罗伦萨的16个复兴家庭中。可以将此社会系统建模为具有两层的多路复用网络：一层与业务联系（特别是记录的财务联系，例如贷款，信贷和共同合伙关系）相关，另一层则显示了16个家庭的总数据集中的婚姻关系（参见[28，29]）。这两个层在图1中表示。
  图2中显示了文艺复兴时期佛罗伦萨家庭的社会多元化网络的不同集中度度量之间的比较。更准确地说，我们表示依赖q的Spearman（红色）和Kendall（在在此特定示例中，投影图的特征向量中心性，均匀中心性，局部异构中心性和全局异构中心性之间的相关系数。


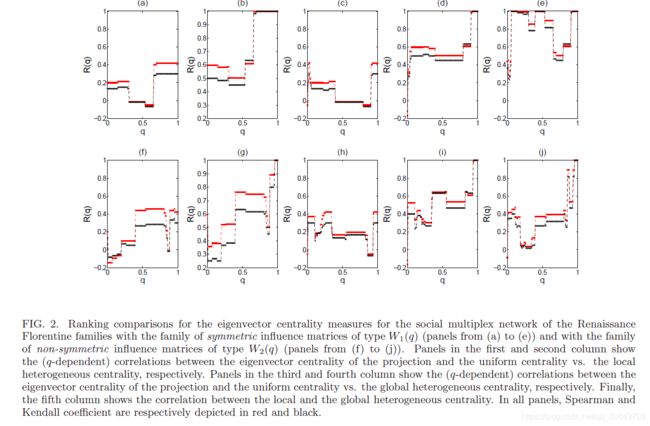
  文艺复兴时期佛罗伦萨家庭与 $W_1(q)$ 型对称影响矩阵族（从 $(a)$ 到$(e)$ ）和非对称影响族裔的社会多重网络的本征中心性度量的等级比较 $W_2(q)$ 类型的矩阵（从$(f)$ 到 $(j)$ 的面板）。 第一列和第二列中的面板分别显示了投影的特征向量中心点与均匀中心点与局部异质中心点之间的（q相关）相关性。 第三列和第四列中的面板分别显示了投影的特征向量中心和均匀中心与全局异构中心之间的（q相关）相关性。 最后，第五列显示了局部和全局异构中心性之间的相关性。 在所有面板中，Spearman和Kendall系数分别用红色和黑色表示。