第十届蓝桥杯大赛软件类省赛C++研究生组
这比赛题目
- A 立方和(5,√)
- B 字串数字(5, √)
- C 质数(10, √)
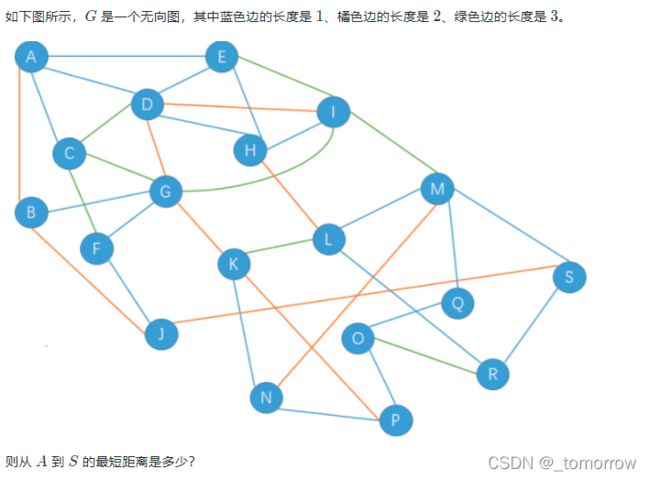
- D 最短路(10, √)
- E RSA解密(15)
- F Fibonacci数列与黄金分割(15, √)
- G 扫地机器人(20,√)
- H 修改数组(20,√)
- I 灵能传输(25)
- J 空间跳跃
写在前面:题目是全的,但是由于能力有限,有些题没有完成,每道题的分值及完成情况已在题目后面注明
A 立方和(5,√)
题目描述
小明对数位中含有2、0、1、9的数字很感兴趣,在1到40中这样的数包括1、2、9、10至32、39和40,共28个,他们的和是574,平方和是14362,立方和是400816。
请问,在1到2019中,所有这样的数的立方和是多少?
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
暴力求解,注意立方和的范围,用long long 表示
#define _CRT_SECURE_NO_WARNINGS
#include B 字串数字(5, √)
结合字母的位置进行计算
AA = 261 * 1 + 1
AB = 261 * 1 + 2
AZ = 261 * 1 + 26
LQ = 261 * 1 + 17
第i位的数字需要26i-1 乘该字母对应的数字,最后求和
#define _CRT_SECURE_NO_WARNINGS
#include C 质数(10, √)
题目描述
我们知道第一个质数是 2、第二个质数是 3、第三个质数是 5……
请你计算第 2019 个质数是多少?
暴力求解。注意循环的时候条件num是小于2019,最终求得的结果i需要减一个数
#define _CRT_SECURE_NO_WARNINGS
#include D 最短路(10, √)
搜索与回溯,直接用dfs求解
#include E RSA解密(15)
RSA 是一种经典的加密算法。它的基本加密过程如下。
首先生成两个质数 p, q,令 n = p · q,设 d与 (p − 1) · (q − 1)互质,则可找到 e 使得 d · e 除 (p − 1) · (q − 1)的余数为 1。
n,d,e 组成了私钥,n, d 组成了公钥。
当使用公钥加密一个整数 X 时(小于 n),计算 C = Xd mod n,则 C 是加密后的密文。
当收到密文 C 时,可使用私钥解开,计算公式为 X = Cemod n。
例如,当 p = 5, q = 11, d = 3 时,n = 55, e = 27。
若加密数字 24,得 243 mod 55 = 19。 解密数字 19,得 1927 mod 55 = 24。
现在你知道公钥中 n = 1001733993063167141, d = 212353,同时你截获了别人发送的密文 C = 20190324,请问,原文是多少?
看网上的解析需要了解别的函数,有些麻烦
F Fibonacci数列与黄金分割(15, √)
题目描述
Fibonacci 数列是非常著名的数列:
F[1] = 1,
F[2] = 1,
对于 i > 3,F[i] = F[i−1] + F[i−2]。
Fibonacci 数列有一个特殊的性质,前一项与后一项的比值,F[N]/F[N + 1], 会趋近于黄金分割。
为了验证这一性质,给定正整数 N,请你计算 F[N]/F[N + 1],并保留 8 位小数。
输入描述
输入一个正整数 N\ (1 <= N ≤2×10 9)。
输出描述
输出 F[N]/F[N + 1]。答案保留 8 位小数。
输入输出样例
输入
2
输出
0.50000000
直接暴力,但是需要注意一点,当n大于20时,得到的结果都是一样的,所以,对于大于n的值,直接使n等于20即可
#define _CRT_SECURE_NO_WARNINGS
#include G 扫地机器人(20,√)
题目描述
小明公司的办公区有一条长长的走廊,由 NN 个方格区域组成,如下图所示。

走廊内部署了 K 台扫地机器人,其中第 i 台在第 Ai个方格区域中。已知扫地机器人每分钟可以移动到左右相邻的方格中,并将该区域清扫干净。
请你编写一个程序,计算每台机器人的清扫路线,使得
- 它们最终都返回出发方格,
- 每个方格区域都至少被清扫一遍,
- 从机器人开始行动到最后一台机器人归位花费的时间最少。
注意多台机器人可以同时清扫同一方块区域,它们不会互相影响。
输出最少花费的时间。 在上图所示的例子中,最少花费时间是 6。第一台路线:2-1-2-3-4-3-2,清 扫了 1、2、3、4 号区域。第二台路线 5-6-7-6-5,清扫了 5、6、7。第三台路线 10-9-8-9-10,清扫了 8、9 和 10。
输入描述
第一行包含两个整数 N,K。
接下来 KK 行,每行一个整数 Ai 。
其中,1≤K
输出描述
输出一个整数表示答案。
输入输出样例
输入
10 3
5
2
10
输出
6
首先确定一点,设某个机器人的清扫区域长度为s,则需要的时间为2*(s-1)。
分两步讨论,首先随机找到机器人清扫的区域长度x,然后需要判断x能否清理完所有区域。 (1)清扫区域的长度范围为[1,n],求机器人最短的路径长度,用二分会比从1到n遍历快一些。
(2)判断对于每个区域长度。当Ai机器人开始清扫时,需要针对当前已清扫的区域total确定Ai的清扫范围。分两种情况:
2.1 total < arr[i] - x,即使Ai往左扫x个区域,都和前面已清扫的区域连接不上,直接返回false
2.2 total >= arr[i] - x,Ai往左清扫可以与以清扫区域连接上,又分两种情况:
2.2.1 total < arr[i],Ai在已清扫区域右边,即上一个机器人到不了Ai,直接从当前位置找到清扫的最远范围,total+= x
2.2.2 total >= arr[i],上一个机器人可以扫过Ai,则total需要从Ai位置开始算,total=arr[i]+x-1
#define _CRT_SECURE_NO_WARNINGS
#include H 修改数组(20,√)
5
2 1 1 3 4
输出
2 1 3 4 5
思路:并查集,直接使用一个数组来表示某个数是否被占用,不实际,数有可能会非常大。
用数组a表示每个节点的父节点,findf(x)为找到x节点的父节点。题目要求若有相同的数则需要不断+1至某数未出现过,因此每次更新父节点时,就需要在该节点当前的父节点基础上+1。
#define _CRT_SECURE_NO_WARNINGS
#include I 灵能传输(25)
3
3
5 -2 3
4
0 0 0 0
3
1 2 3
输出2
3
0
3
/**
样例说明:
对于第一组询问:
对2号高阶圣堂武士进行传输操作后,a1=3,a2=2, a3=1.答案为3.
对于第二组询问:
这一组高阶圣堂武士拥有的灵能都正好可以让他们大都最佳战斗状态。
*/
输入2:
3
4
-1 -2 -3 7
4
2 3 4 -8
5
-1 -1 6 -1 -1
输出2
5
7
4
J 空间跳跃
3 2 3
1 2 2 1
1 2 4 1
输出1
6
4 4 7
1 2 2 7
1 3 4 6
2 4 6 3
3 4 3 2
输出2
9.3333333333
输入3:
5 7 12
1 3 5 5
4 5 7 9
2 5 8 1
3 5 4 4
1 2 3 3
3 4 3 1
2 4 2 5
输出3
11.3571428571