机器人图规划算法研究现状简述

‍

[文末提供原文PDF免费下载(期刊论文版式)]‍‍

摘要：运动规划是移动机器人自主导航系统中的重要模块之一，相关算法研究成果层出不穷，本文将图规划算法拆解为三个子类算法：图搜索算法、BUG类算法和势场力类算法，并沿时间顺序概述相关算法的发展历程，最后从模型复杂度、实时性、环境适应能力及路径曲线质量等方面分析了上述三类算法的优缺点。

01 引言

我们从两个问题切入正题：运动规划是什么？要解决什么问题？

如图 1.1所示，对机器人而言，所谓运动规划，就是在一张地图上生成从起始点到目标点的轨迹（轨迹曲线=路径曲线+速度曲线），并控制机器人沿着这条轨迹运动，直至目标。所以，我们可以看到运动规划就是要解决机器人从A点如何顺利到B点的问题，顺利这个词翻译成优化目标，可以是最短时间，也可以是最短路径等。

图 1.1 运动规划示意图（图片来源：http://wiki.ros.org/navigation）

从上述可知，要进行运动规划，需要有两个前提条件：地图和定位。机器人需要先利用传感器获取环境信息，构建环境地图并计算自身在环境地图中的位姿（见《机器人环境感知研究现状简述》），接着根据自身在地图中的位置，明确起始点和终点后，才可以进入到运动规划阶段，最后将生成的轨迹转化为运动控制命令发送给运动控制模型（见《常见移动机器人运动学模型总结》），驱动机器人运动。

如图 1.2所示，运动规划的研究主要是对多目标多变量多约束耦合的规划模型优化求解。对于具有非完整约束的移动机器人而言（见《两轮差速驱动机器人运动模型及应用分析》），在分布有障碍物的环境中求解最优路径是NP-hard问题，即对于任意场景无法保证在多项式时间内求得最优解，因此大部分规划算法追求次优解或局部最优[1]。

诸多学者针对不同应用场景和需求，设计、改进了非常多的运动规划算法，其中常见的运动规划算法主要包括四类：图规划算法、空间采样算法、曲线插值拟合算法和仿生智能算法，通过规划模型求解得到最佳轨迹曲线，包含无碰撞顺滑的路径曲线和平滑的速度曲线，并输入到控制器驱动机器人运动。

本文将对图规划算法领域的研究进展及成果进行分类阐述，主要概述同族算法的发展过程，不对具体算法展开分析，在后续系列文章会挑选部分经典常用算法深入剖析。

图 1.2 运动规划通用模型

02 图规划算法研究分析

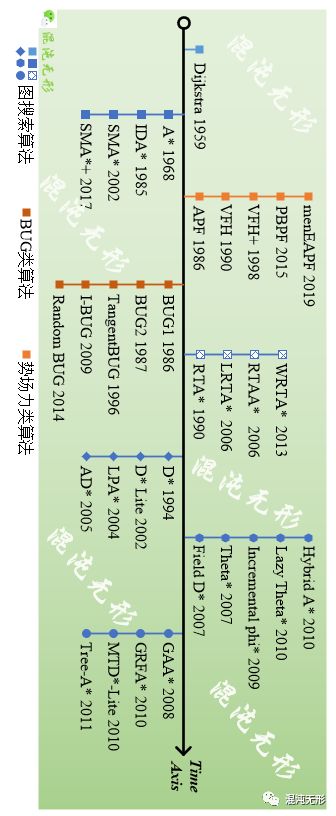
图规划算法多数将环境模型离散化表达，如栅格图等，其离散节点描述相应状态，建立节点间联系，并求解最优路径。如图 2.1所示，图规划算法根据路径生成方式的不同分为三类，其中以图搜索算法为主，以及BUG算法和势场力算法，具体如下：

（请横屏看图）

图 2.1 图规划算法发展路线概况

2.1图搜索算法

第一类是图搜索算法，此类算法的主要特征是将地图栅格化后进行路径搜索，并致力于达到路径最短、效率最优等目标。

如图 2.2所示，Dijkstra算法是最经典的图搜索算法之一，属于广度优先算法，采用遍历的方式，计算起点到终点的所有路径，并选择成本最低的路径，因此可搜索最短路径（网上有大量资料，故不赘述）。

图 2.2 Dijkstra算法（图片来源：https://github.com/AtsushiSakai/PythonRobotics）

A*算法在Dijkstra算法基础之上，根据起始点和终止点的先验信息设计巧妙的启发式函数，减少搜索扩展的节点数，提高了路径搜索效率。（补充：后续算法名中带有*的算法，基本上暗含该算法采用了启发式函数）

图 2.3 A*算法（图片来源：https://github.com/AtsushiSakai/PythonRobotics）

针对A*算法在实际应用中的不足之处，后续研究者从内存消耗、实时性、动态环境适应性、移动目标追踪、路径质量等角度进行了深入研究和改进，具体如下：

• 内存消耗改进

  Korf、Chakrabarti、Zhou及Lovinger等人对此改进了A*算法，如IDA*[2]采用有限度的迭代加深（深度优先）算法，通过评价函数剪枝优化，降低了搜索内存消耗。SMA*[3]仅在超过设定内存空间时，才开始剪枝，并从open list储存数据结构、f-cost需求数量及节点备份与删除等方面简化改进。与SMA*不同，SMA*+[4]设计节点剔除启发式函数，在有限内存空间限制下，通过搜索空间的先验知识进一步提高了搜索性能。

• 实时性改进

  实时性一直是算法评估的重要指标之一，在有限时间内搜索一条可行路径更具实用意义。Korf、Bulitko、Koenig及Rivera等人对此改进A算法，RTA*[5]与LRTA*[6]在迁移到下一节点之前会更新启发值h，RTA*[5]选择第二小的成本更新节点h，LRTA*则选择最小值，相应的，RTA*在单次试验中的学习率更高，在相同的目标状态但不同的初始状态的情况下重复求解，LRTA*将随着时间的推移而提高效率，并最终收敛于最优解。RTAA*[7]则使用open list中的最佳节点的g值更新h值，以朝向A*规划方向搜索。虽然提高实时性，但却不能保证为最优路径。WRTA*[8]采用加权更新的方式，通过使用不同的学习规则将权重值w合并到h中，在计算成本和总搜索时间方面有极大改进。

• 动态环境适应性改进

  机器人运动场景多是动态、连续变化的，因此在动态环境中的相邻两次搜索得到的路径相似度较高，即路径局部一致性。Stentz、Koenig、Koenig和Likhachev等人基于重用已搜索节点信息的效率高于完全重新计算效率的基本思路改进A*算法，如D*[9]算法采用贪心算法从目标点反向搜索到机器人当前位置，并根据动态障碍物信息调整路径，并被应用于HMMWVs和Mars Rover机器人。不同于D*，LPA*[10]总能找到从初始固定起点到初始固定终点的最优路径，但不适用于机器人运动场景，D* Lite[11]改进LPA*，其节点的启发函数值随着起点的变化而变化，相较于D*，搜索效率得到提升，且实现过程得到简化。AD*[12]在此基础上考虑时间约束，能够在有限时间内重规划次优路径，极大提升机器人在动态环境中的实用性。

• 移动目标追踪改进

  当目标点动态变化时，上述适应动态环境算法的搜索效率将会降低，Sun、Hernández等人对此研究改进。GGA*[13]将三个状态点（当前点、下一点、目标点）纳入三角不等式以更新启发值，GFRA*[14]高效地将上移搜索树转化到当前搜索树，极大提高移动目标的效率，但无法适用于动态环境，而MTD*-Lite[15]在D*-Lite算法基础上借鉴GFRA*重用上一次搜索结果的思想，搜索效率提高到了GGA*的3-7倍。Tree-AA*[16]可重用当前及以前所有的A*搜索结果（可重用树），实现最优增量启发式路径搜索。

• 路径质量改进

  普通栅格地图搜索算法，其节点移动方向仅能为π/4的整数倍，因此Ferguson、Nash和Dolgov等人针对路径存在大量“细碎”折线段的问题提出了改进方法，如Field D*[17]是D* Lite的变种，节点能够沿任何方向扩展，而Theta*[18]是A*的变种，能够得到比Field D*更短的路径，但重规划不如Field D*，Incremental Phi*[19]结合了Theta*和D* Lite的优势，能够快速规划最优路径，Lazy Theta*[20]是Theta*的变种，降低了line-of-sight check次数，在不增加路径长度的同时，显著提升搜索效率。如图 2.4所示，Hybrid A*[21]在A中融入RS曲线约束，满足最小转弯半径约束，进一步提高路径连续性，并成功应用于无人车Junior。

图 2.4 Hybrid A*[21]

2.2BUG类算法

第二类算法为BUG算法，是基于几何地图规划的算法，如图 2.5所示，其核心思路是当机器人遇到障碍物时，就沿着障碍物边界运动，没有遇到障碍物时候，就沿着起点到终点的连线方向上运动。

图 2.5 BUG算法（图片来源：https://www.researchgate.net/figure/Trajectory-of-dist-bug-algorithm_fig1_324562768）

基于上述思路，诸多学者进行了研究升级。Lumelsky、Kamon、Taylor和Xu等人提出的BUG类型算法在特征地图中能够（近似）沿障碍物轮廓运动到目标点。BUG2[22]相较于BUG1[23]缩短路径长度，而Tangent BUG[24]通过传感器提前避障，使路径更平滑。I-BUG结合信标信号的强弱，降低里程累积误差，如图 2.6所示，Random BUG[25]中应用了随机树，可选择最佳局部目标点以优化路径。BUG类算法极依赖于全局定位，但其简单高效等特点可被应用于微型机器人自主导航。

图 2.6 Random BUG[25]

2.3势场力类算法

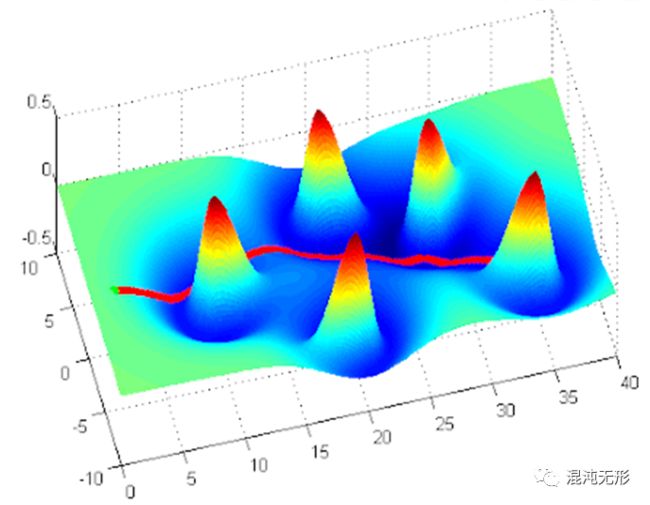
第三类算法是人工势场法，是借鉴了重力势场和电场模型，如设定障碍物对机器人产生排斥力，目标点对机器人产生吸引力，将所有排斥力和吸引力进行矢量合成，其合力方向便是机器人的运动方向，合力大小被转化为机器人运动加速度大小，当机器人运动到目标点时，合力为0，也恰好停止运动。

图 2.7 人工势场法[26]

诸多学者对人工势场法展开研究，并设计出了诸多算法。如图 2.7所示，传统势场法APF[26]基于特征地图构造势场力模型，驱动机器人沿合力最小的方向运动，在存在局部最小值等问题，由此Borenstein、Ulrich和Orozco-Rosas等人进行深入研究，如VFH[27]使用直方图描述环境等距采样信息，并确定机器人运动方向，VFH+[28]基于此的改进包括：阈值滞后、机器人形状及成本函数，提升运动平滑性。与其他算法相结合，如PBPF[29]基于细菌势场法改进变异规则，其并行运算方式可快速生成最优路径。menEAPF[30]将膜计算与遗传算法结合，融入势场模型，以加快遗传算法收敛速度。势场力算法具有模型简洁、计算高效，且避障效果好等优点，但多数势场法未考虑机器人模型硬约束。

03 图规划算法分析

上述三类图规划算法各有各的特点。

图搜索算法的基本原理就是计算所有途径节点的路径的成本值，并选择成本值最低的一条作为结果。

• 主要优点：实时性较好，能够快速全局最优（次优）路径，能适应低维空间的动静态环境，分辨率完备（相较于基于采样的算法，图搜索算法接近于遍历算法）。

• 主要缺点：生成的路径连续性较差，并不适合直接应用于机器人运动，但图搜索算法在高维空间搜索性能不可靠，原因在于在二维空间中，图搜索算法是基于当前点向四周扩展，需要遍历计算四周扩展节点的累加成本，而在三维或更高维空间中，其四周扩展节点数量将迅速增加，这会增加每一次节点扩展时的计算成本，因此在高维空间的搜索性能会严重下降。

BUG类算法的基本原理就是遇到障碍物就沿着障碍物边缘运动，所以实际生成的路径曲线与障碍物边缘曲线形态有着密切关系，可以近似认为是障碍物边界向外缩放后的曲线。

• 主要优点：模型简洁，实时性好，由于主要策略是沿着障碍物边缘运动，所以有着较高的计算效率。

• 主要缺点：依赖于全局定位，抗干扰能力较弱，尤其是在复杂迷宫场景下，BUG算法要找出一条效率高的路径是非常有挑战的。

势场力类算法的基本原理就是构造合适的势场，通过合力驱动机器人运动，当场景中存在较多动态障碍物时，机器人的运动行为也将受到较大的影响。

• 主要优点：模型简洁，安全性极佳，实时性好，路径较平滑。由于计算模型较为简单，因此计算效率较高，能够保证实时性，同时机器人距离障碍物越近，则受到的排斥力越大，保证了安全性。

• 主要缺点：易受到障碍物冲击，存在振荡，当存在多个动态障碍物时，可能会迫使机器人朝着目标反方向运动，而在经过某些特殊场景时，机器人运动轨迹可能会产生震荡，并陷入局部最小值而停止运动。

总体而言，图规划算法已经能够在诸多场景下的规划生成一条无碰撞路径，比如A*算法就被作为ROS navigation stack中global planner的默认算法，随着诸多学者的改进升级，图规划算法的实时性和动态适应性逐渐提升，但多数算法仍存在路径质量差、未考虑动力学约束等问题，这些问题也导致相关算法不能直接应用于实际机器人运动场景。

04 结论与展望

本文将图规划算法拆解为三个子类算法：图搜索算法、BUG类算法和势场力类算法，并沿时间先后顺序概述了相关类型算法的发展改进历程，接着从模型复杂度、计算实时性、动态环境适应能力及路径曲线质量等方面分析了上述三类算法的优缺点，并指出存在的相关问题。

运动规划算法种类繁多，应用场景各不相同，而本文仅概述分析了四类运动规划算法之一的图规划算法，后续会分析其他三类。

（文章仅笔者个人分析，有误请指正，谢谢！）

参考资料

[1] CADENA C, CARLONE L, CARRILLO H, et al. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age [J]. IEEE Transactions on robotics, 2016, 32(6): 1309-32.

[1] REIF J, WANG H. The complexity of the two dimensional curvature-constrained shortest-path problem; proceedings of the Third International Workshop on Algorithmic Foundations of Robotics, F, 1998 [C].

[2] KORF R E. Depth-first iterative-deepening: An optimal admissible tree search [J]. Artificial intelligence, 1985, 27(1): 97-109.

[3] ZHOU R, HANSEN E A. Memory-Bounded A* Graph Search; proceedings of the FLAIRS conference, F, 2002 [C].

[4] LOVINGER J, ZHANG X. Enhanced Simplified Memory-bounded A Star (SMA*+); proceedings of the GCAI, F, 2017 [C].

[5] KORF R E. Real-time heuristic search [J]. Artificial intelligence, 1990, 42(2-3): 189-211.

[6] BULITKO V, LEE G. Learning in real-time search: A unifying framework [J]. Journal of Artificial Intelligence Research, 2006, 25(119-57.

[7] KOENIG S, LIKHACHEV M. Real-time adaptive A; proceedings of the Proceedings of the fifth international joint conference on Autonomous agents and multiagent systems, F, 2006 [C]. ACM.

[8] RIVERA N, BAIER J A, HERNáNDEZ C. Weighted real-time heuristic search; proceedings of the Proceedings of the 2013 international conference on Autonomous agents and multi-agent systems, F, 2013 [C]. International Foundation for Autonomous Agents and Multiagent Systems.

[9] STENTZ A. Optimal and efficient path planning for partially known environments [M]. Intelligent Unmanned Ground Vehicles. Springer. 1997: 203-20.

[10] KOENIG S, LIKHACHEV M, FURCY D. Lifelong planning A∗ [J]. Artificial Intelligence, 2004, 155(1-2): 93-146.

[11] KOENIG S, LIKHACHEV M. D^* lite [J]. Aaai/iaai, 2002, 15

[12] LIKHACHEV M, FERGUSON D I, GORDON G J, et al. Anytime Dynamic A*: An Anytime, Replanning Algorithm; proceedings of the ICAPS, F, 2005 [C].

[13] SUN X, KOENIG S, YEOH W. Generalized adaptive A; proceedings of the Proceedings of the 7th international joint conference on Autonomous agents and multiagent systems-Volume 1, F, 2008 [C]. International Foundation for Autonomous Agents and Multiagent Systems.

[14] SUN X, YEOH W, KOENIG S. Generalized Fringe-Retrieving A* faster moving target search on state lattices; proceedings of the Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems: volume 1-Volume 1, F, 2010 [C].

[15] SUN X, YEOH W, KOENIG S. Moving target D* lite; proceedings of the Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems: volume 1-Volume 1, F, 2010 [C].

[16] HERNáNDEZ C, SUN X, KOENIG S, et al. Tree adaptive a; proceedings of the The 10th International Conference on Autonomous Agents and Multiagent Systems-Volume 1, F, 2011 [C].

[17] FERGUSON D, STENTZ A. Field D*: An interpolation-based path planner and replanner [M]. Robotics research. Springer. 2007: 239-53.

[18] NASH A, DANIEL K, KOENIG S, et al. Theta^: Any-angle path planning on grids; proceedings of the AAAI, F, 2007 [C].

[19] NASH A, KOENIG S, LIKHACHEV M. Incremental Phi: Incremental any-angle path planning on grids; proceedings of the Twenty-First International Joint Conference on Artificial Intelligence, F, 2009 [C].

[20] NASH A, KOENIG S, TOVEY C. Lazy Theta*: Any-angle path planning and path length analysis in 3D; proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, F, 2010 [C].

[21] DOLGOV D, THRUN S, MONTEMERLO M, et al. Path planning for autonomous vehicles in unknown semi-structured environments [J]. The International Journal of Robotics Research, 2010, 29(5): 485-501.

[22] LUMELSKY V J, STEPANOV A A. Path-planning strategies for a point mobile automaton moving amidst unknown obstacles of arbitrary shape [J]. Algorithmica, 1987, 2(1-4): 403-30.

[23] LUMELSKY V, STEPANOV A. Dynamic path planning for a mobile automaton with limited information on the environment [J]. IEEE transactions on Automatic control, 1986, 31(11): 1058-63. [24] KAMON I, RIVLIN E, RIMON E. A new range-sensor based globally convergent navigation algorithm for mobile robots; proceedings of the Proceedings of IEEE International Conference on Robotics and Automation, F, 1996 [C]. IEEE.

[25] TAYLOR K, LAVALLE S M. I-Bug: An intensity-based bug algorithm; proceedings of the 2009 IEEE International Conference on Robotics and Automation, F, 2009 [C]. IEEE.

[26] KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots [M]. Autonomous robot vehicles. Springer. 1986: 396-404.

[27] BORENSTEIN J, KOREN Y. Real-time obstacle avoidance for fast mobile robots in cluttered environments; proceedings of the Proceedings, IEEE International Conference on Robotics and Automation, F, 1990 [C]. IEEE.

[28] ULRICH I, BORENSTEIN J. VFH+: Reliable obstacle avoidance for fast mobile robots; proceedings of the Proceedings 1998 IEEE international conference on robotics and automation (Cat No 98CH36146), F, 1998 [C]. IEEE.

[29] OROZCO-ROSAS U, MONTIEL O, SEPúLVEDA R. Pseudo-bacterial potential field based path planner for autonomous mobile robot navigation [J]. International Journal of Advanced Robotic Systems, 2015, 12(7): 81.

[30] OROZCO-ROSAS U, MONTIEL O, SEPúLVEDA R. Mobile robot path planning using membrane evolutionary artificial potential field [J]. Applied Soft Computing, 2019, 77(236-51.

福利放送

笔者为小伙伴们整理了期刊论文版式原文PDF，方便收藏和回味

链接：https://pan.baidu.com/s/1wCb0uf8-zHttmzMWkW8EgQ

提取码：z5eb

若链接失效，可在后台回复本文标题或发送邮件：[email protected]

延伸阅读

机器人环境感知研究现状简述

常见移动机器人运动学模型总结

常见移动机器人多角度对比分析

Car-like robot运动参数校准

差速驱动机器人轮间距校准

常见移动机器人轮直径校准

全向移动机器人运动参数校准

-----------------------------------------------------------------------------

相关声明

1.如果转载本文，文末务必注明：“转自微信公众号：混沌无形”

2.若有侵权，请联系作者

全文完，感谢阅读！！如果觉得写的不错，那就点个赞或者“在看”吧。

混沌无形

混沌系统是世界本质，无形之中存在规律。机器人智能化发展从线性过渡到混沌，本号将分享机器人全栈技术（感知、规划、控制；软件、机械、硬件等）。

41篇原创内容

公众号