机器学习-卷积神经网络CNN中的单通道和多通道图片差异

背景

最近在使用CNN的场景中，既有单通道的图片输入需求，也有多通道的图片输入需求，因此又整理回顾了一下单通道或者多通道卷积的差别，这里记录一下探索过程。

结论

直接给出结论，单通道图片和多通道图片在经历了第一个卷积层以后，就没有单通道或者多通道的区别了，剩下的网络可以采取完全一样的结构。这也为我们使用各种各样的网络架构，resnet，Alexnet，vgg提供了方便，因为他们都是为了跑ImageNet而设计的特定输入。

图解

1.成员介绍

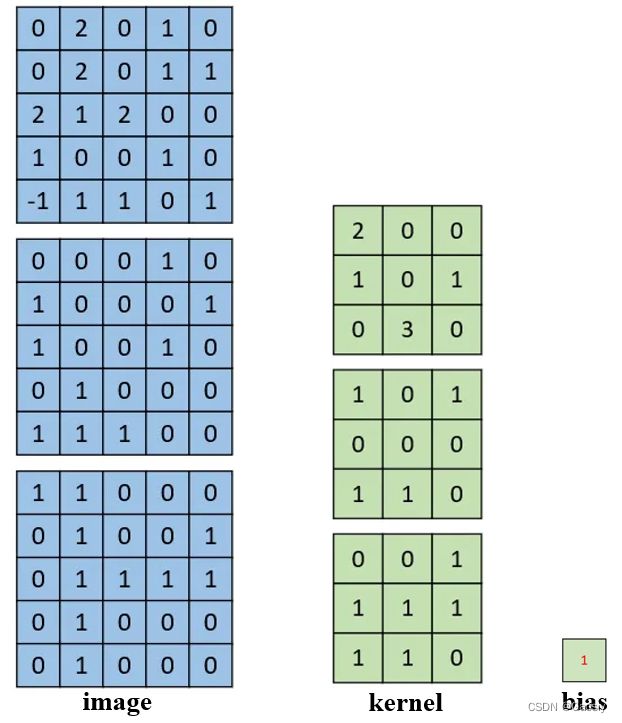
在CNN中涉及到的主要就是image kernel bias这三个元素。这里image表示是首层的输入，后边卷积层的impute都是前边的output，与首层操作类似，不再多说。

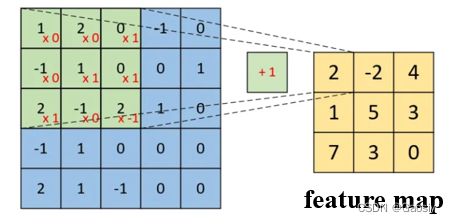
2.单通道图片卷积过程

可以看到，通过对应位置相乘再相加，结合bias，最终得到feature map中的一个元素，所以卷积核的一次计算只得到一个数。当卷积核刷遍整张图片以后，得到了一个完整的feature map。这个东西将作为下一层的输入，传递下去。

通常来说，我们的卷积层不会只有一个kernel，因为一个kernel只能提取图片的一类特征，我们使用CNN的目的就在于应用多个kernel学习到多个特征，下面给出使用两个kernel的例子。

每一个kernel都会来一遍上图中获得feature map的过程。最终我们会得到2个feature map，与卷积核的数量一致。

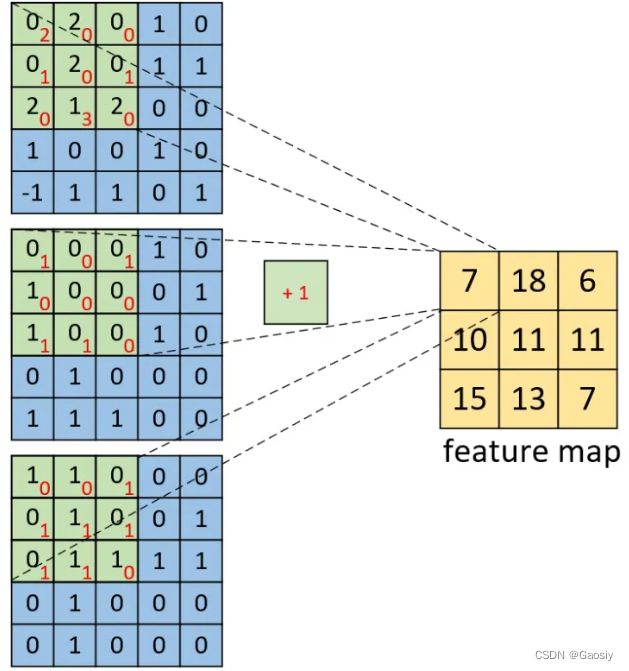
2.RGB三通道图片卷积过程

 

这里可以看到，图片从一个矩阵变为了3个，这时候kernel也变成了3个矩阵，请注意 ，这三个叫做一个kernel，但是这三个kernel共享一个bias。在卷积运算的时候，这个kernel的三个通道分别与对应的图片通道做卷积，过程与单通道处理是一样的，但是这里由于有三个通道，所以会得到3个数字，而不是之前的一个数字，但是这里的三个数字会直接相加，最终还是一个数字，所以这里就是3通道卷积的trick所在，这里是容易疑惑的一个点，搞明白就好。

多个kernel可以类比之前的单通道，总之，结论就是，不管是单通道还是三通道的首个卷积层，都会输出与kernel数量相等的feature map。且不管是不是单通道，只要图片宽高是一样的，单通道和多通道的首个卷积层过后，得到的feature map在维度上是一致的。

 

代码验证

选择了pytorch中的torch.nn.Conv2d来做验证。

1.简单介绍网络的输入参数含义

import torch.nn as nn

# 定义一个二维卷积层
conv_layer = nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3, stride=1, padding=1)

# 假设有一个4维的输入张量 x，形状为 (batch_size, in_channels, height, width)
x = torch.randn(1, 3, 32, 32)

# 在输入张量上应用卷积层
output = conv_layer(x)

# 输出张量的形状为 (batch_size, out_channels, output_height, output_width)

其中，in_channels表示输入张量的通道数，out_channels表示输出张量的通道数（即卷积核的数量），kernel_size表示卷积核的大小，stride表示卷积的步长，padding表示边缘填充的大小。在输入张量上应用卷积层后，输出张量的形状为 (batch_size, out_channels, output_height, output_width)。 

2.为单通道图片设计第一个卷积层，并查看该层的输出

# 设计一个单通道的卷积网络结构
import torch
from torch.autograd import Variable
# 单通道图片模拟输入
input=torch.ones(1,1,64,64)
input=Variable(input)
x=torch.nn.Conv2d(in_channels=1,out_channels=5,kernel_size=3,groups=1)
out=x(input)
print(out.shape)
print(list(x.parameters()))

打印结果

torch.Size([1, 5, 62, 62])
[Parameter containing:
tensor([[[[-0.1166,  0.2381, -0.0446],
          [ 0.0855,  0.1347, -0.2986],
          [-0.3251,  0.2721,  0.2473]]],


        [[[-0.1630,  0.2612,  0.1867],
          [-0.1606, -0.2781, -0.1183],
          [ 0.2221, -0.1114, -0.2046]]],


        [[[-0.2414, -0.2379,  0.0680],
          [ 0.1928, -0.0585,  0.1804],
          [ 0.1891, -0.1915,  0.0281]]],


        [[[-0.3227,  0.0911, -0.0136],
          [-0.2742, -0.2246, -0.1227],
          [ 0.1420,  0.3284, -0.0288]]],


        [[[ 0.2173, -0.1299, -0.2056],
          [-0.2324,  0.2499, -0.1909],
          [ 0.2416, -0.1457, -0.1176]]]], requires_grad=True), 
Parameter containing:
tensor([-0.0273,  0.2994,  0.3226, -0.2969,  0.2965], requires_grad=True)]

这里我们可以看到，第一层的输出结果是有5个feature maps，也就是卷积核的数量。随后我们打印出了第一层的卷积参数，可以看到就是5个卷积核的参数，以及对应的五个bias参数。

3.为RGB三通道图片设计第一个卷积层，并给出参数

# 设计一个3通道的卷积网络结构
import torch
from torch.autograd import Variable
# 模拟RGB三通道图片输入
input=torch.ones(1,3,64,64)
input=Variable(input)
x=torch.nn.Conv2d(in_channels=3,out_channels=5,kernel_size=3,groups=1)
out=x(input)
print(out.shape)
print(list(x.parameters()))

打印输出

torch.Size([1, 5, 62, 62])
[Parameter containing:
tensor([[[[-0.0902, -0.0764,  0.1497],
          [-0.0632, -0.1014, -0.0682],
          [ 0.1309,  0.1173,  0.0268]],

         [[-0.0410, -0.1763,  0.0867],
          [ 0.0771, -0.0969,  0.0700],
          [ 0.1446, -0.0159, -0.1869]],

         [[-0.1278,  0.0244,  0.1861],
          [-0.0180,  0.0529, -0.1475],
          [-0.0562, -0.0487,  0.0659]]],


        [[[ 0.0649, -0.1758, -0.0420],
          [ 0.1287,  0.1500,  0.1027],
          [ 0.0033,  0.1565,  0.1461]],

         [[ 0.0645,  0.0515, -0.0729],
          [ 0.0900,  0.0941,  0.1813],
          [ 0.1846, -0.1075,  0.1861]],

         [[ 0.1489,  0.0536,  0.1510],
          [-0.1070,  0.0748,  0.1619],
          [ 0.1812, -0.0722,  0.1492]]],


        [[[-0.0450, -0.0846,  0.0761],
          [ 0.1049,  0.0492,  0.1556],
          [ 0.1301,  0.0494,  0.0136]],

         [[-0.1303, -0.0979, -0.0331],
          [ 0.0435, -0.0201, -0.1207],
          [ 0.1275, -0.0049, -0.0092]],

         [[ 0.1782,  0.1347,  0.0707],
          [-0.0850,  0.0585,  0.1361],
          [ 0.0917, -0.0156,  0.0407]]],


        [[[ 0.0491,  0.0752,  0.0096],
          [ 0.1599, -0.1281, -0.0937],
          [ 0.1029, -0.1467,  0.1238]],

         [[-0.0651, -0.1169,  0.1772],
          [ 0.0180,  0.1491,  0.0145],
          [ 0.0586,  0.1246,  0.1060]],

         [[-0.1220,  0.0525,  0.1046],
          [ 0.0069,  0.0356,  0.0152],
          [-0.0822, -0.1157, -0.0420]]],


        [[[-0.0679,  0.1752,  0.1020],
          [ 0.0018,  0.0721,  0.1708],
          [-0.0201,  0.1753,  0.0620]],

         [[-0.0023, -0.1203, -0.1113],
          [ 0.1765, -0.1914,  0.0836],
          [-0.0526, -0.1803, -0.0656]],

         [[-0.1735,  0.0795, -0.1867],
          [ 0.1757, -0.0261,  0.0198],
          [-0.1756, -0.0549, -0.0018]]]], requires_grad=True), 
Parameter containing:
tensor([-0.1727,  0.1823,  0.1416, -0.0721, -0.1219], requires_grad=True)]

可以看到，对三通道的图片处理后，输出的也是一样的形状，但是具体再看卷积核，会发现，每个卷积核都有3个通道，而且每个通道的参数是不一样的，但是他们共享一个bias。