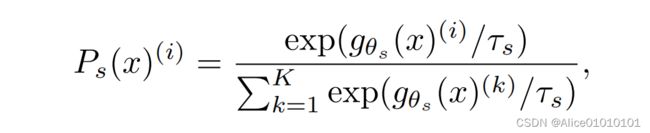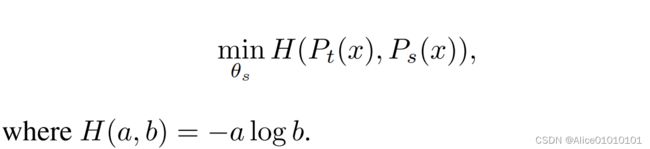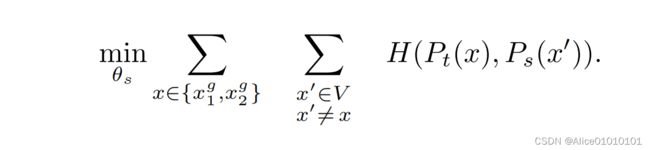- 【分类】【损失函数】处理类别不平衡:CEFL 和 CEFL2 损失函数的实现与应用
丶2136
AI分类人工智能损失函数
引言在深度学习中的分类问题中,类别不平衡问题是常见的挑战之一。尤其在面部表情分类任务中,不同表情类别的样本数量可能差异较大,比如“开心”表情的样本远远多于“生气”表情。面对这种情况,普通的交叉熵损失函数容易导致模型过拟合到大类样本,忽略少数类样本。为了有效解决类别不平衡问题,Class-balancedExponentialFocalLoss(CEFL)和Class-balancedExponen
- 【新人系列】Python 入门(十六):正则表达式
Pandaconda
#Python新人系列python正则表达式开发语言后端笔记面试
✍个人博客:https://blog.csdn.net/Newin2020?type=blog专栏地址:https://blog.csdn.net/newin2020/category_12801353.html专栏定位:为0基础刚入门Python的小伙伴提供详细的讲解,也欢迎大佬们一起交流~专栏简介:在这个专栏,我将带着大家从0开始入门Python的学习。在这个Python的新人系列专栏下,将会
- 【新人系列】Python 入门(十七):类与对象
Pandaconda
#Python新人系列python开发语言后端笔记面试面向对象类
✍个人博客:https://blog.csdn.net/Newin2020?type=blog专栏地址:https://blog.csdn.net/newin2020/category_12801353.html专栏定位:为0基础刚入门Python的小伙伴提供详细的讲解,也欢迎大佬们一起交流~专栏简介:在这个专栏,我将带着大家从0开始入门Python的学习。在这个Python的新人系列专栏下,将会
- 【新人系列】Python 入门(十一):控制结构
Pandaconda
#Python新人系列python开发语言后端笔记面试控制结构经验分享
✍个人博客:https://blog.csdn.net/Newin2020?type=blog专栏地址:https://blog.csdn.net/newin2020/category_12801353.html专栏定位:为0基础刚入门Python的小伙伴提供详细的讲解,也欢迎大佬们一起交流~专栏简介:在这个专栏,我将带着大家从0开始入门Python的学习。在这个Python的新人系列专栏下,将会
- 2024年Python最新Python爬虫入门教程27:爬取某电商平台数据内容并做数据可视化
2401_84584609
程序员python爬虫信息可视化
‘详情页’])csv_writer.writeheader()forpageinrange(1,26):print(f’正在保存第{page}页数据内容===========')url=f’http://bang.dangdang.com/books/bestsellers/01.00.00.00.00.00-year-2017-0-1-{page}’headers={‘User-Agent’:‘
- VSCode 配置python虚拟环境(激活环境细节)_vscode python conda虚拟环境(1)
2401_83817171
程序员vscodepythonconda
AnacondaPrompt常用命令:1.查看存在的环境:condainfo-e2.创建新环境:condacreate-n环境名python=(python的版本号)3.切换到某个环境:condaactivate环境名4.查看环境中已安装的包:condalist5.在环境中安装包:pipinstall包名6.删除包:pipunstall包名7.删除环境:condaenvremove-n环境名下载库
- Python单元测试之道:从入门到精通的全面指南合集
雅雅酱o
log4jpython开发语言编程计算机单元测试
深入探讨Python单元测试的各个方面,包括基本概念、基础知识、实践方法、高级话题,如何在实际项目中进行单元测试,单元测试的最佳实践,以及一些有用的工具和资源。python学习资料、教程分享:一、单元测试重要性测试是软件开发中不可或缺的一部分,它能够帮助我们保证代码的质量,减少bug,提高系统的稳定性。在各种测试方法中,单元测试由于其快速、有效的特性,特别受到开发者们的喜欢。本文将全面介绍Pyth
- Python酷库之旅-第三方库Pandas(181)
神奇夜光杯
pythonpandas开发语言人工智能标准库及第三方库excel学习与成长
目录一、用法精讲836、pandas.api.types.is_file_like函数836-1、语法836-2、参数836-3、功能836-4、返回值836-5、说明836-6、用法836-6-1、数据准备836-6-2、代码示例836-6-3、结果输出837、pandas.api.types.is_list_like函数837-1、语法837-2、参数837-3、功能837-4、返回值837-
- 【Python】serial库的介绍及用法
"啦啦啦"
pythonpython网络linux
目录1、应用场景2、serial-三方库1、应用场景serial库,也被称为pySerial,主要用于串行通信,它在以下几个场景中被广泛应用:嵌入式系统通信:许多嵌入式系统(如Arduino、RaspberryPi等)都使用串行通信进行数据传输。pySerial可以帮助Python程序与这些设备进行通信。硬件设备控制:许多硬件设备(如机器人、传感器、GPS模块等)都使用串行接口进行控制。pySer
- 如何利用 Python抓取网页数据 其他方式抓取网页数据列举
数码小沙
python实例操作pythonphp开发语言
在Python中可以使用多种方法抓取网页数据,以下是一种常见的方法,使用requests和BeautifulSoup库。一、安装所需库在命令提示符或终端中执行以下命令安装requests和BeautifulSoup库:pipinstallrequestspipinstallbeautifulsoup4二、抓取网页数据步骤发送请求使用requests库发送HTTP请求来获取网页内容。例如:impor
- 【新人系列】Python 入门(二十七):Python 库
Pandaconda
#Python新人系列python开发语言后端笔记面试python库库
✍个人博客:https://blog.csdn.net/Newin2020?type=blog专栏地址:https://blog.csdn.net/newin2020/category_12801353.html专栏定位:为0基础刚入门Python的小伙伴提供详细的讲解,也欢迎大佬们一起交流~专栏简介:在这个专栏,我将带着大家从0开始入门Python的学习。在这个Python的新人系列专栏下,将会
- python爬取高德地图道路交通状态数据代码
weixin_17839606517
可视化python开发语言
"""author:17839606517"""importdatetimeimportdatetimeimportosimportcsvfromcodecsimportStreamReaderWriterimportnumpyasnpimportrequestsimportpandasaspdimportjsonimportcodecsimporttimedefaaa():#初始API的URL#
- python雪人_python实现滑雪者小游戏
weixin_39692761
python雪人
引言这是一个用pygame写的滑雪者的游戏。skier从上向下滑,途中会遇到树和旗子,捡起一个旗子得10分,碰到一颗树扣100分,可以用左右箭头控制skier方向。安装pygamepipinstallpygame用pip或设置界面安装,可自行百度以下是主界面代码,每一个类都是一个py文件,需要导包importpygameimportrandomfromsettingsimportSettingsf
- 华为云开天 aPaaS 平台的流使用体验
Python中的class体内定义方法时,如果没有显式地包含self参数,有时候依然可以被调用。这是一个非常有趣的话题,因为它涉及到对Python中类与对象之间关系的更深理解。要理解为什么这种情况下方法依然能够被调用,我们需要逐步拆解Python类的构造方式以及方法绑定的原理。
- 交叉熵损失函数(Cross-Entropy Loss)
我叫罗泽南
深度学习人工智能
原理交叉熵损失函数是深度学习中分类问题常用的损失函数,特别适用于多分类问题。它通过度量预测分布与真实分布之间的差异,来衡量模型输出的准确性。交叉熵的数学公式交叉熵的定义如下:CrossEntroyLoss=−∑i=1Nyi⋅log(y^i)\begin{equation}CrossEntroyLoss=-\sum_{i=1}^{N}y_i\cdotlog(\hat{y}_i)\end{equati
- 什么是多模态机器学习:跨感知融合的智能前沿
非凡暖阳
人工智能神经网络
在人工智能的广阔天地里,多模态机器学习(MultimodalMachineLearning)作为一项前沿技术,正逐步解锁人机交互和信息理解的新境界。它超越了单一感官输入的限制,通过整合视觉、听觉、文本等多种数据类型,构建了一个更加丰富、立体的认知模型,为机器赋予了接近人类的综合感知与理解能力。本文将深入探讨多模态机器学习的定义、核心原理、关键技术、面临的挑战以及未来的应用前景,旨在为读者勾勒出这一
- 谷歌吹响反击号角:2025年Gemini用户目标5亿,AI大战一触即发!
that's boy
人工智能chatgptopenaiAI工具AI编程googlegemini
人工智能领域的竞争日趋白热化,谷歌CEO桑达·皮采亲自下场,为GeminiAI定下了雄心勃勃的目标:到2025年底,用户突破5亿!面对ChatGPT的强势崛起,谷歌能否成功逆袭?本文将深入剖析谷歌的战略布局、Gemini的技术优势以及未来AI竞争的格局。谷歌的反击:5亿用户的雄心壮志在过去几年,OpenAI凭借ChatGPT的强大实力,几乎垄断了AI领域的聚光灯。谷歌虽然在AI技术研究方面一直处于
- 逆袭之路(11)——python网络爬虫:原理、应用、风险与应对策略
凋零的蓝色玫瑰
逆袭之路php开发语言python
困厄铸剑心,逆袭展锋芒。寒苦凝壮志,腾跃绘华章。我要逆袭。目录一、引言二、网络爬虫的基本原理(一)网络请求与响应(二)网页解析(三)爬行策略三、网络爬虫的应用领域(一)搜索引擎(二)数据挖掘与分析(三)金融领域(四)学术研究(五)社交媒体监测四、网络爬虫带来的风险(一)法律风险(二)隐私风险(三)安全风险五、网络爬虫风险的应对策略(一)遵守法律法规(二)加强技术防护(三)提高道德意识六、结论一、引
- Python小游戏28——水果忍者
虞书欣的C
游戏pycharm人工智能小程序开发语言
首先,你需要安装Pygame库。如果你还没有安装,可以使用以下命令进行安装:【bash】pipinstallpygame《水果忍者》游戏代码:【python】importpygameimportrandomimportsys#初始化Pygamepygame.init()#设置屏幕尺寸screen_width=800screen_height=600screen=pygame.display.set
- 如何用Python爬取网站数据:基础教程与实战
大梦百万秋
知识学爆python开发语言
数据爬取(WebScraping)是从网站中自动获取信息的过程。借助Python强大的库和工具,数据爬取变得非常简单且高效。本文将介绍Python爬取网站数据的基础知识、常用工具,以及一个简单的实战示例,帮助你快速上手网站数据爬取。1.什么是网站数据爬取?网站数据爬取是通过编写程序自动抓取网页内容的技术,通常用于从公开网站中提取特定数据。数据爬取的应用场景非常广泛,包括:收集商品价格和评论数据新闻
- python实现滑雪游戏
是叶子耶
pygamepython开发语言
游戏逻辑说明初始化:设置游戏窗口、颜色、滑雪者和障碍物的基本属性。绘制窗口:在每一帧中绘制滑雪者、障碍物和当前得分。用户输入:通过键盘的左右箭头控制滑雪者的移动。障碍物生成和移动:随机生成障碍物,并使其向下移动。碰撞检测:检查滑雪者是否与任何障碍物碰撞,若碰撞则结束游戏。得分系统:每一帧增加得分。importpygameimportrandom#初始化pygamepygame.init()#游戏窗
- AI大模型引领医疗变革:十大创新应用场景塑造智慧医疗新时代
和老莫一起学AI
人工智能自动化数据库学习语言模型大模型
前言在人工智能技术的迅猛发展中,AI大模型以其无与伦比的数据处理能力和深度学习能力,正逐步成为医疗健康领域变革的引领者。本文旨在深入探讨AI大模型在医疗领域的十大创新应用场景,展示其如何显著提升医疗服务效率、赋能临床决策,并推动整个行业向智能化转型。一、智能化诊疗:精准辅助,提升诊断效率AI大模型凭借对海量医疗数据的深度分析,能够协助医生进行更为精准的诊断。例如,百度灵医大模型凭借强大的数据处理能
- 如何抓取社交媒体上的公开用户信息:完整的Python爬虫教程与实战
Python爬虫项目
媒体python爬虫selenium开发语言ajax
引言社交媒体平台如Twitter、Instagram、Facebook和LinkedIn等,成为了现代社会中获取信息、表达观点、社交互动的主要场所。通过社交媒体,用户分享个人信息、兴趣、活动以及与他人的互动数据,极大地丰富了网络世界的内容。在数据分析、市场研究、舆情监控等领域,抓取社交媒体上的公开用户信息是非常重要的任务。对于很多数据科学家、市场分析师、爬虫开发者来说,如何高效地抓取社交媒体平台的
- 基于Python的股市数据爬取与分析:从实时行情到历史数据的完整教程
Python爬虫项目
2025年爬虫实战项目python数据挖掘开发语言爬虫oracle人工智能
引言股市投资是一项具有高度风险和回报的活动,实时行情和历史数据的获取是股市分析和决策的基础。随着数据科学和爬虫技术的迅速发展,许多投资者和分析师通过编写Python爬虫来获取股市数据,进行数据分析、技术分析和预测。无论是获取实时股市行情,还是分析股票的历史数据,Python都能为我们提供强大的工具支持。本篇博客将为你提供一个完整的股市数据爬取与分析教程,介绍如何利用Python爬虫获取实时股市行情
- Python爬虫教程:抓取区块链交易信息及加密货币市场数据
Python爬虫项目
2025年爬虫实战项目python爬虫区块链开发语言人工智能网络爬虫
前言随着区块链技术和加密货币的迅猛发展,区块链交易和加密货币市场的数据逐渐成为金融、技术、经济研究等领域的热点。对于开发者和研究者而言,实时获取区块链交易数据和加密货币市场行情,对于投资分析、市场预测、技术研究等具有重要的参考价值。本文将通过Python爬虫技术,介绍如何抓取区块链交易信息及加密货币市场数据,详细阐述数据获取的原理、技术方案、实现方法以及抓取到的数据的存储与分析。我们将依托最新的爬
- Python 爬虫:商品价格监控与波动分析
Python爬虫项目
2025年爬虫实战项目python爬虫开发语言ide网络爬虫
随着电子商务的迅猛发展,商品价格的监控和波动分析在各类应用中具有重要价值。通过爬取电商平台的商品价格数据,我们不仅可以分析商品的价格趋势,还可以预测未来的价格波动,并为定价、促销策略提供数据支持。本文将详细介绍如何利用Python编写爬虫,抓取商品价格数据,并进行价格波动分析。目录1.爬虫概述与技术选型2.环境配置与依赖库安装3.目标平台与数据抓取3.1获取商品价格示例:抓取京东商品价格3.2抓取
- python爬虫 短视频平台数据抓取:抓取视频和评论
Python爬虫项目
2025年爬虫实战项目python爬虫音视频网络爬虫开发语言
随着短视频平台如抖音、快手、TikTok等的兴起,越来越多的内容创作者和观众通过短视频平台分享和观看视频内容。短视频平台包含了丰富的数据,如视频内容、评论、点赞数、分享数等,这些数据对市场分析、用户行为分析、视频推荐算法等方面具有重要意义。抓取这些数据可以帮助我们获取平台的动态信息,为数据分析提供基础。本文将详细介绍如何使用Python编写爬虫抓取短视频平台上的视频和评论数据,包括技术栈选择、爬虫
- Delphi代码编写标准指南
好大的牛角
分享一下我老师大神的人工智能教程!零基础,通俗易懂!http://blog.csdn.net/jiangjunshow也欢迎大家转载本篇文章。分享知识,造福人民,实现我们中华民族伟大复兴!·日月光华精华区文章阅读发信人:Delphii(Delphi),信区:VCL标题:Delphi编码规则发信站:日月光华站(FriSep712:03:072001),站内信件Delphi代码编写标准指南■■■■■■
- Python 常用基础模块(三):os.path模块
Amo Xiang
Python3高级核心技术python开发语言
目录一、os.path模块介绍二、常用方法2.1exists()方法——判断路径是否存在(准确)2.2isdir()方法——判断是否为目录2.3isabs()方法——判断是否为绝对路径2.4isf ile()方法——判断是否为普通文件2.5join()方法——拼接路径2.6abspath()方法——获取绝对路径2.7basename()方法——从一个路径中提取文件名2.8dirname()方法——
- Python字典实战:打造高效学生成绩管理系统
清水白石008
pythonPython题库python开发语言
Python字典实战:打造高效学生成绩管理系统在日常学习和工作中,我们经常需要管理和查询数据。Python的字典(Dictionary)是一种非常强大的数据结构,它以键值对(key-valuepairs)的形式存储数据,能够实现高效的数据检索。本文将以创建一个学生成绩管理系统为例,深入讲解如何使用Python字典存储学生姓名和成绩信息,并实现根据姓名查找成绩的功能。本文旨在提供实用性强、内容丰富、
- html页面js获取参数值
0624chenhong
html
1.js获取参数值js
function GetQueryString(name)
{
var reg = new RegExp("(^|&)"+ name +"=([^&]*)(&|$)");
var r = windo
- MongoDB 在多线程高并发下的问题
BigCat2013
mongodbDB高并发重复数据
最近项目用到 MongoDB , 主要是一些读取数据及改状态位的操作. 因为是结合了最近流行的 Storm进行大数据的分析处理,并将分析结果插入Vertica数据库,所以在多线程高并发的情境下, 会发现 Vertica 数据库中有部分重复的数据. 这到底是什么原因导致的呢?笔者开始也是一筹莫 展,重复去看 MongoDB 的 API , 终于有了新发现 :
com.mongodb.DB 这个类有
- c++ 用类模版实现链表(c++语言程序设计第四版示例代码)
CrazyMizzz
数据结构C++
#include<iostream>
#include<cassert>
using namespace std;
template<class T>
class Node
{
private:
Node<T> * next;
public:
T data;
- 最近情况
麦田的设计者
感慨考试生活
在五月黄梅天的岁月里,一年两次的软考又要开始了。到目前为止,我已经考了多达三次的软考,最后的结果就是通过了初级考试(程序员)。人啊,就是不满足,考了初级就希望考中级,于是,这学期我就报考了中级,明天就要考试。感觉机会不大,期待奇迹发生吧。这个学期忙于练车,写项目,反正最后是一团糟。后天还要考试科目二。这个星期真的是很艰难的一周,希望能快点度过。
- linux系统中用pkill踢出在线登录用户
被触发
linux
由于linux服务器允许多用户登录,公司很多人知道密码,工作造成一定的障碍所以需要有时踢出指定的用户
1/#who 查出当前有那些终端登录(用 w 命令更详细)
# who
root pts/0 2010-10-28 09:36 (192
- 仿QQ聊天第二版
肆无忌惮_
qq
在第一版之上的改进内容:
第一版链接:
http://479001499.iteye.com/admin/blogs/2100893
用map存起来号码对应的聊天窗口对象,解决私聊的时候所有消息发到一个窗口的问题.
增加ViewInfo类,这个是信息预览的窗口,如果是自己的信息,则可以进行编辑.
信息修改后上传至服务器再告诉所有用户,自己的窗口
- java读取配置文件
知了ing
1,java读取.properties配置文件
InputStream in;
try {
in = test.class.getClassLoader().getResourceAsStream("config/ipnetOracle.properties");//配置文件的路径
Properties p = new Properties()
- __attribute__ 你知多少?
矮蛋蛋
C++gcc
原文地址:
http://www.cnblogs.com/astwish/p/3460618.html
GNU C 的一大特色就是__attribute__ 机制。__attribute__ 可以设置函数属性(Function Attribute )、变量属性(Variable Attribute )和类型属性(Type Attribute )。
__attribute__ 书写特征是:
- jsoup使用笔记
alleni123
java爬虫JSoup
<dependency>
<groupId>org.jsoup</groupId>
<artifactId>jsoup</artifactId>
<version>1.7.3</version>
</dependency>
2014/08/28
今天遇到这种形式,
- JAVA中的集合 Collectio 和Map的简单使用及方法
百合不是茶
listmapset
List ,set ,map的使用方法和区别
java容器类类库的用途是保存对象,并将其分为两个概念:
Collection集合:一个独立的序列,这些序列都服从一条或多条规则;List必须按顺序保存元素 ,set不能重复元素;Queue按照排队规则来确定对象产生的顺序(通常与他们被插入的
- 杀LINUX的JOB进程
bijian1013
linuxunix
今天发现数据库一个JOB一直在执行,都执行了好几个小时还在执行,所以想办法给删除掉
系统环境:
ORACLE 10G
Linux操作系统
操作步骤如下:
第一步.查询出来那个job在运行,找个对应的SID字段
select * from dba_jobs_running--找到job对应的sid
&n
- Spring AOP详解
bijian1013
javaspringAOP
最近项目中遇到了以下几点需求,仔细思考之后,觉得采用AOP来解决。一方面是为了以更加灵活的方式来解决问题,另一方面是借此机会深入学习Spring AOP相关的内容。例如,以下需求不用AOP肯定也能解决,至于是否牵强附会,仁者见仁智者见智。
1.对部分函数的调用进行日志记录,用于观察特定问题在运行过程中的函数调用
- [Gson六]Gson类型适配器(TypeAdapter)
bit1129
Adapter
TypeAdapter的使用动机
Gson在序列化和反序列化时,默认情况下,是按照POJO类的字段属性名和JSON串键进行一一映射匹配,然后把JSON串的键对应的值转换成POJO相同字段对应的值,反之亦然,在这个过程中有一个JSON串Key对应的Value和对象之间如何转换(序列化/反序列化)的问题。
以Date为例,在序列化和反序列化时,Gson默认使用java.
- 【spark八十七】给定Driver Program, 如何判断哪些代码在Driver运行,哪些代码在Worker上执行
bit1129
driver
Driver Program是用户编写的提交给Spark集群执行的application,它包含两部分
作为驱动: Driver与Master、Worker协作完成application进程的启动、DAG划分、计算任务封装、计算任务分发到各个计算节点(Worker)、计算资源的分配等。
计算逻辑本身,当计算任务在Worker执行时,执行计算逻辑完成application的计算任务
- nginx 经验总结
ronin47
nginx 总结
深感nginx的强大,只学了皮毛,把学下的记录。
获取Header 信息,一般是以$http_XX(XX是小写)
获取body,通过接口,再展开,根据K取V
获取uri,以$arg_XX
&n
- 轩辕互动-1.求三个整数中第二大的数2.整型数组的平衡点
bylijinnan
数组
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class ExoWeb {
public static void main(String[] args) {
ExoWeb ew=new ExoWeb();
System.out.pri
- Netty源码学习-Java-NIO-Reactor
bylijinnan
java多线程netty
Netty里面采用了NIO-based Reactor Pattern
了解这个模式对学习Netty非常有帮助
参考以下两篇文章:
http://jeewanthad.blogspot.com/2013/02/reactor-pattern-explained-part-1.html
http://gee.cs.oswego.edu/dl/cpjslides/nio.pdf
- AOP通俗理解
cngolon
springAOP
1.我所知道的aop 初看aop,上来就是一大堆术语,而且还有个拉风的名字,面向切面编程,都说是OOP的一种有益补充等等。一下子让你不知所措,心想着:怪不得很多人都和 我说aop多难多难。当我看进去以后,我才发现:它就是一些java基础上的朴实无华的应用,包括ioc,包括许许多多这样的名词,都是万变不离其宗而 已。 2.为什么用aop&nb
- cursor variable 实例
ctrain
variable
create or replace procedure proc_test01
as
type emp_row is record(
empno emp.empno%type,
ename emp.ename%type,
job emp.job%type,
mgr emp.mgr%type,
hiberdate emp.hiredate%type,
sal emp.sal%t
- shell报bash: service: command not found解决方法
daizj
linuxshellservicejps
今天在执行一个脚本时,本来是想在脚本中启动hdfs和hive等程序,可以在执行到service hive-server start等启动服务的命令时会报错,最终解决方法记录一下:
脚本报错如下:
./olap_quick_intall.sh: line 57: service: command not found
./olap_quick_intall.sh: line 59
- 40个迹象表明你还是PHP菜鸟
dcj3sjt126com
设计模式PHP正则表达式oop
你是PHP菜鸟,如果你:1. 不会利用如phpDoc 这样的工具来恰当地注释你的代码2. 对优秀的集成开发环境如Zend Studio 或Eclipse PDT 视而不见3. 从未用过任何形式的版本控制系统,如Subclipse4. 不采用某种编码与命名标准 ,以及通用约定,不能在项目开发周期里贯彻落实5. 不使用统一开发方式6. 不转换(或)也不验证某些输入或SQL查询串(译注:参考PHP相关函
- Android逐帧动画的实现
dcj3sjt126com
android
一、代码实现:
private ImageView iv;
private AnimationDrawable ad;
@Override
protected void onCreate(Bundle savedInstanceState)
{
super.onCreate(savedInstanceState);
setContentView(R.layout
- java远程调用linux的命令或者脚本
eksliang
linuxganymed-ssh2
转载请出自出处:
http://eksliang.iteye.com/blog/2105862
Java通过SSH2协议执行远程Shell脚本(ganymed-ssh2-build210.jar)
使用步骤如下:
1.导包
官网下载:
http://www.ganymed.ethz.ch/ssh2/
ma
- adb端口被占用问题
gqdy365
adb
最近重新安装的电脑,配置了新环境,老是出现:
adb server is out of date. killing...
ADB server didn't ACK
* failed to start daemon *
百度了一下,说是端口被占用,我开个eclipse,然后打开cmd,就提示这个,很烦人。
一个比较彻底的解决办法就是修改
- ASP.NET使用FileUpload上传文件
hvt
.netC#hovertreeasp.netwebform
前台代码:
<asp:FileUpload ID="fuKeleyi" runat="server" />
<asp:Button ID="BtnUp" runat="server" onclick="BtnUp_Click" Text="上 传" />
- 代码之谜(四)- 浮点数(从惊讶到思考)
justjavac
浮点数精度代码之谜IEEE
在『代码之谜』系列的前几篇文章中,很多次出现了浮点数。 浮点数在很多编程语言中被称为简单数据类型,其实,浮点数比起那些复杂数据类型(比如字符串)来说, 一点都不简单。
单单是说明 IEEE浮点数 就可以写一本书了,我将用几篇博文来简单的说说我所理解的浮点数,算是抛砖引玉吧。 一次面试
记得多年前我招聘 Java 程序员时的一次关于浮点数、二分法、编码的面试, 多年以后,他已经称为了一名很出色的
- 数据结构随记_1
lx.asymmetric
数据结构笔记
第一章
1.数据结构包括数据的
逻辑结构、数据的物理/存储结构和数据的逻辑关系这三个方面的内容。 2.数据的存储结构可用四种基本的存储方法表示,它们分别是
顺序存储、链式存储 、索引存储 和 散列存储。 3.数据运算最常用的有五种,分别是
查找/检索、排序、插入、删除、修改。 4.算法主要有以下五个特性:
输入、输出、可行性、确定性和有穷性。 5.算法分析的
- linux的会话和进程组
网络接口
linux
会话: 一个或多个进程组。起于用户登录,终止于用户退出。此期间所有进程都属于这个会话期。会话首进程:调用setsid创建会话的进程1.规定组长进程不能调用setsid,因为调用setsid后,调用进程会成为新的进程组的组长进程.如何保证? 先调用fork,然后终止父进程,此时由于子进程的进程组ID为父进程的进程组ID,而子进程的ID是重新分配的,所以保证子进程不会是进程组长,从而子进程可以调用se
- 二维数组 元素的连续求解
1140566087
二维数组ACM
import java.util.HashMap;
public class Title {
public static void main(String[] args){
f();
}
// 二位数组的应用
//12、二维数组中,哪一行或哪一列的连续存放的0的个数最多,是几个0。注意,是“连续”。
public static void f(){
- 也谈什么时候Java比C++快
windshome
javaC++
刚打开iteye就看到这个标题“Java什么时候比C++快”,觉得很好笑。
你要比,就比同等水平的基础上的相比,笨蛋写得C代码和C++代码,去和高手写的Java代码比效率,有什么意义呢?
我是写密码算法的,深刻知道算法C和C++实现和Java实现之间的效率差,甚至也比对过C代码和汇编代码的效率差,计算机是个死的东西,再怎么优化,Java也就是和C