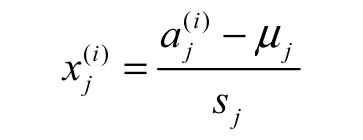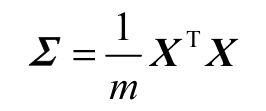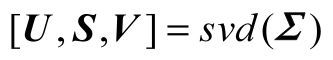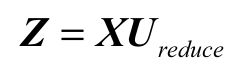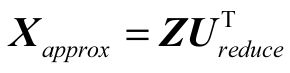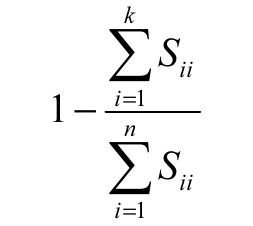机器学习之PCA算法
PCA 是 Principal Component Analysis 的缩写,中文称为主成分分析法。它是一种维数约减(Dimensionality Reduction)算法,即把高维度数据在损失最小的情况下转换为低维度数据的算法。显然,PCA 可以用来对数据进行压缩,可以在可控的失真范围内提高运算速度,提高机器学习的效率,使较为复杂的数据简单化。
所谓损失最小就是从高维向低维映射的时候误差最小,低位空间的描述是向量组,k维空间就用k个向量来描述这个空间。
假设有一个数据集,用 m×n 维的矩阵 A 表示。矩阵中每一行表示一个样本,每一列表示一个特征,总共有 m 个样本,每个样本有 n 个特征。我们的目标是减少特征个数,只保留最重要的 k 个特征。
为了简化计算,采取数据归一化和缩放,归一化是使样本的均值为0,缩放是为了把所有的值都控制在-1到1的区间内
X是归一化和缩放后的数据,a是原数据,u是数据的均值,s是极差
sigma表示协方差矩阵,由X矩阵及其转置矩阵相乘再除以矩阵X的行数
n*m的矩阵乘以m*n的矩阵结果是一个n*n的矩阵
接着通过奇异值分解来计算协方差矩阵的特征向量(eigenvectors):
svd是奇异值运算,这个东西我也不太懂,上网查一查去
好吧,还是看不太懂,等我懂了再来更新
通过上面这个就可以算出特征矩阵
然后对特征矩阵进行降维处理,下面的这个公式Z是降维之后得到的矩阵,U是从上面奇异值分解得来的,但是只取前k个向量作为Ureduce,之前的U向量是n*n,现在变为n*k,X是数据归一化和缩放后的数据矩阵m*n
此时z的大小是m*k实现了降维,因为k一定是小于n的
另外矩阵既然有降维也就会有还原,下面是还原的公式,只是上面公式的变形
下面是python代码实现PCA算法,主要用到numpy和scikit-learn
import numpy as np
A = np.array([[3,2000],
[2,3000],
[4,5000],
[5,8000],
[1,2000]],dtype='float')
mean = np.mean(A,axis=0)
norm = A - mean//数据归一化
scope = np.max(norm,axis=0) - np.min(norm,axis=0)//极差
norm = norm / scope//缩放
norm
U, S, V = np.linalg.svd(np.dot(norm.T,norm))//奇异值分解
U
U_reduce = U[:,0].reshape(2,1)//Ureduce矩阵
U_reduce
R = np.dot(norm,U_reduce)//降维计算
R
Z = np.dot(R,U_reduce.T)//还原
Z
np.multiply(Z,scope) + mean//缩放和归一化的逆预算
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import MinMaxScaler
def std_PCA(**argv):
scaler = MinMaxScaler()//数据预处理
pca = PCA(**argv)//PCA算法
pipeline = Pipeline([('scaler',scaler),
('pca',pca)])//用管道链接
return pipeline
pca = std_PCA(n_components=1)
R2 = pca.fit_transform(A)
R2
pca.inverse_transform(R2)数据还原率
Xapprox为还原后的数据,所谓的数据还原只不过是将已经降维的坐标还原到原来的坐标系中,不可避免的会产生误差,
所以我们需要指标来衡量这一误差是否在我们能接受的范围内
在寻找最有的k时,k是Ureduce的n*k阶矩阵,k从1开始不断增长,所以是一个迭代的过程,需要多次条用PCA,效率低下
实际计算时会选用下面的公式
只需要一次调用就可以解决问题