密码学实验 | shamir门限秘密共享算法（python）

一、实验原理

(t，n)门限秘密共享方案，该方案是Shamir和Blakley在1979年各自独立地提出。

(t，n)门限方案是基于(t.n)门限访问结构上的秘密共享方案，而(t，n)门限访问结构包括所有t个或t个以上的参与者子集所构成的集合。

1. Shamir (t，n)门限方案是通过构造一个t-1次多项式，并将需共享的秘密作为该多项式的常数项，将秘密分成n部分分别给n个参与者，使t个参与者联合可恢复秘密，但少于t个参与者联合不能得到共享秘密的任何信息。Blakley独立地提出的另一个(t，n)门限方案，它的基本思想是利用多维空间中的点来建立门限方案，将共享的秘密看成t维空间中的一个点，每个子秘密为包含这个点的t-1维超平面的方程，任意t个t- 1维超平面的交点刚好确定共享的秘密，而t-1个子秘密(即t-1个t-1维超平面)仅能确定其交线，因而得不到共享秘密的任何信息。

2. Blakley方案比Shamir方案信息率低，但它有一个特殊的性质:任意t个子秘密除确定交点以外，它们相互之间是无关的，而Shamir方案却与此不同，任意t个子秘密能够确定整个多项式，并能计算出其余参与者的子秘密。

二、实验代码

# -*- coding:utf-8 -*- 
import random
import math


"""
This program generates a Shamir (t,n)-Threshold Scheme, with the desired
settings - as set by the user. The scheme can be initiated by running this
python script through the command line, or run directly via the python shell.

For specifications, the program requires the following 4 parameters:
-Prime field, over which all calculations will be conducted
-Desired secret, in the form of some number less than the prime field
-Number of total participants
-Size of threshold
"""

# 输入q, n, t, k 
def initiateScheme(predefinedVars):
    kField = []
    n = 0
    t = 0
    #*Allows scheme to be run multiple times with different secret
    if not predefinedVars:
        Elements = input("Enter prime field (q)\n")

        q = int(Elements)
        q = testPrimality(q)
        
        Field = createField(q)
        print("\nField created:")
        print("q:", Field)

        kField = Field
        
        n = input("Enter number of participants n (less than field order)\n")
        t = input("Enter access structure length t (less than participant number)\n")
        
        predefinedVars = [n, t, q, Field]
        
        if(n >= t):
            print("Creating new (" + t + ", " + n + ")-Threshold Scheme")
        
        else:
            print("Access structure length must be less than number of participants")
            initiateScheme()
    else:
        kField = predefinedVars[3]
        q = predefinedVars[2]
        t = predefinedVars[1]
        n = predefinedVars[0]
    
    secretInd = input("\nEnter index of desired secret (k) in field (0 to (q-1))\n")
    secret_k = kField[int(secretInd)]
    print("k:", secret_k)

    recovered_k = runScheme(t, n, secret_k, q, Field)
    
    return predefinedVars, recovered_k

# 检查是不是素数
def testPrimality(q):
    i = q
    q = math.sqrt(q)
    q = int(q)
    for p in range(2, (q+1)):
        f = i / p
        if(f.is_integer()):
            #print(f)
            #print(i)
            #print(p)
            newQ = input("Enter prime number")
            newQ = int(newQ)
            newQ = testPrimality(newQ)
            i = newQ
            break
    return i

# 创建有限域 GF(q)
def createField(q):
    ModuloK = []
    for i in range(0, q):
        ModuloK.append(i) 
    
    return ModuloK
    
# 运行算法
def runScheme(t_str, n_str, k, q, Field):
    x_subi = [0]
    a_subj = [0]
    pShares = [0]
    pShares_regex = [0]
    
    t = int(t_str)
    n = int(n_str)
    
    for i in range(1, n+1):
        #print("ran")
        x = getDistinctX(x_subi, Field)
        x_subi.append(x)

    print("x 所有取值:", x_subi)
    
    for j in range(1, t):
        ind = random.randint(0, q)
        a_subj.append(Field[ind])
    # 根据需要加减a_i的值
    print("a_1的值:", a_subj[1], "a_2的值:", a_subj[2])
    print("a_3的值:", a_subj[3], "a_4的值:", a_subj[4])    

    
    for i in range(1, n+1):
        x = x_subi[i]
        # print("x_i的值:",x)
        polynomialSum = k
        #print(k)
        for j in range(1, t):
            a = a_subj[j]
            # print("a:", a)
            exponent = math.pow(x, j)
            # print("exponent:", exponent)
            polynomialSum += a * exponent
            # print("polynomialSum:", polynomialSum)
        
        regEx = polynomialSum % q
        print("(%d, %d)" %(x, regEx))
        pShares_regex.append(regEx)
        # print("all f(x) :", pShares_regex)
        
        pShares.append(polynomialSum)

    # 根据你需要的多项式，手动修改
    # print("f(x) = %d + %d x +%d x^2  mod %d" %(k, a_subj[1], a_subj[2], q))
    print("f(x) = %d + %d x +%d x^2 +%d x^3 + %d x^4 mod %d" %(k, a_subj[1], a_subj[2], a_subj[3], a_subj[4] ,q))
    print("Shares generated")
    displayShares_i(pShares_regex)


    generatedK = tryAccessStructure(k, pShares, x_subi, t_str, q)
    
    return generatedK


def reduce(integer, F):
    F.sort(reverse=True)
    print(F)
    binary = []
    regEx = []
    for i, f in enumerate(F):
        if(integer >= f):
            integer -= f

            binary.append(1)
            regEx.append(f)
        else:
            binary.append(0)

    return binary, regEx


def tryAccessStructure(k, pShares, x_subi, t_str, q):
    P_Subset = getSubset()

    generatedK = generateK(pShares, x_subi, P_Subset, q)
    if(generatedK != k):
        print("Incorrect secret; access structure must be of length: " + t_str)
    else:
        print("Secret recovered")
    r = input("Try different access structure (Y or N)\n")
    if(r.upper() == "Y"):
        generatedK = tryAccessStructure(k, pShares, x_subi, t_str, q)

    return generatedK

# 生成x的值，x = 1~5
def getDistinctX(x_subi, F): 
    #x_subi = []
    ind = random.randint(1, 5)
    # ind = range(0, (len(F)-1))
    x = F[ind]
    if not x in x_subi:
        return x
    else:
        x = getDistinctX(x_subi, F)
        return x

    

def displayShares_i(pShares):
    P_ID_str = input("Enter participant number to see share (number from 1 - n)\n")
    P_ID = int(P_ID_str)
    try:
        Share = pShares[P_ID]
        Share = int(Share)
        print("Share for participant #" + P_ID_str + ": " + str(Share))
        Repeat = input("Display another share (Y, or N)\n")
        if(Repeat.upper() == "Y"):
            displayShares_i(pShares)
    except:
        print("Index out of range: \nEnter number between 1 and access structure length.")
        displayShares_i(pShares)
    
    return 

# 获取子密钥
def getSubset():
    Subset_RAWstr = input("\nEnter list of participants who wish to recover the secret\nEnter in form 'ID#1 ID#2 ... ID#T' where ID#i is the number of\nparticipant i \n")
    Subset_str = Subset_RAWstr.split()
    Subset = [0]
    Subset_mm = input("Enter list of Participant i secrets\n")
    for ID in Subset_str:
        try:
            ID = int(ID)
            Subset.append(ID)
        except:
            print("Error in list entered, try again")
            Subset = getSubset()
            #ADD RECURSIVE FUNCTION
        
    return Subset

# 恢复秘密k 
def generateK(pShares, x_subi, Subset, q):
    y_subset = []
    x_subset = []
    
    Subset.sort()
    for ID in Subset:
        y_i = pShares[ID]
        x_i = x_subi[ID]
        y_subset.append(y_i)
        x_subset.append(x_i)
    
    recoveredK = 0
    for j in range(1, (len(x_subset))):
        x_j = x_subset[j]
        b_j = 1
        for L in range(1, len(x_subset)):
            if(L != j):
                x_L = x_subset[L]
                newCoeff = float(x_L)/(x_L - x_j)
                b_j = b_j * newCoeff
        recoveredK += y_subset[j] * (b_j)

    recoveredK_int = int(round(recoveredK))
    print("恢复出的秘密值k：", recoveredK_int)
    
    return recoveredK_int


def runPackage(predefinedVars, recoveredKs):
    predefinedVars, returnK = initiateScheme(predefinedVars)
    # print("predefinedVars:", predefinedVars, "returnK:", returnK)
    if returnK in predefinedVars:
        print("New secret found:" + str(returnK))
        recoveredKs.append(returnK)
        print(recoveredKs)
    else:
        print("Invalid access structure")

    response = input("Run process again for different k in field (Y or N).\n")
    if(response.upper() == "Y"):
        runPackage(predefinedVars, recoveredKs)
    
# initiateScheme()

runPackage([], [])

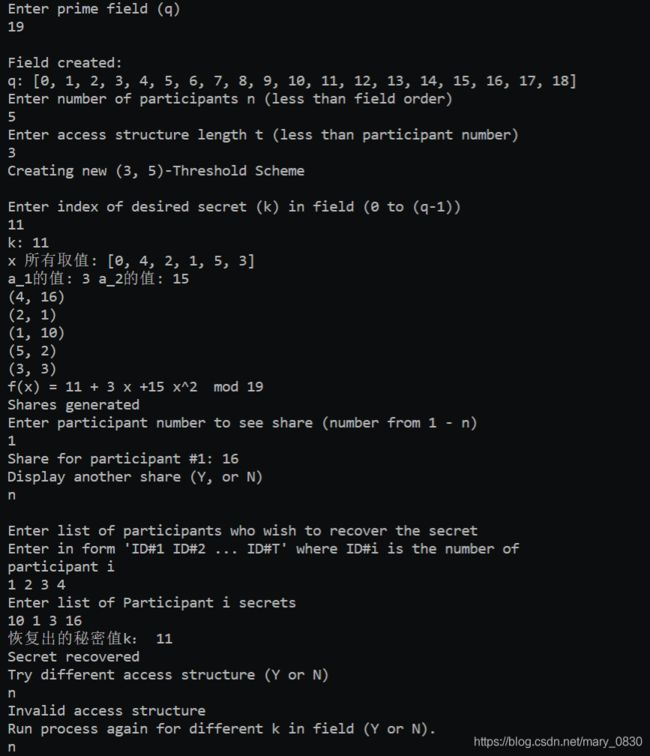
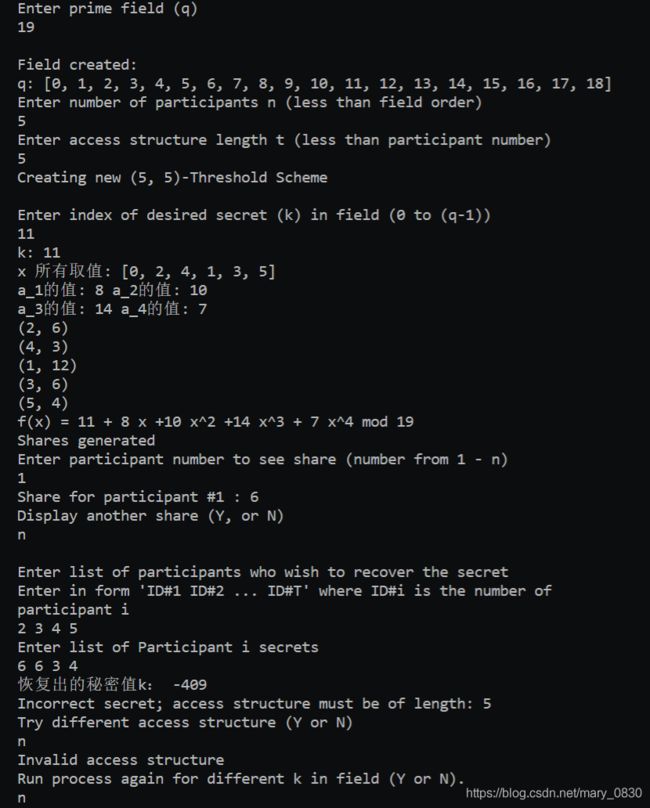
三、实验结果

解密正确：

解密错误：

四、实验总结

在这次实验中，使用的是python编写shamir门限算法，通过构造初始化函数、创建有限域 GF(q)、运行算法等函数组合编写成该门限共享方案。
通过这次实验，可以知道秘密共享算法是一种非常安全的算法，将共享的秘密分成若干份分别给予若干参与者保管，并规定哪些参与者联合起来可重构秘密，哪些参与者联合起来并不能得到任何信息，就像示例3所示，当参与者个数少于最少重构秘密个数时，则不能得到任何信息。