Ouroboros：A Provably Secure Proof-of-Stake Blockchain Protocol 学习总结

        Ouroboros首次在论文《Ouroboros：A Provably Secure Proof-of-Stake Blockchain Protocol 》中提出，中文名称是乌洛波洛斯，它ADA项目的共识算法，由卡尔达诺(Cardano)团队设计开发，这个共识机制呢，以严谨的学术性以及发表在顶级密码学会议上而闻名，是第一个被工业界采用的 学术界证明是安全和健壮的POS算法。

• 常见共识机制

      首先总结一下目前的共识机制，主要有三类：分别是：

      ·工作量证明（PoW，Proof of Work）

      ·权益证明（PoS，Proof of Stake）

     · 股份授权证明（DPoS，Delegated proof of stake）

      POW是算力竞赛，设计一个计算哈希的难题，谁先算出来谁胜出，算力越高胜出的概率越高，以这样的方式保证胜出者是随机的，并且易于验证。POS是选举，根据区块链中账户拥有权益的比例，随机投票选举出块人，拥有的权益越大，那么成为下一个区块生产者的概率也越大。需要在非常多的节点之间达成一致，这对一致性验证、防伪的要求比较高，为了解决POS达成一致效率低以及无利益攻击的问题，DPOS做了一些改进，与POS的主要区别在于节点选举若干代理人，由代理人验证和记账。这种机制有些偏于中心化，但极大地提高了共识和出块效率。

     本质上，POW和POS都是一种随机选择区块记账者的方式，为了确保区块链的安全性，POS协议选举记账者的方法必须是随机的。为了实现选举（Leader election）过程的随机性，IOHK首席科学家Aggelos Kiayias教授领导的团队设计了Ouroboros共识机制。它是第一个具有严谨数学证明安全性的权益证明协议，该协议的目的是根据权益大小随机选出一个记账者，并且这个过程是不可预测的，从而不会产生恶意攻击。 下面就开始详细介绍Ouroboros共识机制。

• 术语解释

        首先解释一些常用的术语：

        在这个共识机制中，时间被分为slot，每个slot只能产生一个块，如果这个块有问题，或者应该产出这个块的“矿工”不在线，或者产出的块没有广播给大多数人，那么这个slot是当作废弃的，也就是会跳过这个slot的块。

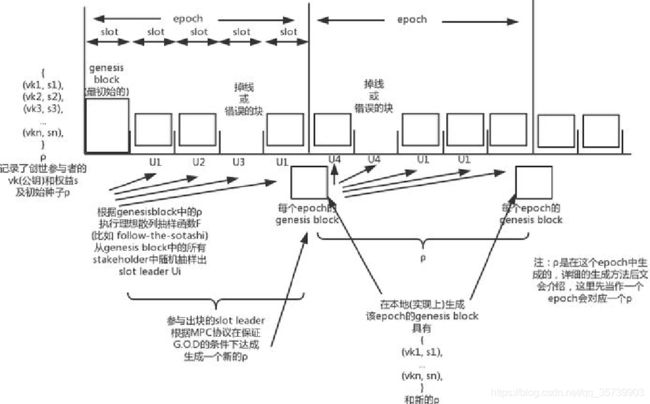
        多个slot组成一个epoch，每个epoch的开头有个初始块(注意是每一个epoch，不是整个链)，这个初始块不会上链，而是当前这个节点自己在内存中生成，这个初始块会记录当前这个epoch中的可能参与出块的stakeholder的候选人，以及一个随机种子ρ。

        stakeholder是权益持有者，也就是潜在矿工，要成为一个权益持有者需要有2%的Ada才行。而stakeholder并不一定要参与出块，只有记录在每个epoch初始块中的stakeholder，它才能参与当前epoch中某个slot的出块，这些stakeholder叫做 “stakeholder候选人”，也就是说epoch中，每个slot的区块打包者，都是在这些stakeholder候选人中选举出来的。

       每个epoch结束之后，由这些epoch衔接而成的链就是由共识产生的链，这个链的基本属性和Bitcoin大致相同(如每个块包含上一个块的hash等等)。

• Ouroboros总体运行流程

       在这些术语的基础上，结合上图介绍一下的这个共识机制的工作流程:

       首先，第一个步骤，从链的真正创世块开始，产生相应的公钥和这些公钥对应的权益s，还有初始的随机种子ρ，之后，这个epoch会采用这些基础信息继续运行。

       然后，第二个步骤，每个节点独立的运行代码，根据当前epoch的随机种子ρ，执行散列抽样函数F，把初始块中的权益s，随机种子ρ和slot的index作为输入，根据权益占比的概率来获得当前这个slot应该由谁出块。 这个函数后面会详细介绍，现在就把他理解为一个黑匣子，功能是选出每个slot的出块者。

        在某个slot中，

     （1）如果发现是自己出块，那么就执行打包交易的操作，和比特币没有太大区别。除了基础工作之外，还会生成一个随机数，这个后面会用到。

     （2）如果不是自己出块，那么等待出块者出块并广播。收到这个块的时候就进行和比特币类似的检查，如果长时间未收到(也就是超出这个slot的时间没有收到块的广播)就会丢弃这个slot的块。

        最后，第三个步骤，在当前epoch中不断重复步骤2直到所有slot结束。 在整个epoch的过程中会产出一个出块者们都认同的随机种子ρ。参与共识的节点在本地记录好这个ρ及参与下一个epoch选举的stakeholder，开启一个新的周期。这样就完成一个epoch，然后由每个epoch产生的块衔接成链。

         这就是 Ouroboros共识机制 大致执行的流程。

• 关键问题

       根据刚才所描述的的流程，再结合这个共识机制目的是“随机选出记账者”，那么关键问题：如何随机的选出记账者呢？

       在这个共识机制中，由于epoch模型，这个问题被分成两个部分：

       第一个是，产生一个随机种子ρ 。

       第二个是，根据随机种子ρ，在当前epoch中以权益的比例为概率，随机选出slotleader（就是在这个slot中打包区块的节点）。

       以每一个epoch为分析单位，那么只要每一个epoch的执行流程是成立的，那么不断重复epoch生成的链就是成立的。 那么现在就分别解决这两个问题。

一、产生一个随机种子ρ

• 简单随机数协议(Coin-Tossing)

       首先要产生一个随机种子，产生随机种子的方法在密码学中属于交互式协议。

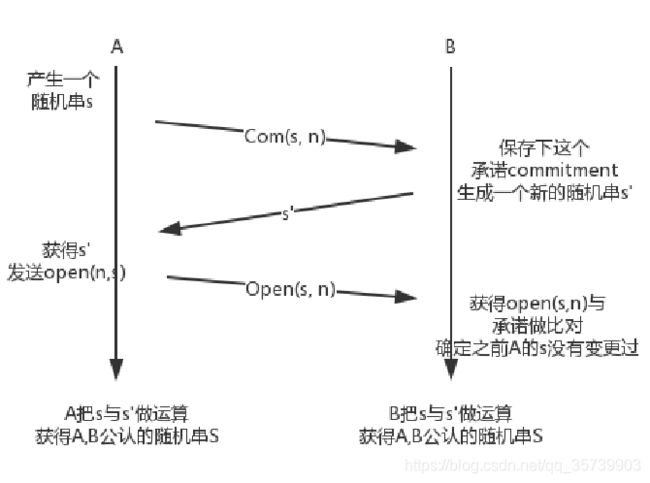
       需要介绍一下简单随机数协议（Coin-Tossing），是为了在多方通信中，通过随机数和双方交互，最终得到一个统一的，被所有人认可的随机数。如图所示：

        A首先产生一个随机串s和一个nonce，然后用A和B都认可的加密方式进行加密。

       此时加密的结果称为一个Commitments（翻译过来是承诺)，A把这个承诺发送给B，此时相当于B知道A已经产生了一个东西，虽然不知内容是什么，但是它已经存在了。

       B保存A的承诺，然后生成一个自己的随机字串s'，并发送给A 。

       此时A同时具有了A自己的字串s和B的字串s'，那么A就发送一个open（翻译过来是揭露，这是未加密的信息)给B，包含自己一开始的s和nonce。

       B收到open后对open的数据加密，把结果和之前的承诺comittment做对比，发现一致，那么B就可以肯定 A发送的open里的数据 就是一开始生成好并存在的。

      这是A对B发送，同理B对A也进行同样的操作，最终A和B都分别拿到了对方的随机串，并且被双方所认可这些信息是没有被篡改过的。

      当把这个两方的交互扩展为多方的时候，就是一个多方的交互式随机数生成协议了。

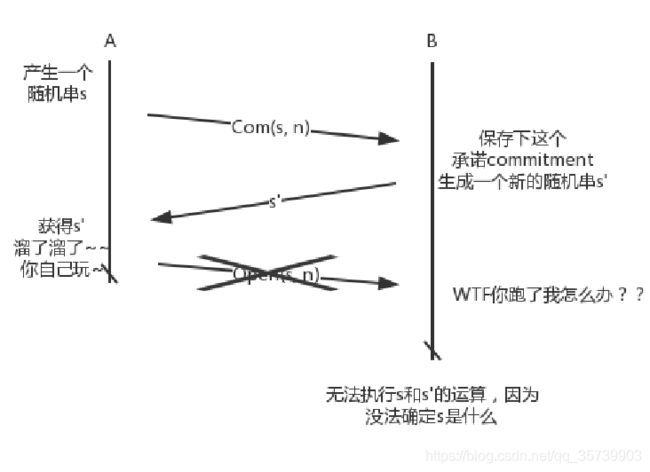
      但是呢，我们可以看到，这种交互至少需要3步，要达成这样的交互式协议是不能比3步更少的。如果少于了3步，协议就会出现问题

       比如

       1.A首先产生一个随机串s和nonce，并发送对应的Commitment给B

       2.B给了A自己的s'，此时A和B完成基本的信息交互

       3.但是此时A没有响应(不管是作恶还是自己掉线)，总之A没有把自己的open发送给了B，此时会导致整个协议无法执行下去，因为现在A具有了所有的信息，但是B没有所有的信息，所以无法达成双方都认可的随机串。

      A这样的行为会可能导致最终的协议无法执行下去，进而被中断(Abort)。特别是多方交互的情况下，太多的通信就会造成整个网络的拥堵。

      所以如果能在尽可能少的通信下(比如三步)，又希望协议不会因为中断而无法运作下去，这样的目的就被称为guarantee output delivery(G.O.D)

• Verifiable Secret Sharing (VSS)

       那么为了保证G.O.D这个目标成立，论文中引入一些新的机制。那就是可验证秘密共享协议VSS 。

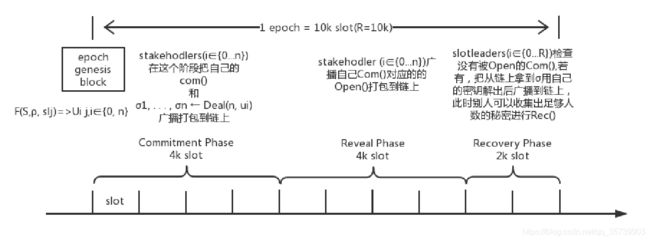
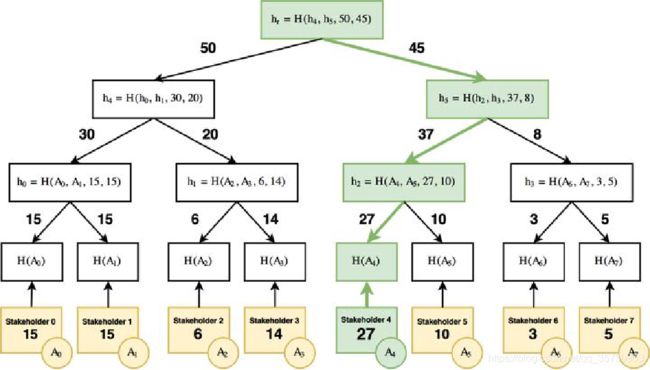
       基本思想： 把一个秘密 S 通过 share(s) 拆分成 m 份，分发给m个人，每个人拿到其中的一片，并不知道整个S 是什么，但是只要收集到另外t (t

       特点： 每个人并不是要拿到所有人的秘密，而是拿到某些人的秘密组合，就可以重新恢复出原来的秘密S。

       这只是从原理上简单描述VSS能够做到的事情。我们可以发现，他特点就在于，。。。 这个特点可以达成一个功能：例如A向大家宣告我有一个信息，然后A就可以用VSS把这个信息拆分并分发给所有人，但是所有人又不知道这个信息整体是什么。此时，即使A掉线或者跑路了，大家也可以互相通信恢复出完整信息。

      显然，VSS就是用来解决简单随机数协议中断执行的问题.

• G.O.D coin tossing

        现在大致捋一下思路： 简单随机数协议的问题在于，要是 A 没有发送open给B，协议就无法执行下去。那么联系起VSS的性质，我们就可以得出：要是open因为某些原因导致协议中断，那事先把open分发给所有人不就可以了么？即使A掉线了，大家也可以互相通信恢复出A一开始给出的承诺是什么，使得简单随机数协议能够正常执行下去，这样得到大家都认可的的随机种子ρ了。

      所以论文把 可验证秘密共享协议 和 简单随机数协议 结合起来的时候，就可以达成 G.O.D 的目标，称为 “G.O.D coin tossing” ,上图是论文对算法的形式化描述。

     那么它的具体流程是这样的，如下图：

      规定

        1.把每个epoch的slot分成10等份（k的倍数，这里令k=1），三个阶段：Commitment Phase, Revel Phase, Recovery Phase，分别占比4:4:2

        2.在每个epoch初始块生成的时候(也就是ρ产生的时候)，实际上每一个slot的slotleader已经被选出来了，也就是说在每个epoch开始的时候，就已经选定每个slot是谁出块了，选出的方式等会详细解释。

       要注意在前两个阶段是所有的stakeholder都参与，然后Recovery阶段只有被选中的stakeholders才参与。

      具体流程如下：

       首先，在Commitment阶段，也就是在整个epoch的前4/10的时间，所有的stakeholders必须生成自己的随机串并处理，然后把这个内容广播出去，被前4k个slot的leader打包进入区块。(当然如果这个时间内没有把自己的随机串广播出去的话，就相当于放弃参与下一个epoch的竞选了)，而这个处理的内容是两个部分：

       · 这个随机字串的承诺Commitment 。

       · 使用这些slotleader的公钥把Open的内容进行加密，然后用可验证秘密共享协议VSS把加密后的内容分发给所有的slotleader。

        然后，在Reveal阶段中，也就是epoch中间的4/10时间，这些stakeholders把自己的Open广播出去。此时就会出现有人跑路，有人掉线，网络不好等情况，就导致这个stakeholder的Open没有被打包到链中，此时若没有下一个阶段救场的话，就相当于简单随机数协议中断了。如果所有的Open都在的话，那当然就可以得出下一个epoch的ρ是什么了。

        最后，在Recovery阶段的时候，也就是epoch最后2/10的时间，这些诚实的slotleaders (i∈{0...R})，就会检查出有哪些committment没有open，就会把自己得到的对应秘密解密，并广播出去，那么每个人都可以收集到足够的共享秘密而恢复出完整的随机串，满足G.O.D的目标。这就可以得出一个统一的真随机种子ρ了。

       至此，如何在一个epoch中生成一个不可控制的随机数ρ就完成了。

二、如何随机选出slotleader

• 随机选出slotleader

          就是根据随机种子ρ，在当前epoch中以权益的比例为概率，选出slotleader是哪个stakeholder，使用的是“follow-the-satoshi”算法。

          Follow-The-Satoshi算法最原始是来自于论文：Proof of Activity: Extending Bitcoin’s Proof of Work via Proof of Stake。

          算法原理：将所有的权益(stakeholder)组成一棵Merkletree，形式是非叶子节点的权重为左右子树的权重之和，叶子节点的权重是某个stakeholder的权益值。然后根据随机数在左右子树中进行选择，最终会按照权益的比例选出对应的stakeholder。

         github上有人对其作了一个模拟实现：https://github.com/Realiserad/fts-tree

        以上图为例，假设前面生成的随机种子是65，每次执行伪随机后可以获得序列{65, 20,15}，这颗树的组成是把stakeholders按默克尔树组织好，附加上每一条边代表两个叶子权益之和。那么我们根据序列从树根开始查找开始：

        随机数是65，左边权益是50，那么65>50所以选择右边。

        执行伪随机得到20，左边权益37，20<37，选择左边。

        执行伪随机得到15，左边权益27，15<27，选择左边，所以最终选择出A4作为这一轮的slotleader。

        那么其他节点如何验证这个slotleader的合法性呢？因为是使用一个真随机数作为种子，那么只要所有人拿到的真随机数种子是一致的，那么根据这个规则选出的slotleader就是一致的。

        所以就是可以解释G.O.D coin tossing算法中的问题，只要能够得到每个epoch初始块中的随机种子ρ和权益集合S，那么就相当于得到当前这个epoch中所有的slotleader都是谁了。

• 总结

       所以解决了这两个问题，就可以随机的选出记账者，改进了pos的安全性。

       论文实际上写的很复杂并且篇幅很长有近60页··· 我是主要参考Omni-Space关于这个共识算法的文章，以及论文和作者在会议上的演讲视频以及相关学习资料，汇总了这个共识机制整体的执行流程和中间的一些细节，可能部分内容和图片上有所重复，仅供参考。        

       最后，引用Omni-Space在文章“Cardano（ADA）的共识算法Ouroboros”中的一句话吧：“总的来说，Ouroboros开启了pos的新篇章，最重要的不只是给出这样一种pos的思路，更多的是提出对pos的一个论证方式，这种论证的方式可以延续到其他共识算法的证明中。”