论文阅读《Revisiting Stereo Depth Estimation From a Sequence-to-Sequence Perspective with Transformers》
论文地址:https://ieeexplore.ieee.org/document/9711118
源码地址:https://github.com/mli0603/stereo-transformer
概述
此文提出了一个基于transformer的匹配方法名为Stereo Transformer (STTR),该方法使用位置信息与注意力机制来提高模型表现。该模型有以下几点优势:
- 放宽了视差范围限制
- 明确了遮挡区域并进行了置信度估计
- 保证了匹配的唯一性
该模型的创新点如下:
- 基于transformer架构,使用可以选择的自注意力与交叉注意力机制和最优传输理论来进行特征匹配
- 提出一个相对位置编码来增强匹配特征的表达性
- 使用注意力机制来处理匹配过程中的易混淆特征
- 提出一种内存节省的STTR模型,使得模型能在现有的硬件上训练与推理
模型架构
特征提取层
使用了权值共享的编解码结构来提取左右视图的特征,在编码器上使用残差结构与池化金字塔结构来得提取更多的全局语义信息。在解码器部分使用转置卷积与密集连接块。每个像素的特征为 e I e_I eI,维度为 C e C_e Ce,输出的特征图与输入图像尺寸保持一致。
Transformer
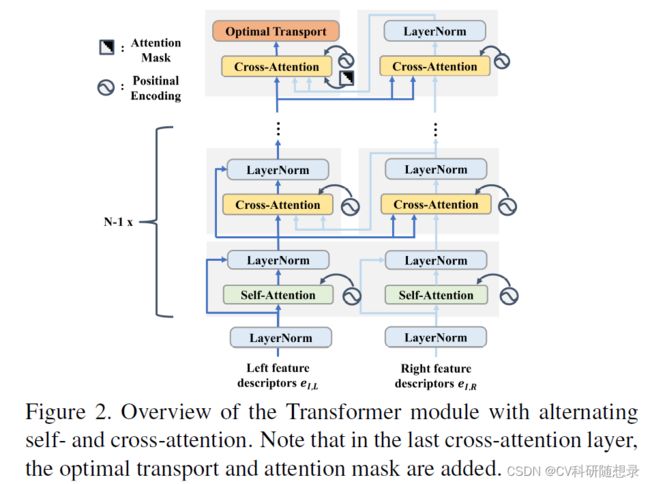
在文中,使用自注意力来计算同幅图形对应行的像素点之间的注意力,使用交叉注意力来计算不同左右图像之间对应行上像素的注意力,如图2所示:
注意力
注意力模块使用向量内积计算key与query的相似性作为注意力,然后使用注意力来对value加权,文中使用多头注意力来计算提升匹配特征的表达性,即:将匹配特征 C e C_e Ce 分为 N h N_h Nh 组得: C h = C e / N h C_h=C_e/N_h Ch=Ce/Nh ,其中 C h C_h Ch 是每组特征的维度。对于每个head组: Q h = W Q h e I + b Q h K h = W K h e I + b K h V h = W V h e I + b V h , (1) \begin{array}{l} \mathcal{Q}_{h}=W_{\mathcal{Q}_{h}} e_{I}+b_{\mathcal{Q}_{h}} \\ \mathcal{K}_{h}=W_{\mathcal{K}_{h} e_{I}}+b_{\mathcal{K}_{h}} \\ \mathcal{V}_{h}=W_{\mathcal{V}_{h}} e_{I}+b_{\mathcal{V}_{h}}, \end{array}\tag{1} Qh=WQheI+bQhKh=WKheI+bKhVh=WVheI+bVh,(1)
其中, W Q h , W K h , W V h ∈ R C h × C h , b Q h , b K h , b V h ∈ R C h W_{\mathcal{Q}_{h}}, W_{\mathcal{K}_{h}}, W_{\mathcal{V}_{h}} \in \mathbb{R}^{C_{h} \times C_{h}}, b_{\mathcal{Q}_{h}}, b_{\mathcal{K}_{h}}, b_{\mathcal{V}_{h}} \in \mathbb{R}^{C_{h}} WQh,WKh,WVh∈RCh×Ch,bQh,bKh,bVh∈RCh,此外,有: α h = softmax ( Q h T K h C h ) (2) \alpha_{h}=\operatorname{softmax}\left(\frac{\mathcal{Q}_{h}^{T} \mathcal{K}_{h}}{\sqrt{C_{h}}}\right) \tag{2} αh=softmax(ChQhTKh)(2)
输出特征表示为:
V O = W O Concat ( α 1 V 1 , … , α N h V N h ) + b O (3) \mathcal{V}_{\mathcal{O}}=W_{\mathcal{O}} \text { Concat }\left(\alpha_{1} \mathcal{V}_{1}, \ldots, \alpha_{N_{h}} \mathcal{V}_{N_{h}}\right)+b_{\mathcal{O}}\tag{3} VO=WO Concat (α1V1,…,αNhVNh)+bO(3)
其中 W O ∈ R C e × C e W_{\mathcal{O}} \in \mathbb{R}^{C_{e} \times C_{e}} WO∈RCe×Ce且 b O ∈ R C e b_{\mathcal{O}} \in \mathbb{R}^{C_{e}} bO∈RCe。基于残差学习的思想,输出特征表示为:
e I = e I + V O (4) e_{I}=e_{I}+\mathcal{V}_{\mathcal{O}}\tag{4} eI=eI+VO(4)
在自注意力中, Q h , K h , V h \mathcal{Q}_{h}, \mathcal{K}_{h}, \mathcal{V}_{h} Qh,Kh,Vh从同一张图片中计算而来,而在交叉注意力中, Q h \mathcal{Q}_{h} Qh从源图像中计算而来,而 K h , V h \mathcal{K}_{h}, \mathcal{V}_{h} Kh,Vh 从目标图像中获得,交叉注意力是源图像与目标图像之间双向交叉计算的过程。
相对位置编码
在无纹理的大区域间,匹配像素之间的匹配性可能是模糊的,这种模糊性可以通过考虑与突出特征(如边缘)有关的相对位置信息来解决,为此,文中通过相对位置编码而非绝对位置编码来为匹配特征提供空间信息:
e = e I + e p (5) e = e_I + e_p\tag{5} e=eI+ep(5)
其中式 2 中第 i i i 与 j j j 个像素之间的注意力可以表示为(忽略bias项):
α i , j = e I , i T W Q T W K e I , j ⏟ (1) data-data + e I , i T W Q T W K e p , j ⏟ (2) data-position + e p , i T W Q T W K e I , j ⏟ (3) position-data + e p , i T W Q T W K e p , j ⏟ (4) position-position . (6) \begin{aligned} \alpha_{i, j}=\underbrace{e_{I, i}^{T} W_{\mathcal{Q}}^{T} W_{\mathcal{K}} e_{I, j}}_{\text {(1) data-data }}+\underbrace{e_{I, i}^{T} W_{\mathcal{Q}}^{T} W_{K} e_{p, j}}_{\text {(2) data-position }}+ \underbrace{e_{p, i}^{T} W_{\mathcal{Q}}^{T} W_{\mathcal{K}} e_{I, j}}_{\text {(3) position-data }}+\underbrace{e_{p, i}^{T} W_{\mathcal{Q}}^{T} W_{\mathcal{K}} e_{p, j}}_{\text {(4) position-position }} . \end{aligned}\tag{6} αi,j=(1) data-data eI,iTWQTWKeI,j+(2) data-position eI,iTWQTWKep,j+(3) position-data ep,iTWQTWKeI,j+(4) position-position ep,iTWQTWKep,j.(6)
其中第4项只依赖于位置信息,而视差估计不应该含有只依赖于位置编码的项,故将式6修正如下:
α i , j = e I , i T W Q T W K e I , j ⏟ (1) data-data + e I , i T W Q T W K e p , i − j ⏟ (2) data-position + e p , i − j T W Q T W K e I , j ⏟ (3) position-data , (7) \begin{aligned} \alpha_{i, j}=\underbrace{e_{I, i}^{T} W_{\mathcal{Q}}^{T} W_{\mathcal{K}} e_{I, j}}_{\text {(1) data-data }}+ \underbrace{e_{I, i}^{T} W_{\mathcal{Q}}^{T} W_{K} e_{p, i-j}}_{\text {(2) data-position }}+\underbrace{e_{p, i-j}^{T} W_{\mathcal{Q}}^{T} W_{\mathcal{K}} e_{I, j}}_{\text {(3) position-data }}, \end{aligned}\tag{7} αi,j=(1) data-data eI,iTWQTWKeI,j+(2) data-position eI,iTWQTWKep,i−j+(3) position-data ep,i−jTWQTWKeI,j,(7)
其中, e p , i − j e_{p, i-j} ep,i−j为第 i i i与 j j j 之间的位置编码。注: e p , i − j ≠ e p , j − i e_{p, i-j} \neq e_{p, j-i} ep,i−j=ep,j−i。注意力是由匹配像素之间的相似度和位置编码共同计算而来。
最优传输
熵-规则化最优传输由于其软分配和可微调性,被证明有利于稀疏特征和语义对应匹配的相关任务。给定边缘分布 a a a 与 b b b 的代价矩阵 M M M , 熵-规则化最优传输旨在求取最优联接矩阵:
T = argmin T ∈ R + I w × I w ∑ i , j = 1 I w , I w T i j M i j − γ E ( T ) s.t. T 1 I w = a , T T 1 I w = b (8) \begin{array}{l} \mathcal{T}=\underset{\mathcal{T} \in R_{+}^{I_w\times I_{w}}}{\operatorname{argmin}} \sum_{i, j=1}^{I_{w}, I_{w}} \mathcal{T}_{i j} M_{i j}-\gamma E(\mathcal{T}) \\ \text { s.t. } \mathcal{T} 1_{I_{w}}=a, \mathcal{T}^{T} 1_{I_{w}}=b \end{array}\tag{8} T=T∈R+Iw×Iwargmin∑i,j=1Iw,IwTijMij−γE(T) s.t. T1Iw=a,TT1Iw=b(8)
其中 E ( T ) E(\mathcal{T}) E(T) 为熵正则化项。若两个边缘分布 a , b a,b a,b 是均匀分布, T \mathcal{T} T 对于分配问题而言也是最优的,其通过增加一个软约束来降低模糊性。此时可以通过迭代的 Sinkhorn 算法来求取公式 8 的最优解。同时, T \mathcal{T} T 的每个元素代表匹配对之间的匹配概率,这种问题与式2中的softmax attention是相似的。
实际上,由于遮挡导致部分像素不存在对应匹配的像素,为此,文中使用一个带有学习参数的 ϕ \phi ϕ 的dustbins机制来表示这些不存在匹配点的像素的代价值。
注意力掩码
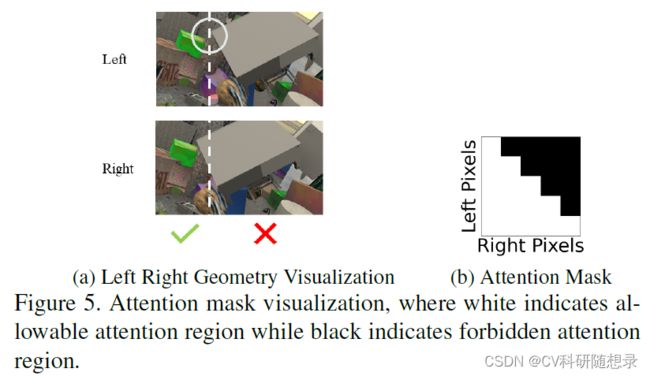
&ems;不妨用 x L , x R x_L,x_R xL,xR 分别来表示左右图像之间的同名点的位置,在极线校正后的图像对中,总有 x R < x L x_R
初始视差与遮挡回归
文中使用分配矩阵 T \mathcal{T} T 中的最大概率视差值 k k k 来表示初始预测视差,在最大视差邻域建立 3 p x 3px 3px 的窗口,再将窗口内的视差值进行归一化后作为权重进行加权:
t ~ l = t l ∑ l ∈ N 3 ( k ) t l , for l ∈ N 3 ( k ) (9) \tilde{t}_{l}=\frac{t_{l}}{\sum_{l \in \mathcal{N}_{3}(k)} t_{l}}, \text { for } l \in \mathcal{N}_{3}(k)\tag{9} t~l=∑l∈N3(k)tltl, for l∈N3(k)(9)
d ~ raw ( k ) = ∑ l ∈ N 3 ( k ) d l t ~ l (10) \tilde{d}_{\text {raw }}(k)=\sum_{l \in \mathcal{N}_{3}(k)} d_{l} \tilde{t}_{l}\tag{10} d~raw (k)=l∈N3(k)∑dlt~l(10)
为此,对于遮挡概率 p o c c ( k ) p_{occ}(k) pocc(k) 表示为:
p o c c ( k ) = 1 − ∑ l ∈ N 3 ( k ) t l (11) p_{o c c}(k)=1-\sum_{l \in \mathcal{N}_{3}(k)} t_{l}\tag{11} pocc(k)=1−l∈N3(k)∑tl(11)
内容自适应层
初始视差图计算过程中没有考虑多行之间的内容信息,为此,文中使用一份基于卷积的自适应层来考虑多行之间的内容信息。如图3所示:

将初始视差图与遮挡图沿着通道维度进行拼接,继而使用两个卷积block与ReLu激活单元来聚合遮挡信息。最终使用Sigmoid激活层来计算遮挡图,同时使用残差Block来对最终的视差图进行预测。
损失函数
使用Relative Response loss L r r L_{rr} Lrr 来表示匹配损失,模型的目标是通过最大化目标目标视差的注意力,同时使用线性插值来计算匹配概率 t ⋆ t^\star t⋆。因此,对于标签视差值为 d g t , i d_{gt,i} dgt,i 的左视图第 i i i 像素有:
t i ∗ = interp ( T i , p i − d g t , i ) L r r = 1 N M ∑ i ∈ M − log ( t i ∗ ) + 1 N U ∑ i ∈ U − log ( t i , ϕ ) (12) \begin{aligned} t_{i}^{*} & =\operatorname{interp}\left(\mathcal{T}_{i}, p_{i}-d_{g t, i}\right) \\ L_{r r} & =\frac{1}{N_{\mathcal{M}}} \sum_{i \in \mathcal{M}}-\log \left(t_{i}^{*}\right)+\frac{1}{N_{\mathcal{U}}} \sum_{i \in \mathcal{U}}-\log \left(t_{i, \phi}\right) \end{aligned}\tag{12} ti∗Lrr=interp(Ti,pi−dgt,i)=NM1i∈M∑−log(ti∗)+NU1i∈U∑−log(ti,ϕ)(12)
其中, i n t e r p interp interp 代表线性插值,而 t i , ϕ t_{i, \phi} ti,ϕ 代表不匹配概率。最后对初始视差图 L d 1 , r L_{d1, r} Ld1,r 与最终视差图 L d 1 , f L_{d1, f} Ld1,f 与GT进行算 L 1 L_1 L1 平滑损失。最后的遮挡图使用二进制熵损失来进行监督约束,最终损失函数如式14所示:
L = w 1 L r r + w 2 L d 1 , r + w 3 L d 1 , f + w 4 L b e , f , (14) L=w_{1} L_{r r}+w_{2} L_{d 1, r}+w_{3} L_{d 1, f}+w_{4} L_{b e, f},\tag{14} L=w1Lrr+w2Ld1,r+w3Ld1,f+w4Lbe,f,(14)
低显存模型优化:
模型在float 32的计算精度下的显存消耗为:memory consumption = 32 I h I w 2 N h N = 32I_hI^2_wN_hN =32IhIw2NhN,若给定图像尺寸 I w = 960 , I h = 540 , N h = 8 I_w=960, I_h=540, N_h=8 Iw=960,Ih=540,Nh=8,且在训练阶段的 N = 6 N=6 N=6 层时候的显存消耗为216G。
使用梯度checkpointing对每个自注意力与交叉注意力层进行处理,在前向推理的过程不保存中间变量,而在反向传播的过程在此进行前向传播,重新计算梯度值。为此,内存消耗仅受单个注意力层的限制,使得网络可以在注意力层数维度 N N N 上无限扩展。进一步使用混合精度训练与使用注意跨度 s > 1 s>1 s>1 来对特征描述符进行稀疏采样(降采样)来降低显存消耗。
实验结果分析
文中在Scene Flow上进行了对注意力掩码层、最优传输层、内容自适应层、和位置编码机制都进行了消融实验,实验结果如表1所示: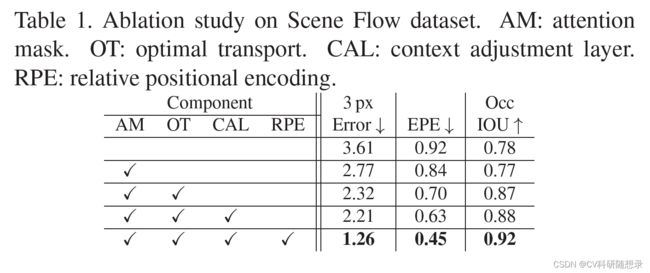
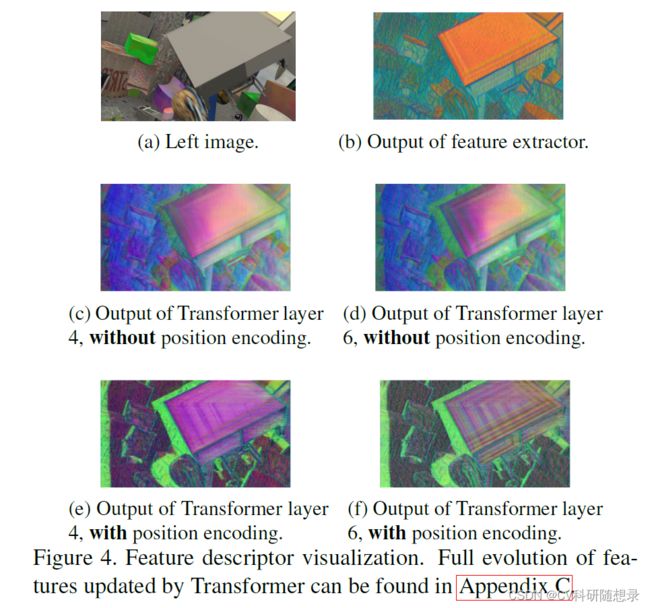
相对位置编码:为了将相对位置编码的作用可视化,文中基于PCA来对匹配特征进行降维到维度为3。对于无纹理区域(如图4(a)所示),其特征如图4(b)所示,具有相似的模式。在没有位置编码时,随着层数的加深,深度图只是在整个过程中发生变化,如图4(c-d)所示。若增加了位置编码,如图4(e)所示,在第4层出现了与边缘平行的条纹,最终条纹传播到第6层的整个区域,如图4(f)所示,说明相对位置编码可以解决无纹理区域的混淆问题。
注意力的泛化:原则上,STTR允许预测视差范围随着图像宽度的变化而变化尽管如此,以下测试STTR是否可以预测比训练阶段更广的视差范围的场景。在实验中,只是用视差范围为1-192的数据来训练模型,而在测试阶段,模型能在1px的误差范围内做出的最大差距预测是458px,这证明了模型泛化能力优秀。
注意力跨度:文中同时分析了自注意力与交叉注意力的注意力跨度(所有像素上的注意值分布)。实验结果如附录D所示,自注意力与交叉注意力都从相对的全局信息开始(300px),然后转移到局部信息(114px是自注意力,15px是交叉注意力)。全局信息主要用于浅层,对后期层的视差细化没有实质性的贡献。这表明未来的工作有机会根据前几层的注意力跨度逐渐减少搜索窗口以提高效率。

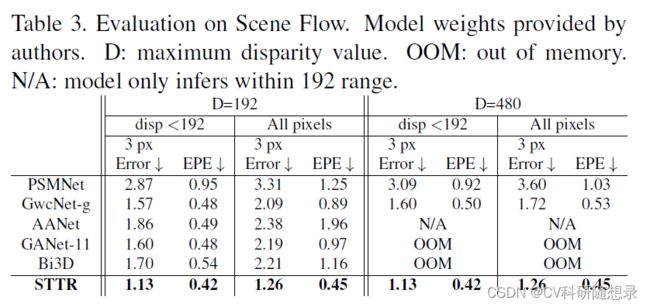
SceneFlow数据集实验结果:表3为Scene Flow的预训练结果,当只对视差小于192的像素进行评估时,STTR的表现与之前的工作相当(第2-3列)。然而,STTR在无视差范围限制时,而其他方法的最大预测视差 D = 192 D=192 D=192,STTR的表现优于其他方法。为了公平地进行比较,文中使用用 D = 480 D = 480 D=480(涵盖了测试数据集中的所有视差值)对其他方法进行评估。STTR的性能仍然与 D = 192 D = 192 D=192 的设置相同,与其他方法相当。此外,如下图所示,STTR可以准确地识别遮挡区域,这也是比其他方法更优秀的。

跨域泛化:
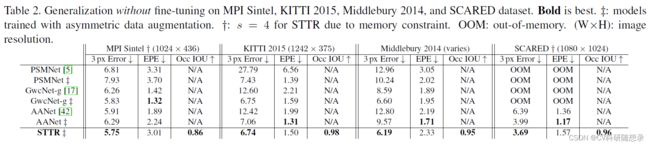
文中将STTR与表2中中的方法进行比较,以考察STTR的跨域泛化能力。作者将其他方法的最大的视差设置为 D = 192 D=192 D=192,并且只评估这个范围内的像素。此外,还用用于STTR的非对称增强技术来训练其余方法,以避免不一致,同时保持原有的训练方案(优化器、学习率、损失和pochs的数量)。STTR的泛化能力在四个数据集中保持了较高的闭塞性IOU,具有可比性。STTR在3 px误差方面表现良好,但在EPE方面却不一定。这是因为如果一个像素被错误地识别为闭塞,就会预测为零的差距,从而导致EPE很大。
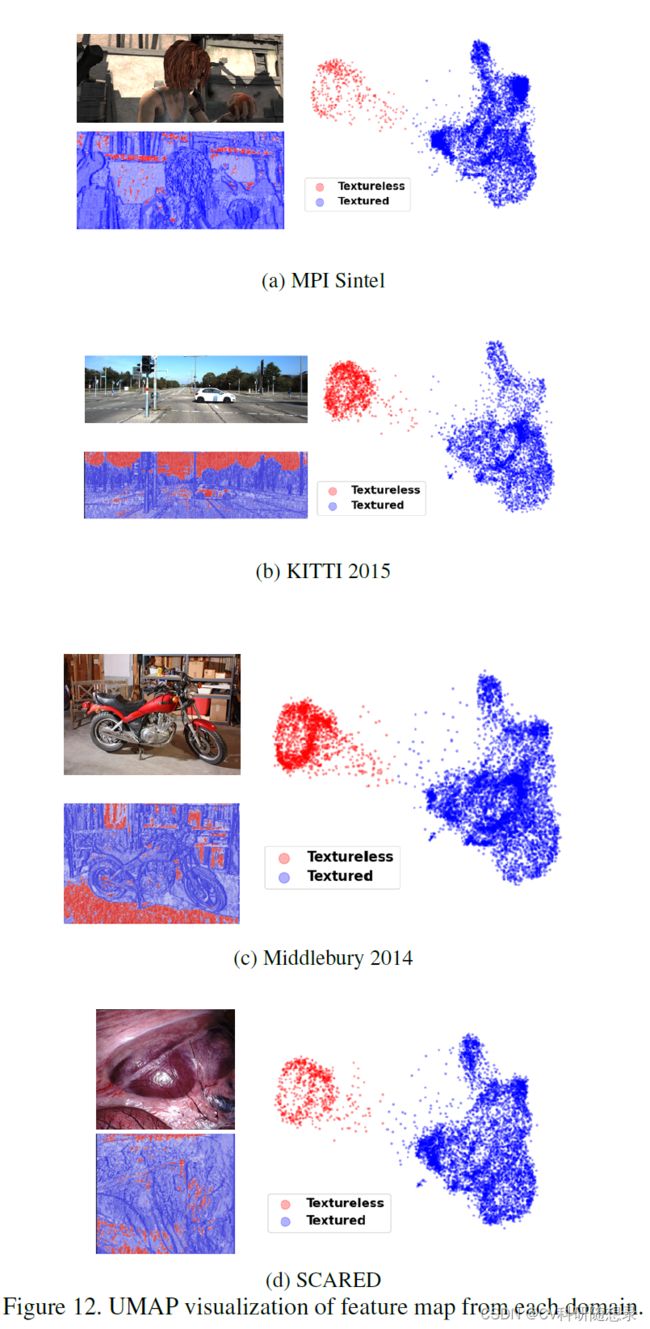
作者在图11中使用UMAP方法对输入的特征图进行了可视化,每个数据点都代表了的一个像素点,从实验结果中可以观察到,由STTR学习的表征特征聚集在两个区域(图11(a)),如果在其余数据集上的一个像素更接近集群的中心点,那么该像素在颜色掩码中的强度就更高。此外,特征提取器将像素分为有纹理(蓝色)和无纹理(红色)区域。颜色掩膜中强度较高的像素大多与纹理边缘相关。为了验证蓝色区域确实比红色区域包含更多的纹理,作者计算了每个数据集的归一化图像强度上的平均 Sobel 边缘梯度。如表5所示,除了SCARED之外,所有数据集在蓝色集群中的边缘梯度都比红色集群大,证实了蓝色集群比红色集群包含更多的 “纹理”。从图12(a-d)中显示了从MPI Sintel、KITTI 2015、Middlebury 2014和SCARED数据集上提取的特征的单独UMAP还原。这种隐性学习的特征聚类提高了STTR的泛化能力,使Transformer匹配过程更加容易。

总结
本文出了一个名为STereo TRsformer的端到端网络架构,它协同了CNN和Transformer架构的优势,命名为STereo TRansformer。从序列到序列匹配的角度重新审视立体深度估计。这种方法有以下的优势:
1)避免了预先指定一个固定的差异范围
2)明确地处理遮挡问题
3)施加一个匹配的唯一性约束。