matlab如何就导数,Matlab微分和导数

Matlab 的 Matlab微分和导数

MATLAB提供用于计算符号导数的diff命令。 以最简单的形式，将要微分的功能传递给diff命令作为参数。

例如，计算函数的导数的方程式 -

例子

创建脚本文件并在其中键入以下代码 -

syms t

f = 3*t^2 + 2*t^(-2);

diff(f)

执行上面示例代码，得到以下结果 -

Trial>> syms t

f = 3*t^2 + 2*t^(-2);

diff(f)

ans =

6*t - 4/t^3

以下是使用Octave 计算的写法 -

pkg load symbolic

symbols

t = sym("t");

f = 3*t^2 + 2*t^(-2);

differentiate(f,t)

执行上面示例代码，得到以下结果 -

ans =

6*t - 4/t^3

基本微分规则的验证

下面简要说明微分规则的各种方程或规则，并验证这些规则。 为此，我们将写一个第一阶导数f'(x)和二阶导数f“(x)。

以下是微分的规则 -

规则 - 1

对于任何函数f和g，任何实数a和b是函数的导数：

h(x) = af(x) + bg(x)相对于x，由h’(x) = af’(x) + bg’(x)给出。

规则 - 2

sum和subtraction规则表述为：如果f和g是两个函数，则f'和g'分别是它们的导数，如下 -

(f + g)' = f' + g'

(f - g)' = f' - g'

规则 - 3

product规则表述为：如果f和g是两个函数，则f'和g'分别是它们的导数，如下 -

(f.g)' = f'.g + g'.f

规则 - 4

quotient规则表明，如果f和g是两个函数，则f'和g'分别是它们的导数，那么 -

规则 - 5

多项式或基本次幂规则表述为：如果y = f(x)= x^n，则 -

这个规则的直接结果是任何常数的导数为零，即如果y = k，那么为任何常数 -

f' = 0

规则 - 5

chain规则表述为 - 相对于x的函数h(x)= f(g(x))的函数的导数是 -

h'(x)= f'(g(x)).g'(x)

例子

创建脚本文件并在其中键入以下代码 -

syms x

syms t

f = (x + 2)*(x^2 + 3)

der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)

der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)

der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)

der4 = diff(f)

f = (x^2 + 1)^17

der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)

der6 = diff(f)

执行上面示例代码，得到 以下结果 -

f =

(x^2 + 3)*(x + 2)

der1 =

2*x*(x + 2) + x^2 + 3

f =

(t^(1/2) + t^3)*(t^2 + 3)

der2 =

(t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)

f =

(x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)

der3 =

(2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)

f =

(2*x^2 + 3*x)/(x^3 + 1)

der4 =

(4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2

f =

(x^2 + 1)^17

der5 =

34*x*(x^2 + 1)^16

f =

1/(t^3 + 3*t^2 + 5*t - 9)^6

der6 =

-(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

以下是对上面示例的Octave写法 -

pkg load symbolic

symbols

x=sym("x");

t=sym("t");

f = (x + 2)*(x^2 + 3)

der1 = differentiate(f,x)

f = (t^2 + 3)*(t^(1/2) + t^3)

der2 = differentiate(f,t)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)

der3 = differentiate(f,x)

f = (2*x^2 + 3*x)/(x^3 + 1)

der4 = differentiate(f,x)

f = (x^2 + 1)^17

der5 = differentiate(f,x)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)

der6 = differentiate(f,t)

指数，对数和三角函数的导数

下表提供了常用指数，对数和三角函数的导数，

例子

创建脚本文件并在其中键入以下代码 -

syms x

y = exp(x)

diff(y)

y = x^9

diff(y)

y = sin(x)

diff(y)

y = tan(x)

diff(y)

y = cos(x)

diff(y)

y = log(x)

diff(y)

y = log10(x)

diff(y)

y = sin(x)^2

diff(y)

y = cos(3*x^2 + 2*x + 1)

diff(y)

y = exp(x)/sin(x)

diff(y)

执行上面示例代码，得到以下结果 -

y =

exp(x)

ans =

exp(x)

y =

x^9

ans =

9*x^8

y =

sin(x)

ans =

cos(x)

y =

tan(x)

ans =

tan(x)^2 + 1

y =

cos(x)

ans =

-sin(x)

y =

log(x)

ans =

1/x

y =

log(x)/log(10)

ans =

1/(x*log(10))

y =

sin(x)^2

ans =

2*cos(x)*sin(x)

y =

cos(3*x^2 + 2*x + 1)

ans =

-sin(3*x^2 + 2*x + 1)*(6*x + 2)

y =

exp(x)/sin(x)

ans =

exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

以下代码是上面代码的Octave写法 -

pkg load symbolic

symbols

x = sym("x");

y = Exp(x)

differentiate(y,x)

y = x^9

differentiate(y,x)

y = Sin(x)

differentiate(y,x)

y = Tan(x)

differentiate(y,x)

y = Cos(x)

differentiate(y,x)

y = Log(x)

differentiate(y,x)

% symbolic packages does not have this support

%y = Log10(x)

%differentiate(y,x)

y = Sin(x)^2

differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)

differentiate(y,x)

y = Exp(x)/Sin(x)

differentiate(y,x)

计算高阶导数

要计算函数f的较高导数，可使用diff(f，n)。

计算函数的二阶导数公式为 -

f = x*exp(-3*x);

diff(f, 2)

MATLAB执行上面代码将返回以下结果 -

ans =

9*x*exp(-3*x) - 6*exp(-3*x)

以下是使用Octave重写上面示例，代码如下 -

pkg load symbolic

symbols

x = sym("x");

f = x*Exp(-3*x);

differentiate(f, x, 2)

例子

在这个例子中，要解决一个问题。由给定函数y = f(x)= 3sin(x)+ 7cos(5x)，来找出方程f“+ f = -5cos(2x)是否成立。

创建脚本文件并在其中键入以下代码 -

syms x

y = 3*sin(x)+7*cos(5*x); % defining the function

lhs = diff(y,2)+y; %evaluting the lhs of the equation

rhs = -5*cos(2*x); %rhs of the equation

if(isequal(lhs,rhs))

disp('Yes, the equation holds true');

else

disp('No, the equation does not hold true');

end

disp('Value of LHS is: '), disp(lhs);

运行文件时，会显示以下结果 -

No, the equation does not hold true

Value of LHS is:

-168*cos(5*x)

以上是上面示例的Octave写法 -

pkg load symbolic

symbols

x = sym("x");

y = 3*Sin(x)+7*Cos(5*x); % defining the function

lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation

rhs = -5*Cos(2*x); %rhs of the equation

if(lhs == rhs)

disp('Yes, the equation holds true');

else

disp('No, the equation does not hold true');

end

disp('Value of LHS is: '), disp(lhs);

查找曲线的最大和最小值

如果正在搜索图形的局部最大值和最小值，基本上是在特定地点的函数图上或符号变量的特定值范围内查找最高点或最低点。

对于函数y = f(x)，图形具有零斜率的图上的点称为固定点。 换句话说，固定点是f'(x)= 0。

要找到微分的函数的固定点，需要将导数设置为零并求解方程。

示例

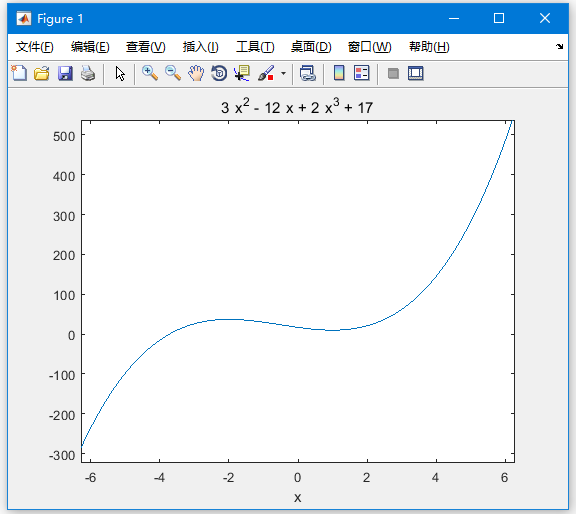
要找到函数f(x)= 2x3 + 3x2 - 12x + 17的固定点

可参考以下步骤 -

首先输入函数并绘制图，代码如下 -

syms x

y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function

ezplot(y)

执行上面示例代码，得到以下结果 -

以上是上面示例的Octave写法 -

pkg load symbolic

symbols

x = sym('x');

y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)

print -deps graph.eps

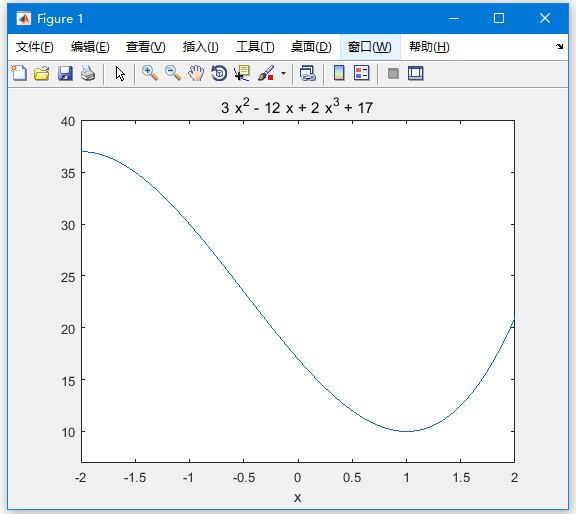
我们的目标是在图上找到一些局部最大值和最小值，假设要找到图中间隔在[-2,2]的局部最大值和最小值。参考以下示例代码 -

syms x

y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function

ezplot(y, [-2, 2])

执行上面示例代码，得到以下结果 -

以下是上面示例的Octave写法 -

pkg load symbolic

symbols

x = sym('x');

y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])

print -deps graph.eps

接下来，需要计算导数。

g = diff(y)

MATLAB执行代码并返回以下结果 -

g =

6*x^2 + 6*x - 12

以下是上面示例的Octave写法 -

pkg load symbolic

symbols

x = sym("x");

y = 2*x^3 + 3*x^2 - 12*x + 17;

g = differentiate(y,x)

接下来求解导数函数g，得到它变为零的值。

s = solve(g)

MATLAB执行代码并返回以下结果 -

s =

1

-2

以下是上面示例的Octave写法 -

pkg load symbolic

symbols

x = sym("x");

y = 2*x^3 + 3*x^2 - 12*x + 17;

g = differentiate(y,x)

roots([6, 6, -12])

这与我们设想情节一致。 因此，要评估临界点x = 1，-2处的函数f。可以使用subs命令替换符号函数中的值。

subs(y, 1), subs(y, -2)

MATLAB执行代码并返回以下结果 -

ans =

10

ans =

37

以下是上面示例的Octave写法 -

pkg load symbolic

symbols

x = sym("x");

y = 2*x^3 + 3*x^2 - 12*x + 17;

g = differentiate(y,x)

roots([6, 6, -12])

subs(y, x, 1), subs(y, x, -2)

因此，在间隔[-2,2]中函数f(x)= 2x^3 + 3x^2 - 12x + 17的最小值和最大值分别为10和37。

求解微分方程

MATLAB提供了用于求解微分方程的dsolve命令。

找到单个方程的解的最基本的dsolve命令形式是 -

dsolve('eqn')

其中eqn是用于输入方程式的文本串。

它返回一个符号解，其中包含一组任意常量，MATLAB标记C1，C2等等。

还可以为问题指定初始和边界条件，以逗号分隔的列表遵循以下公式：

dsolve('eqn','cond1', 'cond2',…)

为了使用dsolve命令，导数用D表示。例如，像f'(t)= -2 * f + cost(t)这样的等式输入为 -

'Df = -2*f + cos(t)'

较高阶导数由D导数的顺序表示。

例如，方程f"(x) + 2f'(x) = 5sin3x应输入为 -

'D2y + 2Dy = 5*sin(3*x)'

下面来看一个一阶微分方程的简单例子：y'= 5y。

s = dsolve('Dy = 5*y')

MATLAB执行代码并返回以下结果 -

s =

C2*exp(5*t)

再来一个二阶微分方程的例子：y“-y = 0，y(0)= -1，y'(0)= 2。

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLAB执行代码并返回以下结果 -

ans =

exp(t)/2 - (3*exp(-t))/2