深入剖析 std::unordered_map 的实现原理之 Hash冲突、退化
本次来讲解下c++中 std::unordered_map的设计原理。
std::unordered_map里面has-a哈希表,它提供的的各个方法基本都是由hashtable封装实现,因此在下文使用hashtable来描述std::unordered_map。
// gnu 实现
template<typename _Key,
typename _Tp,
typename _Hash = hash<_Key>,
typename _Pred = equal_to<_Key>,
typename _Alloc = allocator<std::pair<const _Key, _Tp>>>
class unordered_map
{
typedef __umap_hashtable<_Key, _Tp, _Hash, _Pred, _Alloc> _Hashtable;
_Hashtable _M_h; // 内部的唯一成员变量: hashtable
//...
}
O(1)
数组,可以通过索引index在O(1)的时间复杂度内获取元素,但如果不知道index则要O(N)的时间复杂度来查找该节点。hashtable为了弥补这一缺点,采用一个hash函数来计算元素的索引值,来满足O(1)的搜索时间复杂度。其过程如下。
- 计算元素的哈希值。对于单个键值对
{key, value},计算key对应的哈希值hashcode = hash_func(key)。 - 计算元素在数组中的索引值。由于hashcode不一定处于
[0, bucket_count]范围内,因此需要将hashcode映射到该范围:index = hashcode % bucket_count。
上面两步以O(1)时间复杂度获取了元素在数组中的索引值index,进一步,则能以O(1)时间复杂度给该索引位置赋值或者获取该索引位置的值。两个步骤可实现如下:
size_t bucket_index(const std::unordered_map<int, int>& map, int key) {
size_t bucket_count = map.bucket_count(); // map 的桶的个数
const auto& hash_func = map.hash_function(); // hash函数
size_t hash_code = hash_func(key); // 计算hashcode
// 键key将插入的桶位置
return hash_code % bucket_count;
}
bucket_index函数时间复杂度是O(1)。在C++中,std::unordered_map提供的bucket(key)方法实现了相同的功能,即计算键key在数组中位置,下面可以验证下bucket_index(...) 的正确性。
int main(int argc, char const *argv[]) {
std::unordered_map<int, int> map(5); // 桶的大小为5
int key = 8;
// 如果 bucket_index(map, key) != map.bucket(key),
// 会触发 abort 中断
assert( bucket_index(map, key) == map.bucket(key));
// 计算结果
std::cout<<"index: "<< bucket_index(map, key) << std::endl;
}
// 输出
$ g++ main.cc -o main && ./main
index: 3
上面两个步骤,是插入、搜索一个节点的过程,能够以O(1)的时间复杂度。但若同时存在几个节点的hashcode值一样,那么后面插入的节点岂不是会覆盖前面的值?这个问题即 hash冲突。
hash冲突
在正式讲解hash冲突之前,先介绍一个术语:在hashtable中,数组的每一个元素叫做桶(bucket)。
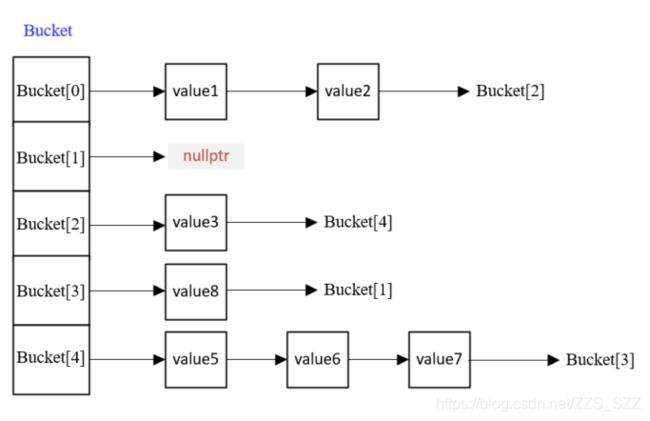
为了解决hash冲突,hashtable在每个桶里bucket[index]不再直接存储待插入节点的值,而是存储一个哨兵节点,使其指向一个链表,由这个链表来存储每次插入节点的值:
- 桶的索引值index依然是
bucket_index函数的计算方式,即通过待插入节点的键来获取 - 待插入节点的值在哨兵指向的链表头部插入,由于是头部插入整个插入过程还是O(1)时间复杂度。
当发生hash冲突时,将所有hashcode相同的节点都插入到同一个链表中,如下图所示。由于采用的是头部插入法,那么即便是发生了hash冲突,此时插入时间复杂度也依然是O(1)。
上述解决hash冲突的方法,叫做开链法。此时,hash冲突的问题似乎解决了,能够插入多个hashcode一样的节点,并且插入操作的时间复杂度仍然是O(1)。
但是!!!,当出现严重的hash冲突,会造成bucket[idx]指向的链表节点很长,此时搜索和删除一个节点的时间复杂度最坏却可能变成O(N),即哈希表已经退化成链表,那么就违背了一开始设计hashtable的初衷,即弥补数组O(N)的搜索、删除时间复杂度。
hash退化
负载因子
为了解决hash退化,引入了两个概念:
- 负载因子(load_factor),是hashtable的元素个数与hashtable的桶数之间比值;
- 最大负载因子(max_load_factor),是负载因子的上限
他们之间要满足:
load_factor = map.size() / map.buck_count() // load_factor 计算方式
load_factor <= max_load_factor // 限制条件
当hashtable中的元素个数与桶数比值load_factor >= max_load_factor时,hashtable就自动发生Rehash行为,来降低load_factor:
- 扩容。即使分配一块更大内存,来容纳更多的桶。
- 重新插入。按照上述插入步骤将原来桶中的buck_size个节点重新插入到新的桶中。
Rehash后,桶数增加了而元素个数不变,再次满足load_factor < max_load_factor条件。
Rehash
hashtable,由于要一直满足 load_factor <= max_load_factor ,限制着hash冲突程度,即每个桶的链表节点数不会无限制增加,整个hashtable的节点数达到一定程度就会Rehash,确保hashtable的搜索、删除的平均时间复杂度还是O(1)。
在std::unordered_map有个rehash函数,可以在任意时候使std::unordered_map发生Rehash,也可以等load_factor >= max_load_factor时自动发生。注意:
- 不同编译器的扩容策略不同,因此不编译器Rehash后桶的个数不一致很正常。
- 目前msvc和g++中的
max_load_factor字段默认值都是1。
下面以msvc编译触发rehash行为。
///@brief 向 @c map 中添加 n 个int类型值
void insert_n(std::unordered_map<int, int>& map, int start, int n) {
for (int idx = start; idx < start + n; ++idx) {
map.insert({ idx, idx });
}
std::cout << "bucket_cout: " << map.bucket_count() // 桶的个数
<< "|size: " << map.size() // 元素个数
<< "|load_factor: " << map.load_factor() << '\n'; // 负载因子
}
int main(int argc, char* const argv[]) {
std::unordered_map<int, int> map;
insert_n(map, 0, 0); // 初始化状态
insert_n(map, 0, 1);
insert_n(map, 1, 3);
insert_n(map, 3, 4);
insert_n(map, 7, 1); // 满负载
insert_n(map, 8, 1); // Rehash
return 0;
}
// 输出如下:
bucket_cout: 8|size: 1|load_factor: 0.125
bucket_cout: 8|size: 4|load_factor: 0.5
bucket_cout: 8|size: 7|load_factor: 0.875
bucket_cout: 8|size: 8|load_factor: 1
bucket_cout: 64|size: 9|load_factor: 0.140625
下一节从STL源码角度解析上述过程,看看std::unordered_map的底层实现细节。