Python KNN k-邻近算法 手动实现及分析 分类、回归、糖尿病预测实战

Python KNN k-邻近算法

算法原理

\qquad k-邻近算法的核心思想是未标记样本的类别，由距离其最近的k个邻近投票来决定。
\qquad 假设，我们有一个已经标记的数据集，即已经知道了数据集中每个样本所属的类别。此外，有一个未标记的数据样本，我们的任务是预测出这个数据样本所属的类别。k-邻近算法的原理是，计算待标记的数据样本和数据集中每个样本的距离，取距离最近的k个样本。待标记的数据样本所属的类别，就由这 $k$ 个距离最近的样本投票产生。

算法优缺点

\qquad 优点：准确性高，对异常值和噪声有较高的容忍度。
\qquad 缺点：计算量较大，对内容的需求较大。
从算法原理可以看出来，每次对一个未标记样本进行分类时，都需要全部计算一遍距离。

算法参数

\qquad 其算法参数是 $k$，参数选择需要根据数据来决定。$k$ 值越大，模型的偏差越大，对噪声数据越不敏感，当 $k$ 值很大时，可能造成模型欠拟合； $k$ 值越小，模型的方差就会越大，当 $k$ 值太小，就会造成模型过拟合。

算法的变种

\qquad k-邻近算法有一些变种，其中之一就是可以增加邻居的权重。默认情况下，在计算距离时，都是使用相同权重。实际上，我们可以针对不同的邻居指定不同的距离权重，如距离越近权重越高。这个可以通过指定算法的 weights 参数来实现。
\qquad 另一种变种是，使用一定半径内的点取代距离最近的 $k$ 个点。在 scikit-learn 里，RadiusNeighborsClassifier 类实现了这个算法的变种。当数据采样不均匀时，该算法变种可以取得更好的性能。

手动实现KNN k-邻近算法

代码及数据下载地址：

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
import operator
import matplotlib
from mpl_toolkits.mplot3d import Axes3D
import time

def createDataSet():
    group = np.array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
    labels = ['A', 'A', 'B', 'B']
    return group, labels

# K-近邻算法构造第一个分类器
def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]                          # 数据行数
    diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet      # 欧式距离
    sqDiffMat = diffMat ** 2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances ** 0.5
    sortedDistIndicies = np.argsort(distances)              # 对距离排序，得到索引
    classCount = {}                                         # 开字典用于类别数量
    for i in range(k):                                      # 遍历前k个最小的数据
        voteIlabel = labels[sortedDistIndicies[i]]          # 得到label
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1  # 相当于桶排序，+
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse= True)
    # 对票数进行排序，由于排序完从小到大，将其倒序，然后即票数最多的在字典中的第一个，[0][0]取label
    return sortedClassCount[0][0]                           # 返回预测类别

# 距离加权KNN算法的实现,权为距离平方的倒数
def addWeightClassify(inX, dataSet, labels, k):
    classCount = {}
    row = dataSet.shape[0]
    column = dataSet.shape[1]
    diffNdarray = dataSet - np.tile(inX, (row, 1))
    sqDiffNdarray = diffNdarray ** 2
    distance = np.sum(sqDiffNdarray,axis=1)
    sortedDistIndicies = np.argsort(distance)
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        if distance[sortedDistIndicies[i]] == 0:
            distance[sortedDistIndicies[i]] = 0.00000000001
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 * (1/((distance[sortedDistIndicies[i]])**2))
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse = True)
    return sortedClassCount[0][0]

# 从txt2中读取数据集
def file2Ndarray(filename):
    dataNdarray = np.loadtxt(filename)                      # 读取数据到数组
    classLabelVector = dataNdarray[:, -1]                   # 最后一列为类别
    dataNdarray = np.delete(dataNdarray, -1, axis = 1)      # 删除掉最后一纵列
    return dataNdarray, classLabelVector                    # 返回数据集+类别集

# 从txt1中读取数据集
def file1Ndarray(filename):
    fr = open(filename)
    arrayOLines = fr.readlines()
    row = len(arrayOLines)
    column = len(arrayOLines[0].strip().split(','))
    returnNdarray = np.array(np.zeros((row, column - 1)))
    classLabelVector = []
    index = 0
    for line in arrayOLines:                                # 数据集每行内容
        line = line.strip()                                 # 去除尾部空格
        listFromLine = line.split(',')                     # 去除中间空格,返回列表
        returnNdarray[index, :] = listFromLine[0:column-1]
        classLabelVector.append(listFromLine[column-1])
        index += 1
    return returnNdarray, classLabelVector

# 特征值归一化
def autoNorm(dataSet):
    columns = dataSet.shape[1]
    normDataSet = np.zeros((dataSet.shape[0], dataSet.shape[1]))
    for column in range(columns):
        minValue = np.min(dataSet[:,column])
        maxValue = np.max(dataSet[:,column])
        ranges = maxValue - minValue
        normDataSet[:, column] = (dataSet[:, column] - (np.tile(minValue, (dataSet.shape[0], 1))[:, 0]))\
                                 /(np.tile(ranges, (dataSet.shape[0], 1))[:, 0])
    return normDataSet

# 交叉验证
def loadfile(filename, k, classfiy):
    fr = open(filename)
    arraylines = fr.readlines()
    row = len(arraylines)
    column = len(arraylines[0].strip().split(','))
    dataNdarray = np.array(np.zeros((row, column-1)))
    labelList = []
    index = 0
    for line in arraylines:
        line = line.strip().split(',')
        dataNdarray[index, :] = line[:column-1]
        labelList.append(line[-1])
        index += 1
    labelSet = set(labelList)
    labelSet = list(labelSet)
    arglabelList = []
    for i in range(len(labelList)):
        for j in range(len(labelSet)):
            if (labelList[i].__eq__(labelList[j])):
                arglabelList.append(j)
    correct = 0
    for i in range(100):
        randomList = []
        for j in range(int(row/10)):
            randomList.append(int(np.random.rand(1)[0] * row))
        randomList = set(randomList)
        randomList = list(randomList)
        randomListCount = len(randomList)
        otherList = []
        otherargLabelList = []
        for w in range(row):
            flag = 1
            for z in range(randomListCount):
                if(w == randomList[z]):
                    flag = 0
            if flag == 1:
                otherList.append(w)
                otherargLabelList.append(arglabelList[w])
        otherNdarray = dataNdarray[otherList[:],:]
        randomLabelList = []
        for w in range(randomListCount):
            randomLabelList.append(arglabelList[randomList[w]])
        count = 0
        for w in range(randomListCount):
            label = classfiy(dataNdarray[randomList[w], :], otherNdarray, otherargLabelList, k)
            for z in range(len(labelSet)):
                if(arglabelList[randomList[w]]==(label)):
                    count += 1
        correct += float(count/randomListCount)
    correct = correct/100
    print('k == '+str(k)+'   correctPercent: '+str(correct * 100) + '%')
    return correct

# 绘图
def draw(x, y, labels, str):
    plt.figure(figsize=(8,5))
    plt.scatter(x, y,c =labels, s = 20)
    plt.xlabel(str[0])
    plt.ylabel(str[4])
    plt.title(str)
    plt.show()

# 绘制3D图
def draw3D(x, y, z, labels, str):
    ax = plt.subplot(111, projection = '3d')
    flag = []
    for i in range(len(labels)):
        flag.append(int(labels[i]))
    ax.scatter(x, y, z, c = flag)
    ax.set_zlabel('Z')
    ax.set_ylabel('Y')
    ax.set_xlabel('X')
    ax.set_title('x-y-z' + str)
    plt.show()

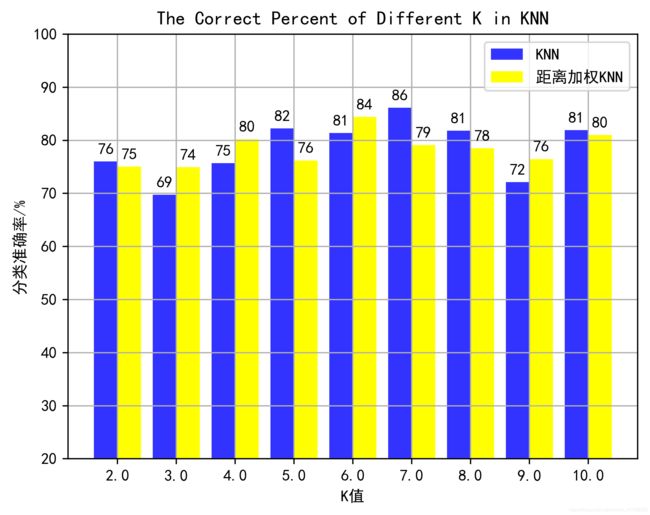
# 绘制条形图
def drawHist(dataSet1, dataSet2):
    dataSet1[:, 1] = dataSet1[:, 1] * 100
    dataSet2[:, 1] = dataSet2[:, 1] * 100
    matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 用黑体显示中文
    matplotlib.rcParams['axes.unicode_minus'] = False    # 正常显示负号
    label_list = dataSet1[:, 0]                          # X坐标
    height_list1 = dataSet1[:, 1]                        # 第一个Y坐标
    height_list2 = dataSet2[:, 1]                        # 第二个Y坐标
    x = np.arange(len(height_list1))
    rects1 = plt.bar(x, height = height_list1, width = 0.4, alpha = 0.8, color = 'blue', label="KNN")
    rects2 = plt.bar(x + 0.4, height=height_list2, width=0.4, color = 'yellow', label='距离加权KNN')
    plt.ylabel('分类准确率/%')
    plt.xlabel('K值')
    plt.ylim(20,100)
    plt.xticks([index + 0.2 for index in x], label_list)    # x轴刻度显示值
    plt.title('The Correct Percent of Different K in KNN')  # 标题
    plt.grid(True)                      #   网格
    plt.legend()                        #   图例
    for rect in rects1:                 #   编辑文本
        height = rect.get_height()
        plt.text(rect.get_x() + rect.get_width() / 2, height + 1, str(int(height)), ha="center", va="bottom")
    for rect in rects2:
        height = rect.get_height()
        plt.text(rect.get_x() + rect.get_width() / 2, height + 1, str(int(height)), ha="center", va="bottom")
    #plt.savefig('The Correct Percent of Different K in KNN.png', dpi=400, bbox_inches='tight')
    plt.show()

def main():
    k = 3
    tick1 = time.time()
    kDataSet1 = np.array(np.zeros((9, 2)))
    kDataSet2 = np.array(np.zeros((9, 2)))
    print('KNN分类：')
    for i in range(2, 11):
        correctPercent = loadfile('Iris.txt', i, classify0)
        kDataSet1[i-2, :] = i, correctPercent
    print('距离加权KNN：')
    for i in range(2, 11):
        correctPercent = loadfile('Iris.txt', i, addWeightClassify)
        kDataSet2[i-2, :] = i, correctPercent
    drawHist(kDataSet1, kDataSet2)
    '''
    group, labels = createDataSet()
    # draw(group, labels)
    if group.shape[0] <= k:
        k = group.shape[0]
    predictLabel = classify0(np.array([0.2, 0.2]), group, labels, k)
    '''

    dataNdarray, classLabelVector = file2Ndarray('datingTestSet2.txt')
    x = dataNdarray[:, 0]
    y = dataNdarray[:, 1]
    z = dataNdarray[:, 2]
    draw(x, y, classLabelVector, 'x - y -- datingTestSet2')
    draw(y, z, classLabelVector, 'y - z -- datingTestSet2')
    draw(x, z, classLabelVector, 'x - z -- datingTestSet2')
    draw3D(x, y, z, classLabelVector, '-- datingTestSet2')

    dataNdarray, classLabelVector = file1Ndarray('Iris.txt')
    dataNdarray = autoNorm(dataNdarray)                               # 归一化特征值
    # addWeightClassify(dataNdarray[0], dataNdarray, classLabelVector, k)
    x = dataNdarray[:, 0]
    y = dataNdarray[:, 1]
    z = dataNdarray[:, 2]
    labelSet = set(classLabelVector)
    labelKey = list(labelSet)
    labelList = []
    for label in range(len(classLabelVector)):
        for key in range(len(labelKey)):
            if  classLabelVector[label].__eq__(labelKey[key]):
                labelList.append(key)
    draw(x, y, labelList, 'x - y -- Iris')
    draw(y, z, labelList, 'y - z -- Iris')
    draw(x, z, labelList, 'x - z -- Iris')
    draw3D(x, y, z, labelList,'-- Iris')
    tick2 = time.time()
    print('time = {}'.format(tick2 - tick1))

if __name__ == '__main__':
    main()

使用scikit-learn的KNN进行分类

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
# 生成数据
centers = [[-2, 2], [2, 2], [0, 4]]
X, y = make_blobs(n_samples=60, centers=centers, random_state=0, cluster_std=0.60)
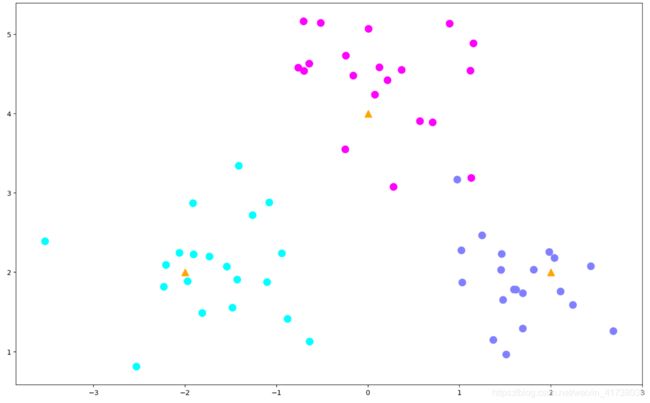
# 画出数据
plt.figure(figsize=(16, 10))
c = np.array(centers)
plt.scatter(X[:, 0], X[:, 1], c=y, s=100, cmap='cool');         # 画出样本
plt.scatter(c[:, 0], c[:, 1], s=100, marker='^', c='orange');   # 画出中心点

from sklearn.neighbors import KNeighborsClassifier
# 模型训练
k = 5
clf = KNeighborsClassifier(n_neighbors=k)
clf.fit(X, y);
# 进行预测
X_sample = [0, 2]
X_sample = np.array(X_sample).reshape(1, -1)
y_sample = clf.predict(X_sample);
neighbors = clf.kneighbors(X_sample, return_distance=False);
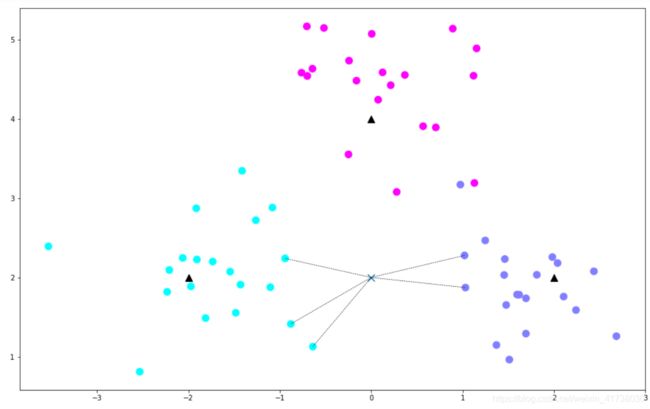
# 画出示意图
plt.figure(figsize=(16, 10))
plt.scatter(X[:, 0], X[:, 1], c=y, s=100, cmap='cool')    # 样本
plt.scatter(c[:, 0], c[:, 1], s=100, marker='^', c='k')   # 中心点
plt.scatter(X_sample[0][0], X_sample[0][1], marker="x", 
            s=100, cmap='cool')    # 待预测的点

for i in neighbors[0]:
    # 预测点与距离最近的 5 个样本的连线
    plt.plot([X[i][0], X_sample[0][0]], [X[i][1], X_sample[0][1]], 
             'k--', linewidth=0.6);

从下图，我们可以清楚地看出k-邻近算法的原理：

使用scikit-learn的KNN进行回归拟合

\qquad 分类问题的预测值是离散的，我们也可以用k-邻近算法在连续区间内对数值进行预测，进行回归拟合。
在 scikit-learn 里，使用 k-邻近算法进行回归拟合的算法是 sklearn.neighbors.KNeighborsRegressor类。
\qquad （1）生成数据集，它在余弦曲线的基础上加入了噪声：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# 生成训练样本
n_dots = 40
X = 5 * np.random.rand(n_dots, 1)
y = np.cos(X).ravel()

# 添加一些噪声
y += 0.2 * np.random.rand(n_dots) - 0.1

\qquad （2）使用 KNeightborsRegressor 来训练模型：

# 训练模型
from sklearn.neighbors import KNeighborsRegressor
k = 5
knn = KNeighborsRegressor(k)
knn.fit(X, y);

\qquad 我们要怎么样来进行回归拟合呢？
\qquad 一个方法是，在 $X$ 轴上的指定区间内生成足够多的点，针对这些足够密集的点，使用训练出来的模型进行预测，得到预测值， y_pred，然后在坐标轴上，把所有的预测点链接起来，就这样画出了拟合曲线。
\qquad 我们针对足够多密集的点继续预测：

# 生成足够密集的点并进行预测
T = np.linspace(0, 5, 500)[:, np.newaxis]
y_pred = knn.predict(T)
knn.score(X, y)

\qquad 可以用 score() 方法计算拟合曲线针对训练样本的拟合准确性，在笔者的环境下输出结果为：

0.9817739454731815

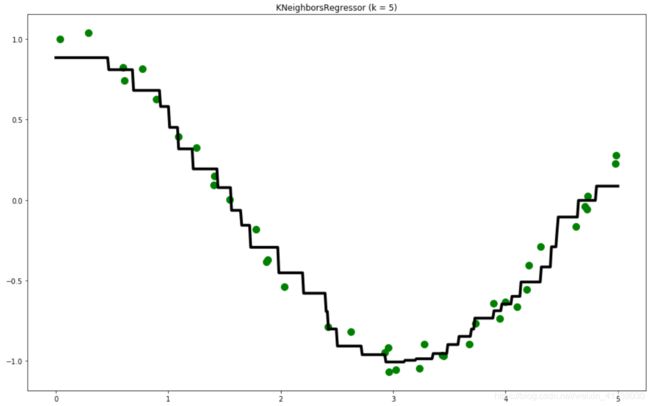
\qquad （3）把这些预测点连起来，构成拟合曲线：

# 画出拟合曲线
plt.figure(figsize=(16, 10))
plt.scatter(X, y, c='g', label='data', s=100)         # 画出训练样本
plt.plot(T, y_pred, c='k', label='prediction', lw=4)  # 画出拟合曲线
plt.axis('tight')
plt.title("KNeighborsRegressor (k = %i)" % k)
plt.show()

\qquad 最终生成的拟合曲线以及训练样本数据如图：

实例：糖尿病预测

加载数据

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# 加载数据
data = pd.read_csv('datasets/pima-indians-diabetes/diabetes.csv')
print('dataset shape {}'.format(data.shape))
data.head()

data.groupby("Outcome").size()

Outcome
0    500
1    268
dtype: int64

\qquad 其中阴性样本500例，阳性样本268例。接着，需要对数据集进行简单处理，把 8 个特征值分离出来，作为训练数据集，把 Outcome 列分离出来作为目标值。然后，把数据集划分为训练数据集和测试数据集。

X = data.iloc[:, 0:8]
Y = data.iloc[:, 8]
print('shape of X {}; shape of Y {}'.format(X.shape, Y.shape))

模型比较

\qquad 使用普通的 k-均值算法、带权重 k-均值算法以及指定半径的 k-均值算法分别对数据集进行拟合并计算评分：

from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)
from sklearn.neighbors import KNeighborsClassifier, RadiusNeighborsClassifier

# 构建三个模型
models = []
models.append(("KNN", KNeighborsClassifier(n_neighbors=2)))
models.append(("KNN with weights", KNeighborsClassifier(
    n_neighbors=2, weights="distance")))
models.append(("Radius Neighbors", RadiusNeighborsClassifier(
    n_neighbors=2, radius=500.0)))

# 分别训练3个模型，并计算评分
results = []
for name, model in models:
    model.fit(X_train, Y_train)
    results.append((name, model.score(X_test, Y_test)))
for i in range(len(results)):
    print("name: {}; score: {}".format(results[i][0],results[i][1]))

\qquad 笔者计算机的输出如下：

name: KNN; score: 0.6948051948051948
name: KNN with weights; score: 0.6623376623376623
name: Radius Neighbors; score: 0.6168831168831169

\qquad 权重算法，我们选择了距离越近，权重越高。RadiusNeighborsClassifier 模型的半径，选择了500。从输出可以看出，普通的 k-均值算法性能还是最好。问题来了，这个判断准确么？答案是不准确的。因为我们的训练样本和测试样本是随机分配的，不同的训练样本和测试样本组合可能导致计算出来的算法准确性是有差异的。
\qquad 怎么样更准确地比较算法准确性呢? 一个方法是，多次随机分配训练数据集合交叉验证数据集，然后求模型准确性评分的平均值。所幸，我们不需要从头实现这个过程，scikit-learn 提供了 KFold 和 cross_val_score() 函数来处理这种问题：

from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score

results = []
for name, model in models:
    kfold = KFold(n_splits=10)
    cv_result = cross_val_score(model, X, Y, cv=kfold)
    results.append((name, cv_result))
for i in range(len(results)):
    print("name: {}; cross val score: {}".format(
        results[i][0],results[i][1].mean()))

\qquad 上述代码中，我们通过 KFlod 把数据集分成10份，其中1份会作为交叉验证数据集来计算模型准确性，剩余的9份作为训练数据集。cross_val_score() 函数总共计算出 10次不同训练数据集合交叉验证数据集组成得到的模型准确性评分，最后求平均值。这样的评价结果相对更加准确一些。
\qquad 输出结果为：

name: KNN; cross val score: 0.7147641831852358
name: KNN with weights; cross val score: 0.6770505809979495
name: Radius Neighbors; cross val score: 0.6497265892002735

模型训练及分析

\qquad 看起来，还是普通的 k-均值算法性能更优一些。接下来，我们就使用普通的 k-均值算法模型对数据集进行训练，并查看对训练样本的拟合情况以及对测试样本的预测准确性情况：

knn = KNeighborsClassifier(n_neighbors=2)
knn.fit(X_train, Y_train)
train_score = knn.score(X_train, Y_train)
test_score = knn.score(X_test, Y_test)
print("train score: {}; test score: {}".format(train_score, test_score))

KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=None, n_neighbors=2, p=2,
           weights='uniform')
train score: 0.8420195439739414; test score: 0.6493506493506493

\qquad 从这个输出中可以看到两个问题。一是对训练样本的拟合情况不佳，评分才 0.84 多一些，这说明算法模型太简单了，无法很好地拟合训练样本。二是模型的准确性欠佳，不到 73% 的预测准确性。我们可以进一步画出学习曲线，证实结论。

from sklearn.model_selection import ShuffleSplit
from common.utils import plot_learning_curve

knn = KNeighborsClassifier(n_neighbors=2)
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
plt.figure(figsize=(10, 6))
plot_learning_curve(plt, knn, "Learn Curve for KNN Diabetes", 
                    X, Y, ylim=(0.0, 1.01), cv=cv);

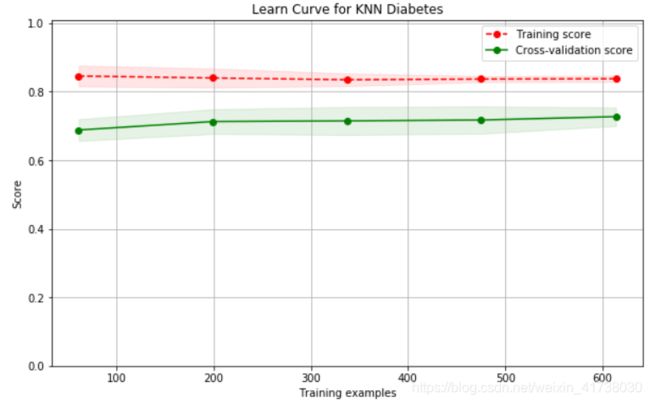
\qquad 从图中可以看出来，训练样本评分较低，且测试样本与训练样本距离较大，这是经典的欠拟合现象。 k-均值算法没有更好的措施来解决欠拟合问题，读者学完本书的其他章节后，可以试着用其他算法（如逻辑回归算法、支持向量机等）来对比不同模型的准确性情况。

特征选择及数据可视化

\qquad 读者不禁要问，有没有直观的方法，来揭示出为什么 k-均值算法不是针对这一问题的好模型？一个方法是把数据画出来，课室我们有8个特征，无法在这么高的纬度里画出数据，并直观观察。一个解决方法是特征选择，即只选择2个与输出相关性最大的特征，这样就可以在二维平面上画出输入特征值与输出值的关系了。
\qquad 所幸，scikit-learn 在 sklearn.feature_selection 包里提供了丰富的特征选择方法。我们使用SelectKBest 来选择相关性最大的两个特征：

from sklearn.feature_selection import SelectKBest

selector = SelectKBest(k=2)
X_new = selector.fit_transform(X, Y)
X_new[0:5]

把相关性最大的两个特征放在 X_new 变量里，同时输出了前 5 个数据样本。输出结果为：

array([[148. ,  33.6],
       [ 85. ,  26.6],
       [183. ,  23.3],
       [ 89. ,  28.1],
       [137. ,  43.1]])

\qquad 读者可能会好奇，相关性最大的特征到底是哪两个？对比一下本节开头的数据即可知道，它们分别是 Glucose（血糖浓度）和 BMI（身体质量指数）。

\qquad 我们来看看，如果只使用这2个相关性最高的特征的话，3种不同的 k-均值算法那个准确性更高：

results = []
for name, model in models:
    kfold = KFold(n_splits=10)
    cv_result = cross_val_score(model, X_new, Y, cv=kfold)
    results.append((name, cv_result))
for i in range(len(results)):
    print("name: {}; cross val score: {}".format(
        results[i][0],results[i][1].mean()))

\qquad 这次使用 X_new 作为输入，笔者计算机的输出结果为：

name: KNN; cross val score: 0.725205058099795
name: KNN with weights; cross val score: 0.6900375939849623
name: Radius Neighbors; cross val score: 0.6510252904989747

\qquad 从输出可以看出来，还是普通的 k-均值模型准确性较高，其准确性也达到了将近 73%，与所有特征拿来一块儿训练的准确性差不多。这也侧面证明了 SelectKBest 特征选择的准确性。
\qquad 回到目标上来，我们是想看看为什么 k-均值无法很好地拟合训练样本。现在我们只有 2 个特征，可以很方便地在二维坐标上画出所有的训练样本，观察这些数据的分布情况：

\qquad 横坐标是血糖值，纵坐标是BMI值，反应身体肥胖情况。从图中可以看出来，在中间数据集密集的区域，阴性样本和阳性样本几乎重叠在一起了。假设现在有一个待预测的样本在中间密集区域，它的阳性邻居多还是阴性邻居多呢？这个真的很难说，这样就可以直观地看出， k-均值算法在这个糖尿病预测问题上，无法达到很高的预测准确性。