决策边界绘制函数plot_decision_boundary()和plt.contourf函数详解
在做吴恩达老师的深度学习课程作业时,发现决策边界函数不好理解plot_decision_boundary(model , X , y)。将此函数理解记录下:
作业地址:https://blog.csdn.net/u013733326/article/details/79702148
绘制梯度下降算法图形或是决策边界,核心便在于知道plt.contourf函数的用法
plt.contourf函数
这里参考https://blog.csdn.net/qq_44669578/article/details/103348076?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-8.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-8.nonecase
plt.contourf用来画出不同分类的边界线,也常常用来绘制等高线
1.生成数据点
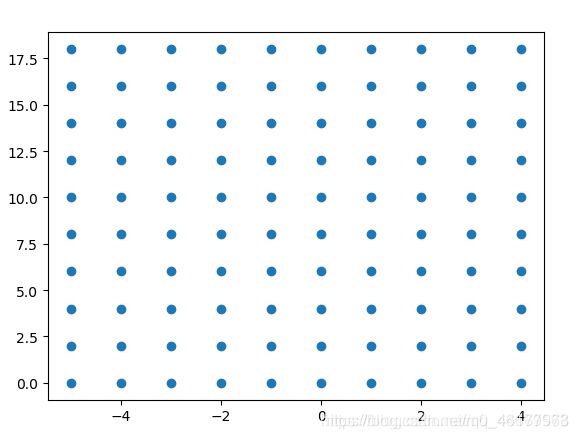
x = np.arange(-5, 5, 1)
y = np.arange(0, 20, 2)
xx, yy = np.meshgrid(x, y)
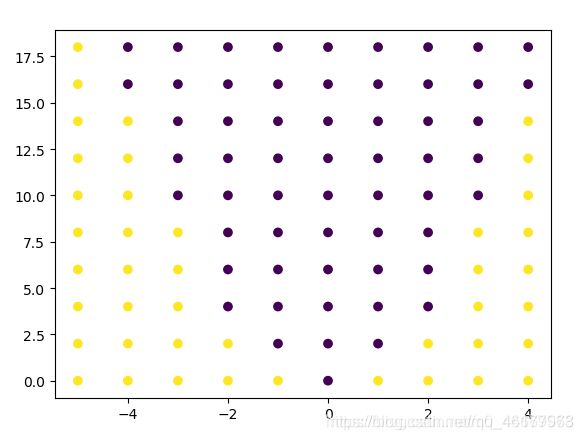
z = np.square(xx) - yy > 0
plt.contourf(xx, yy, z, cmap=plt.cm.Spectral)
plt.scatter(xx, yy, c=z)
plt.show()
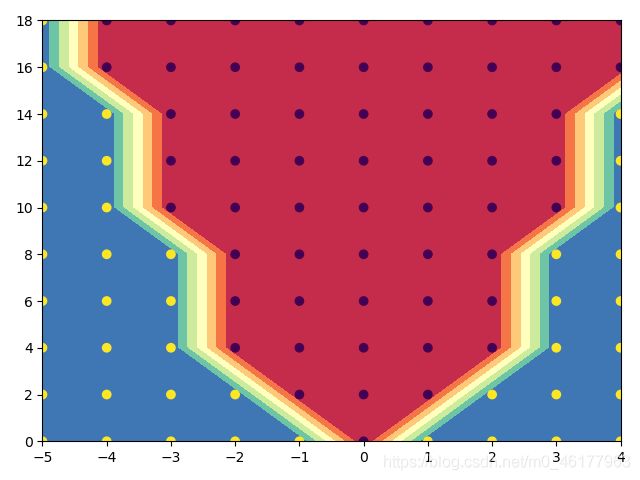
如果点设置得更密集一点,分界处会更光滑,可以看到完整的抛物线
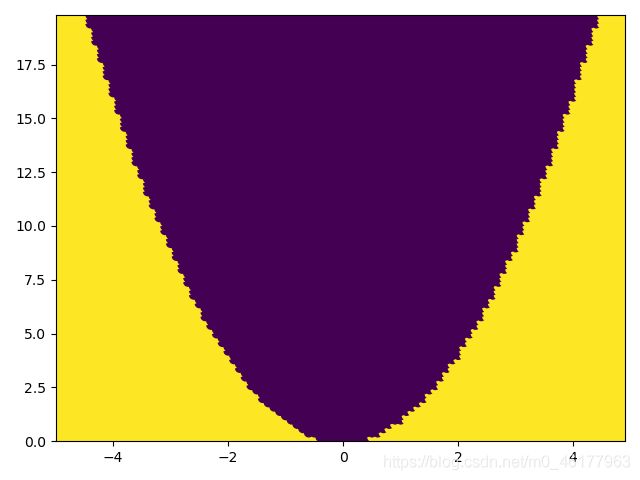
完整代码
x = np.arange(-5, 5, 0.1)
y = np.arange(0, 20, 0.2)
xx, yy = np.meshgrid(x, y)
z = np.square(xx) - yy > 0
#plt.cm.Spectral,在这的意思就是颜色会随Z的值变化
plt.contourf(xx, yy, z, cmap=plt.cm.Spectral)
plt.scatter(xx, yy, c=z)
plt.show()
2.plot_decision_boundary()函数理解
先附上完整代码
def plot_decision_boundary(model, X, y):
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
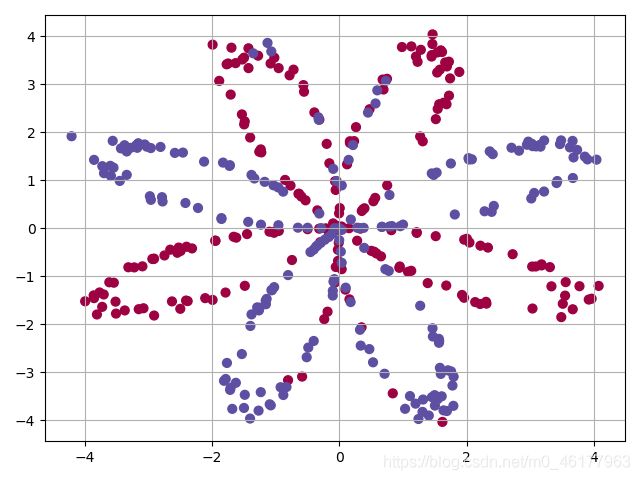
plt.scatter(X[0, :], X[1, :], c=np.squeeze(y), cmap=plt.cm.Spectral)
调用训练好的模型
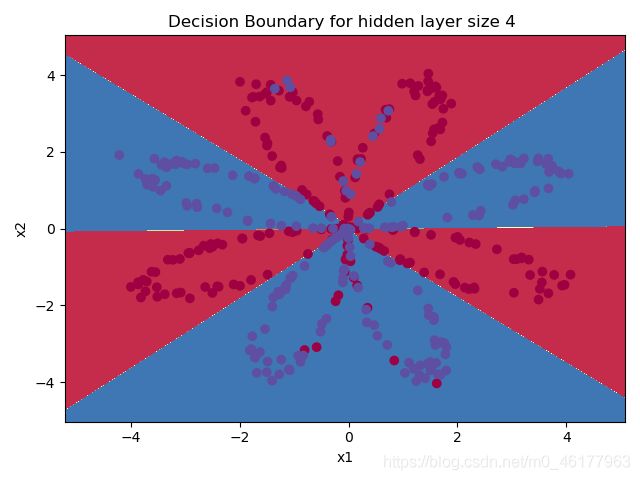
绘制此决策边界的思路是:首先已经通过了神经网络拟合出了输入特征和标签的函数关系,然后生成间距很小的网格覆盖这些点(函数中用h表示网格点之间的距离),将网格的坐标送入训练好的神经网络,神经网络会为每个网格坐标输出一个预测值,注意,这个网格点非常多,占满了整张图,图中的红色和蓝色其实就是经过预测后的网格点所填充的颜色,以预测值0.5进行划分,预测值为0.5的这条线也即为红点和蓝点的区分线。
首先按照样本大小,以0.01的间距生成网格
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
然后用训练好的模型对网格上的所有的点进行预测,返回一个只含0/1的矩阵
然后改变矩阵Z的形状,因为在contourf函数中,当 X,Y,Z 都是 2 维数组时,它们的形状必须相同。
Z = model(np.c_[xx.ravel(), yy.ravel()]) #ravel()函数将多维降至一维,默认行优先
Z = Z.reshape(xx.shape)
然后画图,plt.cm.Spectral,在这的意思就是颜色会随Z的值变化
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(X[0, :], X[1, :], c=np.squeeze(y), cmap=plt.cm.Spectral)