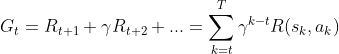【深度强化学习】(2) Double DQN 模型解析，附Pytorch完整代码
大家好，今天和大家分享一个深度强化学习算法 DQN 的改进版 Double DQN，并基于 OpenAI 的 gym 环境库完成一个小游戏，完整代码可以从我的 GitHub 中获得：
https://github.com/LiSir-HIT/Reinforcement-Learning/tree/main/Model
1. 算法原理
1.1 DQN 原理回顾
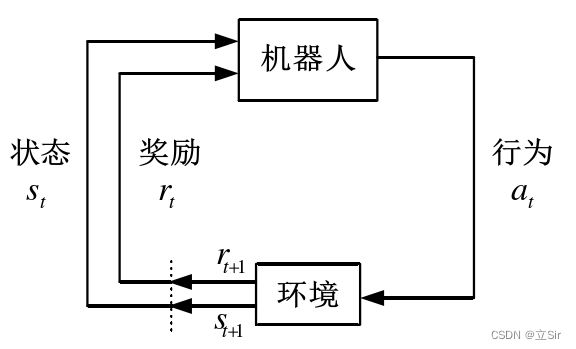
DQN 算法的原理是指导机器人不断与环境交互，理解最佳的行为方式，最终学习到最优的行为策略，机器人与环境的交互过程如下图所示。
机器人与环境的交互过程是机器人在 
时刻，采取动作 
并作用于环境，然后环境从 时刻状态 
转变到 
时刻状态 
，同时奖励函数对 进行评价得到奖励值 
。机器人根据 不断优化行为轨迹，最终学习到最优的行为策略。
整个强化学习过程可简化为马尔可夫决策过程（MDP）。其中所有状态均具备马尔可夫性。MDP 可用一个五元组 
表示，各元素意义如下：
（1）S 是有限状态集合，即机器人在环境中探索到的所有可能状态。 表示机器人在 t 时刻的状态。
（2）A 是有限动作集合，即智能体根据 采取的所有可能动作集合。 表示机器人在t 时刻状态采取的行为
（3）P 是状态转移概率，定义如下：![P_{s_{t+1}}^a = P[S_{t+1}=s_{t+1}|S_t=s, A_t=a]](http://img.e-com-net.com/image/info8/692593c674d74f7f907c053905023007.gif){kind=small}
（4）R 是奖励函数，即机器人基于 采取 后获得的期望奖励，定义如下：![R_s^a = E[R_{t+1}|s_{t+1}|S_t=s, A_t=a]](http://img.e-com-net.com/image/info8/67372a42a49744a5b1c2223a0b00f853.gif){kind=small}
（5）γ 代表折扣因子，值域 [0,1]，即未来的期望奖励在当前时刻的价值比例。
MDP 中，价值函数包括状态价值函数和动作价值函数。动作价值函数（Q 函数）表示在策略 
的指导下，根据状态 
，采取行为 
所获得的期望回报。策略 表示状态到行为的映射，相当于机器人的决策策略，并根据不同的状态选择不同的行为，即 
。机器人在策略 的指导下，Q 函数的定义如下：
![Q_\pi (s,a)=E_\pi [G_t|S_t=s,A_t=a]](http://img.e-com-net.com/image/info8/c050fb666d404491b64f0e8e66a7cd32.gif){kind=small}
式中 
表示折扣奖励，定义如下：
式中 
随训练过程迭代减小， 越小表示未来的奖励对当前时刻的奖励影响越小。
Q 函数的贝尔曼方程表示如下：
![Q_\pi (s_t,a_t)=E[R(s_t,a_t)+\gamma E_{a_{t+1\sim \pi }}Q_\pi (s_{t+1}, a_{t+1})]](http://img.e-com-net.com/image/info8/9f6ee7054c984d30bf8facbbe3aa8ea7.gif){kind=small}
式中，
表示机器人在 时采取 所获得的即时奖励，等式右侧第二项表示机
器人执行策略 产生的未来累计奖励的期望。
通过选取最大动作价值函数求解最优行为策略的公式表示如下：
DQN 算法通过行为的奖励值构造算法训练的标签，并且其中的经验回放（Experience Replay）和目标网络有效的解决了数据相关性和非静态分布的问题。DQN 算法的结构示意图如下。
DQN 的网络结构由目标网络和估计网络组成，这两个网络的结构相同但参数不同。估计网络具有最新的网络参数，计算当前状态-动作对的价值，并定期更新目标网络的参数，使其计算目标 Q 值。双网络结构打破了数据之间的相关性，使DQN 学习不同的数据分布。经验回放部分储存了智能体（机器人）的历史行为信息，其中包括多组行为序列对 
，即当前时刻状态 s ，行为 a ，奖励 r 以及下一时刻状态 s'。当 DQN 算法更新时，随机从经验池中抽取部分行为序列对进行经验回放，这种方式解决了经验池中数据相关性强和非静态分布导致的模型泛化能力差的问题。
DQN 算法通过贪婪法直接获得目标 Q 值，贪婪法通过最大化方式使 Q 值快速向可能的优化目标收敛，但易导致过估计Q 值的问题，使模型具有较大的偏差。DQN 算法过估计 Q 值的问题不适合机器人操作行为的研究，采用 Double DQN 算法解耦动作的选择和目标 Q 值的计算，以解决过估计 Q 值的问题。
1.2 Double DQN 原理
Double DQN 算法是 DQN 算法的改进版本，解决了 DQN 算法过估计行为价值的问题。DQN 算法中，某一时刻状态为非终止状态时，目标 Q 值的计算公式如下所示：
Double DQN 算法不直接通过最大化的方式选取目标网络计算的所有可能 Q 值，而是首先通过估计网络选取最大 Q 值对应的动作，公式表示如下：
然后目标网络根据 
计算目标 Q 值，公式表示如下：
最后将上面两个公式结合，目标 Q 值的最终表示形式如下：
目标是最小化目标函数，即最小化估计 Q 值和目标 Q 值的差值，公式如下：
结合目标函数，损失函数定义如下：
Double DQN 的伪代码：
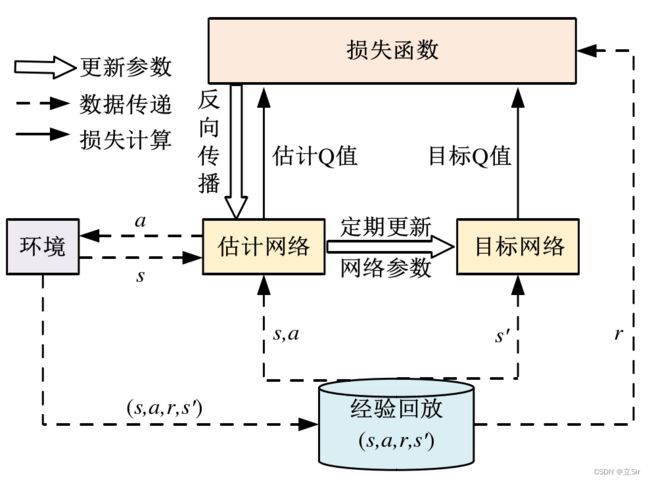
Double DQN 算法结构如下。在 Double DQN 框架中存在两个神经网络模型，分别是训练网络与目标网络。这两个神经网络模型的结构完全相同，但是权重参数不同；每训练一段之间后，训练网络的权重参数才会复制给目标网络。训练时，训练网络用于估计当前的 
，而目标网络用于估计 
，这样就能保证真实值 
的估计不会随着训练网络的不断自更新而变化过快。此外，DQN 还是一种支持离线学习的框架，即通过构建经验池的方式离线学习过去的经验。将均方误差 
作为训练模型的损失函数，通过梯度下降法进行反向传播，对训练模型进行更新；若干轮经验池采样后，再将训练模型的权重赋给目标模型，以此进行 Double DQN 框架下的模型自学习。
2. 代码实现
模型构建部分的代码如下：
import torch
from torch import nn
from torch.nn import functional as F
import numpy as np
import collections # 队列
import random
# ----------------------------------- #
#（1）经验回放池
# ----------------------------------- #
class ReplayBuffer:
def __init__(self, capacity):
# 创建一个队列，先进先出，队列长度不变
self.buffer = collections.deque(maxlen=capacity)
# 填充经验池
def add(self, state, action, reward, next_state, done):
self.buffer.append((state, action, reward, next_state, done))
# 随机采样batch组样本数据
def sample(self, batch_size):
transitions = random.sample(self.buffer, batch_size)
# 分别取出这些数据，*获取list中的所有值
state, action, reward, next_state, done = zip(*transitions)
# 将state变成数组，后面方便计算
return np.array(state), action, reward, np.array(next_state), done
# 队列的长度
def size(self):
return len(self.buffer)
# ----------------------------------- #
#（2）构造网络，训练网络和目标网络共用该结构
# ----------------------------------- #
class Net(nn.Module):
def __init__(self, n_states, n_hiddens, n_actions):
super(Net, self).__init__()
# 只有一个隐含层
self.fc1 = nn.Linear(n_states, n_hiddens)
self.fc2 = nn.Linear(n_hiddens, n_actions)
# 前向传播
def forward(self, x):
x = self.fc1(x) # [b,n_states]-->[b,n_hiddens]
x = self.fc2(x) # [b,n_hiddens]-->[b,n_actions]
return x
# ----------------------------------- #
#（3）模型构建
# ----------------------------------- #
class Double_DQN:
#（1）初始化
def __init__(self, n_states, n_hiddens, n_actions,
learning_rate, gamma, epsilon,
target_update, device):
# 属性分配
self.n_states = n_states
self.n_hiddens = n_hiddens
self.n_actions = n_actions
self.learning_rate = learning_rate
self.gamma = gamma
self.epsilon = epsilon
self.target_update = target_update
self.device = device
# 记录迭代次数
self.count = 0
# 实例化训练网络
self.q_net = Net(self.n_states, self.n_hiddens, self.n_actions)
# 实例化目标网络
self.target_q_net = Net(self.n_states, self.n_hiddens, self.n_actions)
# 优化器，更新训练网络的参数
self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=self.learning_rate)
#（2）动作选择
def take_action(self, state):
# numpy[n_states]-->[1, n_states]-->Tensor
state = torch.Tensor(state[np.newaxis, :])
# print('--------------------------')
# print(state.shape)
# 如果小于贪婪系数就取最大值reward最大的动作
if np.random.random() < self.epsilon:
# 获取当前状态下采取各动作的reward
actions_value = self.q_net(state)
# 获取reward最大值对应的动作索引
action = actions_value.argmax().item()
# 如果大于贪婪系数就随即探索
else:
action = np.random.randint(self.n_actions)
return action
#（3）获取每个状态对应的最大的state_value
def max_q_value(self, state):
# list-->tensor[3]-->[1,3]
state = torch.tensor(state, dtype=torch.float).view(1,-1)
# 当前状态对应的每个动作的reward的最大值 [1,3]-->[1,11]-->int
max_q = self.q_net(state).max().item()
return max_q
#（4）网络训练
def update(self, transitions_dict):
# 当前状态，array_shape=[b,4]
states = torch.tensor(transitions_dict['states'], dtype=torch.float)
# 当前状态的动作，tuple_shape=[b]==>[b,1]
actions = torch.tensor(transitions_dict['actions'], dtype=torch.int64).view(-1,1)
# 选择当前动作的奖励, tuple_shape=[b]==>[b,1]
rewards = torch.tensor(transitions_dict['rewards'], dtype=torch.float).view(-1,1)
# 下一个时刻的状态array_shape=[b,4]
next_states = torch.tensor(transitions_dict['next_states'], dtype=torch.float)
# 是否到达目标 tuple_shape=[b,1]
dones = torch.tensor(transitions_dict['dones'], dtype=torch.float).view(-1,1)
# 当前状态[b,4]-->当前状态采取的动作及其奖励[b,2]-->actions中是每个状态下的动作索引
# -->当前状态s下采取动作a得到的state_value
q_values = self.q_net(states).gather(1, actions)
# 获取动作索引
# .max(1)输出tuple每个特征的最大state_value及其索引，[1]获取的每个特征的动作索引shape=[b]
max_action = self.q_net(next_states).max(1)[1].view(-1,1)
# 下个状态的state_value。下一时刻的状态输入到目标网络，得到每个动作对应的奖励，使用训练出来的action索引选取最优动作
max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
# 目标网络计算出的，当前状态的state_value
q_targets = rewards + self.gamma * max_next_q_values * (1-dones)
# 预测值和目标值的均方误差损失
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))
# 梯度清零
self.optimizer.zero_grad()
# 梯度反传
dqn_loss.backward()
# 更新训练网络的参数
self.optimizer.step()
# 更新目标网络参数
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(
self.q_net.state_dict()) # 更新目标网络
# 迭代计数+1
self.count += 1
3. 案例实现
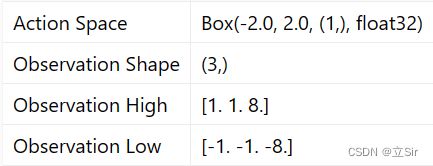
我们使用 OpenAI 中的重力摆来验证模型，动作是连续型，代表力矩；状态包含三个；目的是让杆子竖直。
环境交互和训练代码如下：
import torch
import numpy as np
import gym
from tqdm import tqdm
import matplotlib.pyplot as plt
from parsers import args
from RL_brain import ReplayBuffer, Double_DQN
# GPU运算
device = torch.device("cuda") if torch.cuda.is_available() \
else torch.device("cpu")
# ------------------------------- #
#（1）加载环境
# ------------------------------- #
env = gym.make("Pendulum-v1", render_mode="human")
n_states = env.observation_space.shape[0] # 状态数 3
act_low = env.action_space.low # 最小动作力矩 -2
act_high = env.action_space.high # 最大动作力矩 +2
n_actions = 11 # 动作是连续的[-2,2]，将其离散成11个动作
# 确定离散动作区间后，确定其连续动作
def dis_to_con(discrete_action, n_actions):
# discrete_action代表动作索引
return act_low + (act_high-act_low) * (discrete_action/(n_actions-1))
# 实例化经验池
replay_buffer = ReplayBuffer(args.capacity)
# 实例化 Double-DQN
agent = Double_DQN(n_states,
args.n_hiddens,
n_actions,
args.lr,
args.gamma,
args.epsilon,
args.target_update,
device
)
# ------------------------------- #
#（2）模型训练
# ------------------------------- #
return_list = [] # 记录每次迭代的return，即链上的reward之和
max_q_value = 0 # 最大state_value
max_q_value_list = [] # 保存所有最大的state_value
for i in range(10): # 训练几个回合
done = False # 初始，未到达终点
state = env.reset()[0] # 重置环境
episode_return = 0 # 记录每回合的return
with tqdm(total=10, desc='Iteration %d' % i) as pbar:
while True:
# 状态state时做动作选择，返回索引
action = agent.take_action(state)
# 平滑处理最大state_value
max_q_value = agent.max_q_value(state) * 0.005 + \
max_q_value * 0.995
# 保存每次迭代的最大state_value
max_q_value_list.append(max_q_value)
# 将action的离散索引连续化
action_continuous = dis_to_con(action, n_actions)
# 环境更新
next_state, reward, done, _, _ = env.step(action_continuous)
# 添加经验池
replay_buffer.add(state, action, reward, next_state, done)
# 更新状态
state = next_state
# 更新每回合的回报
episode_return += reward
# 如果经验池超数量过阈值时开始训练
if replay_buffer.size() > args.min_size:
# 在经验池中随机抽样batch组数据
s, a, r, ns, d = replay_buffer.sample(args.batch_size)
# 构造训练集
transitions_dict = {
'states': s,
'actions': a,
'next_states': ns,
'rewards': r,
'dones': d,
}
# 模型训练
agent.update(transitions_dict)
# 到达终点就停止
if done is True: break
# 保存每回合的return
return_list.append(episode_return)
pbar.set_postfix({
'step':
agent.count,
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
# ------------------------------- #
#（3）绘图
# ------------------------------- #
plt.subplot(121)
plt.plot(return_list)
plt.title('return')
plt.subplot(122)
plt.plot(max_q_value_list)
plt.title('max_q_value')
plt.show()