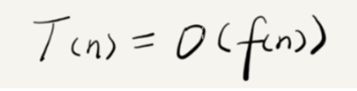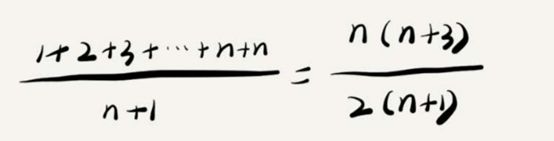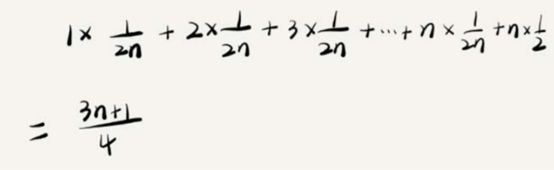数据结构的时间复杂度和空间复杂度

为什么需要时间复杂度和空间复杂度

 

你可能会有些疑惑，我把代码跑一遍，通过统计、监控，就能得到算法执行的时间和占用的内存大小。为什么还要做时间、空间复杂度分析呢？这种分析方法能比我实实在在跑一遍得到的数据更准确吗？

首先，我可以肯定地说，你这种评估算法执行效率的方法是正确的。很多数据结构和算法书籍还给这种方法起了一个名字，叫事后统计法。但是，这种统计方法有非常大的局限性。

1. 测试结果非常依赖测试环境

测试环境中硬件的不同会对测试结果有很大的影响。比如，我们拿同样一段代码，分别用Intel Core i9处理器和Intel Core i3处理器来运行，不用说，i9处理器要比i3处理器执行的速度快很多。还有，比如原本在这台机器上a代码执行的速度比b代码要快，等我们换到另一台机器上时，可能会有截然相反的结果。

2.测试结果受数据规模的影响很大

后面我们会讲排序算法，我们先拿它举个例子。对同一个排序算法，待排序数据的有序度不一样，排序的执行时间就会有很大的差别。极端情况下，如果数据已经是有序的，那排序算法不需要做任何操作，执行时间就会非常短。除此之外，如果测试数据规模太小，测试结果可能无法真实地反应算法的性能。比如，对于小规模的数据排序，插入排序可能反倒会比快速排序要快！

所以，我们需要一个不用具体的测试数据来测试，就可以粗略地估计算法的执行效率的方法。这就是我们今天要讲的时间复杂度、空间复杂度

 

时间复杂度

时间复杂度的最基本计算

这里有段非常简单的代码，求1,2,3…n的累加和。现在，我就带你一块来估算一下这段代码的执行时间。

这里我们把每执行一行的时间都规定为unit_time，那么下面的红字代码分别需要1个unit_time的执行时间，第蓝色代码都运行了n遍，所以需要2n*unit_time的执行时间，所以这段代码总的执行时间就是(2n+2)*unit_time。可以看出来，所有代码的执行时间T(n)与每行代码的执行次数成正比。

 

int cal(int n) {         int sum = 0;         int i = 1;         for (; i <= n; ++i) {             sum = sum + i;         }         return sum;     }

 

我们再来看这段代码。每一个蓝色代码都需要1个unit_time的执行时间，红色代码循环执行了n遍，需要2n * unit_time的执行时间，然后绿色代码循环执行了n*n遍，所以需要2*n*n*unit_time的执行时间。所以，整段代码总的执行时间T(n) = (2*n*n+2n+3)*unit_time，

void cal(int n) {         int sum = 0;         int i = 1;         int j = 1;         for (; i <= n; ++i) {             j = 1;             for (; j <= n; ++j) {                 sum = sum + i * j;             }         }     }

 

尽管我们不知道unit_time的具体值，但是通过这两段代码执行时间的推导过程，我们可以得到一个非常重要的规律，那就是，所有代码的执行时间T(n)与每行代码的执行次数n成正比。我们可以把这个规律总结成一个公式。注意，大O就要登场了！

这里T(n)我们已经讲过了，它表示代码执行的时间；n表示数据规模的大小；f(n)表示每行代码执行的次数总和。因为这是一个公式，所以用f(n)来表示。公式中的O，表示代码的执行时间T(n)与f(n)表达式成正比。

所以，第一个例子中的T(n) = O(2n+2)，第二个例子中的T(n) = O(2n*n+2n+3)。这就是大O时间复杂度表示法。大O时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

然后当n很大时，你可以把它想象成10000、100000。而公式中的低阶、常量、系数三部分并不左右增长趋势，所以都可以忽略。我们只需要记录一个最大量级就可以了，如果用大O表示法表示刚讲的那两段代码的时间复杂度，就可以记为：T(n) = O(n)； T(n) = O(n*n)。

时间复杂度的几条运算规则

通常会忽略掉公式里面的常量和低阶和系数

大O这种复杂度表示方法只是表示一种变化趋势。我们通常会忽略掉公式中的常量、低阶、系数，只需要记录一个最大阶的量级就可以了。所以，我们在分析一个算法、一段代码的时间复杂度的时候，也只关注循环执行次数最多的那一段代码就可以了。这段核心代码执行次数的n的量级，就是整段要分析代码的时间复杂度。就像下面的代码

 

其中蓝色代码都是常量级的执行时间，与n的大小无关，所以对于复杂度并没有影响。循环执行次数最多的是红色代码，所以这块代码要重点分析。前面我们也讲过，这两行代码都被执行了n次，所以总的时间复杂度就是O(n)(原本的是O(2n+2)，这里省下了2n前面的2系数和2n+2后面的常量2)

 

int cal(int n) {         int sum = 0;         int i = 1;         for (; i <= n; ++i) {             sum = sum + i;         }         return sum;     }

总复杂度等于量级最大的那段代码的复杂度

 

就像下面有三个for循环，所以准确来说此时时间复杂度就是O(2*n*n+2n+100*2+2+2+3+1)，其中2+2+3+1就是下面的蓝色代码，根据上面的规则，此时可以变成O(n*n+n)的， 但是随着n值的增长，比如增长到100000的时候，下面的就只有第三个for循环的复杂度最高了，所以此时O(n*n+n)就可以简单写成O(n*n)，，但是这个也不是必须要这样做，要随机应变，如果你的n的值已经确定不会达到100，那么此时的时间复杂度也应该是理解成O(n*n+n)的

 

int cal(int n) {         int sum_1 = 0;         int p = 1;         for (; p < 100; ++p) {             sum_1 = sum_1 + p;         }         int sum_2 = 0;         int q = 1;         for (; q < n; ++q) {             sum_2 = sum_2 + q;         }         int sum_3 = 0;         int i = 1;         int j = 1;         for (; i <= n; ++i) {             j = 1;             for (; j <= n; ++j) {                 sum_3 = sum_3 + i * j;             }         }         return sum_1 + sum_2 + sum_3;     }

但是如果是下面的代码，此时的时间复杂度就是O(m+n)了

就比如下面的代码，因为蓝色代码的时间复杂度是O(m)，然后红色代码的时间复杂度是O(n)，所以此时下面的cal的时间复杂度就是O(m+n)

 

int cal(int m, int n) {         int sum_1 = 0;         int i = 1;         for (; i < m; ++i) {             sum_1 = sum_1 + i;         }         int sum_2 = 0;         int j = 1;         for (; j < n; ++j) {             sum_2 = sum_2 + j;         }         return sum_1 + sum_2;     }

嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

 

比如下面的代码，因为在蓝色代码里面调用了另外一个方法，所以下的cal()方法的时间复杂度就是蓝O(n)*O(n)=O(n*n)

void cal(int n) {         int ret = 0;         int i = 1;         for (; i < n; ++i) {             ret = ret + f(i);         }     }     int f(int n) {         int sum = 0;         int i = 1;         for (; i < n; ++i) {             sum = sum + i;         }         return sum;     }

常见的时间复杂度

常见的时间复杂度如下所示

 

这里讲一下O(logn)和O(nlogn)这个时间复杂度的来历

首先看下面代码的时间复杂度，根据我们前面讲的复杂度分析方法，第三行代码是循环执行次数最多的。所以，我们只要能计算出这行代码被执行了多少次，就能知道整段代码的时间复杂度。

从代码中可以看出，变量i的值从1开始取，每循环一次就乘以2。当大于n时，循环结束。还记得我们高中学过的等比数列吗？实际上，变量i的取值就是一个等比数列。如果我把它一个一个列出来，就应该是这个样子的：

所以，我们只要知道x值是多少，就知道这行代码执行的次数了。通过2x=n求解x这个问题我们想高中应该就学过了，我就不多说了。x=log2n，所以，这段代码的时间复杂度就是O(log2n)。

 

int i = 1;         int n;         while(i<=n){             i = i * 3;         }

 

 

然后在看下面的代码，根据上面的代码，可以算出来此时的下面的代码的时间复杂度就是O(log3n)，但是不管是以2为底、以3为底，还是以10为底，我们可以把所有对数阶的时间复杂度都记为O(logn)。因为对数之间是可以互相转换的，log3n就等于log32 * log2n，所以O(log3n) = O(C * log2n)，其中C=log32是一个常量。基于我们前面的一个理论：在采用

大O标记复杂度的时候，可以忽略系数，即O(Cf(n)) = O(f(n))。所以，O(log2n) 就等于O(log3n)。因此，在对数阶时间复杂度的表示方法里，我们忽略对数的“底”，统一表示为O(logn)，这就是O(logn)的来历。

i=1;  while (i <= n) {  i = i * 3;  }

 

然后在根据上面的嵌套代码的规则，下面的代码的时间复杂度就是O(nlogn)

        

void cal(int m, int n) {         int j = 0;         for (int i = 0; i < n; i++) {             while (j < m) {                 j = j * 3;             }         }     }

 

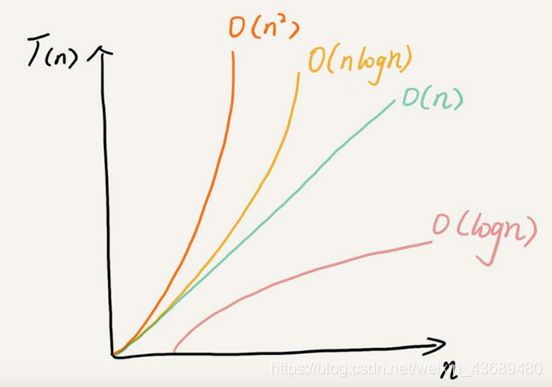
常见的时间复杂度在xy坐标里面的展示

 

时间复杂度的最好情况时间复杂度，最坏情况时间复杂度，平均情况时间复杂度

这是什么东西呢，就比如我们要在一个数组里面查询一个数据，在下面的代码里面，因为，要查找的变量x可能出现在数组的任意位置。如果数组中第一个元素正好是要查找的变量x，那就不需要继续遍历剩下的n-1个数据了，那时间复杂度就是O(1)。但如果数组中不存在变量x，那我们就需要把整个数组都遍历一遍，时间复杂度就成了O(n)。

 

在这个情况里面，最好情况时间复杂度就是O(1)，然后最坏的情况的时间复杂度就是O(n)，

// n表示数组array的长度,x表示要查询的值     int find(int[] array, int n, int x) {         int i = 0;         int pos = -1;         for (; i < n; ++i) {             if (array[i] == x) {                 pos = i;             }         }         return pos;     }

然后就是平均情况的时间复杂度，要查找的变量x在数组中的位置，有n+1种情况：在数组的0～n-1位置中和不在数组中。我们把每种情况下，查找需要遍历的元素个数累加起来(如果是在索引是0的位置找到了，那么就是就是查询了1次，然后如果在数组的索引是1的地方找到了，那么就是查询了2次。。。，如果是在n-1索引位置查询到了，那么就是n次，如果没有查询到，那么也是n次)，然后再除以n+1，就可以得到需要遍历的元素个数的平均值，即：

 

 

我们知道，时间复杂度的大O标记法中，可以省略掉系数、低阶、常量，所以，咱们把刚刚这个公式简化之后，得到的平均时间复杂度就是O(n)。

这个结论虽然是正确的，但是计算过程稍微有点儿问题。究竟是什么问题呢？我们刚讲的这n+1种情况，出现的概率并不是一样的。我带你具体分析一下。（这里要稍微用到一点儿概率论的知识，我们一般情况能理解到这里就可以了，下面的是想在深入的了解）

我们知道，要查找的变量x，要么在数组里，要么就不在数组里。这两种情况对应的概率统计起来很麻烦，为了方便你理解，我们假设在数组中与不在数组中的概率都为1/2。另外，要查找的数据出现在0～n-1这n个位置的概率也是一样的，为1/n。所以，根据概率乘法法则，要查找的数据出现在0～n-1中任意位置的概率就是1/(2n)。

因此，前面的推导过程中存在的最大问题就是，没有将各种情况发生的概率考虑进去。如果我们把每种情况发生的概率也考虑进去，那平均时间复杂度的计算过程就变成了这样：

这个值就是概率论中的加权平均值，也叫作期望值，所以平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。

引入概率之后，前面那段代码的加权平均值为(3n+1)/4。用大O表示法来表示，去掉系数和常量，这段代码的加权平均时间复杂度仍然是O(n)。

 

空间复杂度

 

空间复杂度全称就是渐进空间复杂度，表示算法的存储空间与数据规模之间的增长关系。

我还是拿具体的例子来给你说明

public static void cc(int n){         int j=n;         int[] a = new int[n];         for (int i=0; i             a[i] = i * i;         }     }

 

上面的蓝色代码我们申请了一个空间存储变量j，但是它是常量阶的，跟数据规模n没有关系，所以我们可以忽略。红色代码申请了一个大小为n的int类型数组，除此之外，剩下的代码都没有占用更多的空间，所以整段代码的空间复杂度就是O(n)。

我们常见的空间复杂度就是O(1)、O(n)、O(n2 )，像O(logn)、O(nlogn)这样的对数阶复杂度平时都用不到。

 

感觉极客时间大佬

能看到这里的同学，就帮忙右上角点个赞吧，Thanks♪(･ω･)ﾉ