数学分析 - 定积分（待修改）

简介：不定积分是求导的逆运算，定积分是某种特殊和式的极限

---

定积分的概念

|| 由例子引出定积分：曲边梯形的面积
在区间[a, b]中，取n-1个分点将区间分为n个小区间[x_i, x_i+1], i=1,2,…n，在每个小区间内都任取一点ξ_i 。将整个大曲边梯形划分为多个以f（ξ）为高，[x_i, x_i+1]为底的小矩形，用这些小矩形的面积之和将与某一常数无限接近，近似代替大曲边梯形的面积，即：

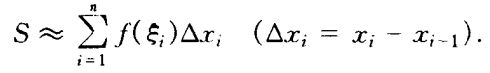
|| 以上的问题归结的思想方法总结为：“分割”，“近似求和”，”取极限“ ------最终归结为以一个特殊和式的逼近目标

|| 定义一：分割与模的定义
设闭区间[a, b]内有n-1个点（a=x₀12<…< x_n-1n=b）,它们将[a, b]分为n个小区间Δ_i = [x_i，x_i+1]，这些分点或闭子区间都对原区间构成了分割，记为： T={x₀,x₁,…,x_n}或{Δ₁,Δ₂,…,Δ_n}。小区间Δ_i的长度为Δx_i = x_i+1 - x_i，称作分割的模，记为： ||T||=max{Δx_i}
(分割的模即描述了分割的细密程度)

|| 定义二：积分和(黎曼和)的定义
设f是定义在[a, b]上的一个函数，对于区间[a, b]的一个分割T = {Δ₁,Δ₂,…,Δ_n},任取点ξ_i∈Δ_i ,i = 1,2,…n，并作和式：（下图），此和式为为函数f在[a, b]上的一个积分和，也称黎曼和

|| 定义三：定积分的定义
设函数f是定义在[a, b]上的一个函数，j是一个实数。若对于任给的正数ε，总存在某一个正数δ，使得对[a, b]的任意分割T，以及其上任意选取的的点集{ξ_i}，只要有|| T || < δ，就有：（下图），则称函数f在[a, b]上可积或黎曼可积，数 j记为 f 在[a, b]上的定积分或黎曼积分，记作：j=∫^b_a f(x)dx

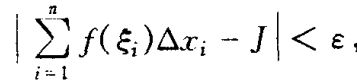
|| 有关定积分概念的补充叙述
注释1：从定义看,定积分其实就是一个特殊和式（积分和）的极限，因此可以写成这种形式:( 下图）

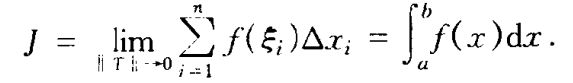
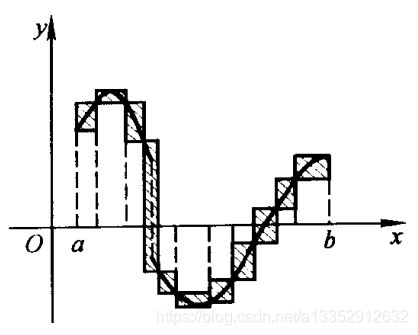
注释2：定积分的几何意义，可以看作正面积(y轴以上)和负面积(y轴以下)之和

注释3：一般来说b>a,当b=a时，定积分为0，当bb_af(x)dx = -∫^a_bf(x)dx

---

牛顿—莱布尼茨公式

简介：牛顿—莱布尼茨公式不仅提供了定积分计算的有效方法，并且在理论上把定积分和不定积分练习了起来。

|| 定理1：牛顿—莱布尼茨公式
若函数 f在区间[a, b]上连续, 则 f在[a, b]上可积，且定积分满足牛顿—莱布尼茨公式：

---

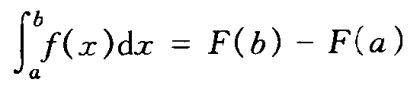
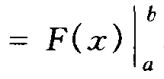
可积条件

由于直接通过定义来判断可积性十分困难，我们研究其他的判断可积性的条件，来证明除更多的定理和性质

|| 定理2：可积的必要条件
若函数 f 在[a, b]上可积，则f在[a, b ]上必定有界

|| 达布和的定义：
设 T 为 f 对于[a, b]的任一分割，其每个△_i存在上确界M和下确界m，则所有区间上确界和下确界的和称为f 关于 T的达布上和S（T）与达布下和：s（T）

|| 定理3：可积的充要条件（可积准则）
任给正数ε，总存在一个分割T，使得达布上和与达布下和的差小于ε（S(T) - s(T) < ε）

|| 定理3的另一种形式：设每一个△_i的上确界M和下确界m之差为ω（振幅），若每个子区间的中的振幅之和小于ε

|| 可积准则的几何意义：图中包围曲线的小正方形面积之和可以达到任意小

|| 定理4：若 f为[a, b]上的连续函数，则 f 在[a, b]上可积

|| 定理5：若 f是[a, b]上只有有限个间断点的有界函数，则 f在[a, b]上可积

|| 定理6：若 f是[a, b]上的单调函数，则 f在[a， b]上可积

---

定积分的性质

|| 性质1：倍乘运算
若 f在[a, b]上可积，k为常数，则kf在[a, b]上也可积，且 ∫^b_a f(x)dx = k ∫^b_a f(x)dx

|| 性质2：加减运算
若 f，g在[a, b]上可积，则 f ± g 在[a, b]上也可积，且 ∫^b_a [f(x) ± g(x)]dx = ∫^b_a f(x)dx ± ∫^b_ag(x)dx

|| 性质3：乘法运算
若 f，g在[a, b]上可积，则 f * g 在[a, b]上也可积，但是注意一般来说 ∫^b_a [f(x)* g(x)]dx !=∫^b_a f(x)dx * ∫^b_ag(x)dx （结果由推广的积分第一中值定理决定）

|| 性质4：可积的充要条件 (又称为积分区间的可加性)
f 在[a, b]可积的充要条件：任给c∈（a，b），f在[a, c]于[c, a]上都可积，且 ∫^b_a [f(x)]dx = ∫^c_a f(x)dx + ∫^b_c f(x)dx
（注意：针对分段函数的定积分求解）

|| 性质5：
若f 在[a, b]上可积，f（x）≥ 0，x∈[a, b]，则∫^b_a ≥ 0

|| 性质5的推论：积分不等式性
若 f，g在[a, b]上可积，且f（x）≥g（x），则 ∫^b_a f(x)dx ≥ ∫^b_a g(x)dx

|| 性质6：绝对值函数的可积性
若f 在[a, b]上可积，则 | f | 在[a, b]也可积，且 ∫^b_a | f(x) | dx= | ∫^b_a f(x)dx |
（注意：不可以反过来）

积分中值定理

|| 定理7：积分第一中值定理
若 f在[a, b]上连续，则至少存在一点ξ∈[a, b]，使得 ∫^b_a f(x)dx = f（ξ）(b - a)

|| 积分第一中值定理的几何意义
区间的长度 × 区间内某一函数值
（注意： f（ξ）= 1/(b-a) ∫^b_a f(x)dx 可以理解为区间所有函数值的平均值 ）

|| 定理8：推广的积分第一中值定理
若 f，g 在[a, b]上连续，且g（x）在[a, b]上不变号，则至少存在一点ξ∈[a, b]，使得 ∫^b_a [f(x)* g(x)]dx =f(ξ) * ∫^b_ag(x)dx

---

微积分学的基本定理

原函数存在定理（定理10）：在定积分形式下证明连续函数必定存在原函数
因为它沟通了导数与和定积分这两个表面上不相干的概念的内在联系，故被誉为微积分学的基本定理

|| 变限积分的的定义：（是一个函数）
以积分上限为自变量的函数 称为变上限的定积分：Φ（x） = ∫^x_a f(t)dt ，x∈[a, b]
以积分下限为自变量的函数 称为变下限的定积分：Ψ（x） = ∫^b_x f(t)dt ，x∈[a, b]
（注意：由于 ∫^b_x = - ∫^x_b，以下只讨论变上限积分）

|| 定理9：
若 f在[a, b]上可积，则函数 Φ在[a, b]上连续

|| 定理10：原函数存在定理
若 f在[a, b]上连续，则函数 Φ在[a, b]上可导，且：

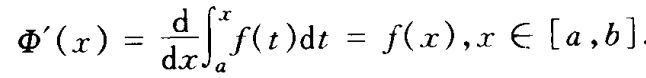
（注意：即连续函数必有原函数—变限积分）

|| 定理11：积分第二中值定理
设 f在[a, b]上可积：
1，若函数g在[a, b]上单调递减，且g( x )≥0，则存在ξ∈[a, b]，使得：

2，若函数g在[a, b]上单调递增，且g( x )≥0，则存在η∈[a, b]，使得：

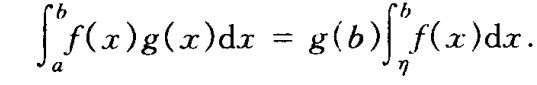
|| 积分第二中值定理的推论
设 f 在区间[a ,b]上可积，而g为单调函数，则存在ξ∈[a, b]，使得：

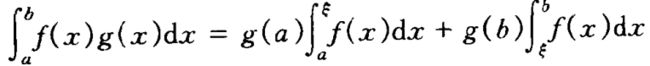
换元积分法和分部积分法
_{我们将把不定积分的两种积分法移植到定积分的运算中来}

|| 定理12：定积分换元积分法
若函数 f在[a，b]上连续，函数g在[α，β]上连续可微，且满足：g（α）= a，g（β）= b：
则有定积分换元积分公式：

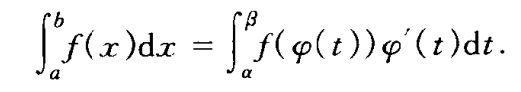
|| 定理13：定积分分部积分法
若函数 u，v在[a，b]上连续可微，则有定积分分部积分公式：

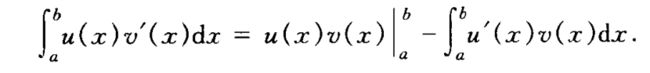
|| 两种泰勒公式余项：积分式余项，柯西式余项

---

可积性理论的补述
赶考试了，日后再补充…