CasRel：A Novel Cascade Binary Tagging Framework for Relational Triple Extraction 论文解读

A Novel Cascade Binary Tagging Framework for Relational Triple Extraction

论文：1909.03227.pdf (arxiv.org)

代码：github.com

期刊/会议：ACL 2020

摘要

从非结构化文本中抽取关系三元组对于大规模知识图构建至关重要。然而，现有的工作很少能解决重叠三元组问题，即同一句子中的多个关系三元组共享相同的实体。在这项工作中，我们引入了一个新的视角来重新审视关系三重抽取任务，并提出了一种新的级联二元标记框架（CASREL），该框架源自一个原则性问题公式。我们的新框架将关系建模为将句子中的subject映射到object的函数，而不是像以前的作品那样将关系视为离散标签，这自然会处理重叠问题。实验表明，即使其编码器模块使用随机初始化的BERT编码器，CASREL框架已经优于现有技术的方法，显示了新标记框架的效果。当采用预训练的BERT编码器时，它的性能进一步提高，在两个公共数据集NYT和WebNLG上，F1得分分别以17.5和30.2的绝对增益超过最强基线。对重叠三元组的不同场景的深入分析表明，该方法在所有这些场景中提供了一致的性能增益。

1、简介

关系三元组抽取的早期工作采用流水线方法（Zelenko等人，2003年；Zhou等人，2005年；Chan和Roth，2011年）。它首先识别句子中的所有实体，然后对每个实体对执行关系分类。由于早期阶段中的错误不能在后期阶段中被纠正，因此这种方法倾向于遭受错误传播问题。为了解决这个问题，随后的工作提出了实体和关系的联合学习，其中包括基于特征的模型（Yu和Lam，2010；Li和Ji，2014；Miwa和Sasaki，2014；Ren等人，2017），以及最近的基于神经网络的模型（Gupta等人，2016；Katiyar和Cardie，2017；Zheng等人，2014；Zeng等人，2018；Fu等人，2019）。通过用学习表示代替人工构建的特征，神经网络模型在三元组抽取任务中取得了相当大的成功。

然而，大多数现有方法不能有效地处理句子包含多个相互重叠的关系三元组的场景。图1说明了这些场景，其中三元组在一个句子中共享一个或两个实体。这种重叠的三元组问题直接挑战了传统的序列标记方案，该方案假设每个token只带有一个标签（Zheng等人，2017）。这也给关系分类方法带来了很大的困难，其中假设实体对最多持有一个关系（Miwa和Bansal，2016）。Zeng等人（2018）是最早考虑关系三元组抽取中重叠三元组问题的人之一。他们介绍了不同重叠模式的类别，如图1所示，并提出了一个具有复制机制的序列到序列（Seq2Seq）模型来抽取三元组。基于Seq2Seq模型，他们进一步研究了抽取顺序的影响（Zeng等人，2019），并通过强化学习获得了显著的改进。Fu等人（2019）还通过使用基于图卷积网络（GCN）的模型将文本建模为关系图，研究了重叠三元组问题。

尽管他们取得了成功，但以前关于抽取重叠三元组的工作仍有很多不足之处。具体来说，它们都将关系视为要分配给实体对的离散标签。这个公式使得关系分类成为一个困难的机器学习问题。首先，类别分布高度不平衡。在所有抽取的实体对中，大多数都没有形成有效的关系，产生了太多负样本。第二，当同一实体参与多个有效关系（重叠的三元组）时，分类器可能会被混淆。如果没有足够的训练实例，分类器很难判断实体参与了哪个关系。因此，抽取的三元组通常是不完整和不准确的。

在这项工作中，我们从三重层次的关系三重抽取权的原则公式开始。这产生了一个通用的算法框架，通过设计来处理重叠的三重问题。该框架的核心是一个全新的视角，即我们可以将关系建模为将subject映射到object的函数，而不是将关系视为实体对上的离散标签。更准确地说，我们学习关系特定标签$f_r(s)\to o$，代替学习关系分类器$f(s,o)\to r$， 其中每一个识别特定关系下给定subject的可能object；或不返回object，表示给定的subject和object不存在三元组。在这个框架下，三元组抽取是一个两步过程：首先我们识别句子中所有可能的subject；然后，对于每个subject，我们应用特定于关系的标记符来同时识别所有可能的关系和对应的object。

我们在端到端级联二元标记框架CASREL中实现了上述思想。它由基于BERT的编码器模块、subject标记模块和特定关系object标记模块组成。经验实验表明，即使在BERT编码器未经预训练的情况下，所提出的框架仍以较大幅度优于SOTA方法，表明了新框架本身的优越性。在采用预训练的BERT编码器后，该框架获得了更大的性能增益，表明了丰富的先验知识在三元组抽取任务中的重要性。

这项工作有以下主要贡献：

1. 我们引入了一个新的视角来重新审视关系三元组抽取任务，并提出了一个原则性的问题公式，这意味着一个通过设计解决重叠三元组问题的通用算法框架。
2. 我们将上述框架实例化为Transformer编码器之上的一个新的级联二元标记模型。这允许该模型将新颖标记框架的功能与预训练的大规模语言模型中的先验知识相结合。
3. 在两个公共数据集上的广泛实验表明，所提出的框架显著优于最先进的方法，在两个数据集上分别获得17.5和30.2的F1分数绝对增益。详细分析表明，我们的模型在所有场景中都得到了一致的改进。

2、相关工作

从非结构化自然语言文本中抽取关系三元组是信息抽取（IE）中一项研究得很好的任务。这也是构建大规模知识图（KG）的重要步骤，如DBpedia（Auer等人，2007）、Freebase（Bollacker等人，2008）和knowledge V ault（Dong等人，2014）。

早期的工作（Mintz等人，2009年；Gormley等人，2015年）以流水线方式解决了这项任务。他们在两个单独的步骤中抽取关系三元组：1）首先对输入句子运行命名实体识别（NER）以识别所有实体，2）然后对抽取的实体对运行关系分类（RC）。流水线方法通常存在误差传播问题，并且忽略了两个步骤之间的相关性。为了缓解这些问题，已经提出了许多旨在共同学习实体和关系的联合模型。传统的联合模型（Yu和Lam，2010；Li和Ji，2014；Miwa和Sasaki，2014；Ren等人，2017）是基于特征的，严重依赖特征工程，需要大量的人工工作。为了减少人工工作，最近的研究已经研究了基于神经网络的方法，这些方法可以提供最先进的性能。然而，大多数现有的神经模型（如Miwa和Bansal，2016）仅通过参数共享而不是联合解码来实现实体和关系的联合学习。为了获得关系三元组，他们仍然必须将检测到的实体对流水线到关系分类器，以识别实体的关系。分离的解码设置导致实体和关系的分离的训练目标，这带来了无法充分利用预测的实体和关系之间的三级依赖性的缺点。与这些工作不同，Zheng等人（2017）通过引入统一的标记方案来实现联合解码，并将关系三元组抽取任务转换为端到端序列标记问题，而无需NER或RC。由于实体和关系的信息被集成到统一的标记方案中，因此所提出的方法可以在三元组水平上将关系三元组作为一个整体直接建模。

尽管联合模型（有或没有联合解码）已经得到了很好的研究，但大多数以前的工作都忽略了重叠关系三元组的问题。Zeng等人（2018）引入了三种重叠的三元组模式，并试图通过具有复制机制的序列到序列模型来解决这个问题。最近，Fu等人（2019）也研究了该问题，并提出了一种基于图卷积网络（GCN）的方法。尽管最初取得了成功，但这两种方法仍然将关系视为实体对的离散标签，使得模型很难学习重叠的三元组。

我们的框架基于一个精心设计的训练目标，将关系三元组作为一个整体直接建模（Zheng等人，2017），即通过联合解码学习实体和关系。此外，我们将关系建模为将subject映射到object的函数，这使得它与以前的作品有着重大不同。

3、Casrel框架

关系三元组抽取的目标是识别句子中所有可能的（subject、relation、object）三元组，其中一些三元组可能与subject或object共享相同的实体。为了实现这一目标，我们直接对三元组水平进行建模，并在三元组水平上设计训练目标。这与之前的方法（Fu等人，2019）形成了对比，在这种方法中，单独为实体和关系定义了训练目标，而没有在三元组中明确建模其集成。

形式上，给定来自训练集$D$的标注语句$x_j$和$x_j$中的一组可能重叠的三元组$T_j=\{(s,r,o)\}$，我们的目标是最大化训练集$D$中的数据似然性：
∏ j = 1 ∣ D ∣ [ ∏ ( s , r , o ) ∈ T j p ( ( s , r , o ) ∣ x j ) ] \prod_{j=1}^{|D|} \left [ \prod_{(s,r,o) \in T_j}p((s,r,o)|x_j) \right] j=1∏∣D∣​ ​(s,r,o)∈Tj​∏​p((s,r,o)∣xj​) ​

= ∏ j = 1 ∣ D ∣ [ ∏ s ∈ T j p ( s ∣ x j ) ∏ ( r , o ) ∈ T j ∣ s p ( ( r , o ) ∣ s , x j ) ] =\prod_{j=1}^{|D|} \left [ \prod_{s \in T_j}p(s|x_j) \prod_{(r,o) \in T_j|s}p((r,o)|s,x_j) \right] =j=1∏∣D∣​ ​s∈Tj​∏​p(s∣xj​)(r,o)∈Tj​∣s∏​p((r,o)∣s,xj​) ​

= ∏ j = 1 ∣ D ∣ [ ∏ s ∈ T j p ( s ∣ x j ) ∏ r ∈ T j ∣ s p ( o ∣ s , x j ) ∏ r ∈ R ∖ T j ∣ s p r ( o ϕ ∣ s , x j ) ] =\prod_{j=1}^{|D|} \left [ \prod_{s \in T_j}p(s|x_j) \prod_{r \in T_j|s}p(o|s,x_j) \prod_{r \in R \setminus T_j|s}p_r(o_{\phi}|s,x_j) \right] =j=1∏∣D∣​ ​s∈Tj​∏​p(s∣xj​)r∈Tj​∣s∏​p(o∣s,xj​)r∈R∖Tj​∣s∏​pr​(oϕ​∣s,xj​) ​

这里我们稍微滥用了符号$T_j$。$s\in T_j$表示出现在$T_j$中的三元组中的subject。$T_j|s$是$T_j$中subject $s$引导的三元组集合。$(r,o)\in T_j|s$是由$T_j$中的subject $s$引导的三元组中的$(r,o)$对。$r$是所有可能关系的集合。$R\setminus T_j|s$表示除$T_j$中以$s$为首的关系之外的所有关系。$o_{\varnothing }$表示“空”对象（如下所述）。

等式（2）应用概率链式法则。等式（3）利用了一个关键事实，即对于给定的subject $s$，任何与$s$相关的关系（$T_j|s$中的关系）都会导致句子中相应的object，而所有其他关系都必然在句子中没有object，即“空”object。

这种方法提供了几个好处。首先，由于数据似然性从三元组开始，因此优化该似然性对应于直接优化三元组的最终评估标准。其次，通过不假设多个三元组如何共享句子中的实体，它通过设计处理了重叠的三元组问题。第三，等式（3）中的分解启发了一种新的三元组抽取标记方案：我们学习了一个识别句子中subject实体的subject标记器$p(s|x_j)$；对于每个关系$r$，我们学习一个object标记器$p_r(o|s,x_j)$，它识别给定subject的特定关系的object。通过这种方式，我们可以将每个关系建模为将subject映射到object的函数，而不是对（subject、object）对的关系进行分类。

事实上，这种新颖的标记方案允许我们一次抽取多个三元组：我们首先运行subject标记器来查找句子中所有可能的主题，然后针对找到的每个主题，应用特定关系的object标记器来找到所有相关的关系和对应的object。

上述通用框架中的关键组件，即subject标记器和特定关系的object标记器，可以以多种方式实例化。在本文中，我们将它们实例化为深度双向Transformer BERT之上的二元标记器（Devlin等人，2019）。我们将在下面描述其细节。

3.1 BERT编码器

编码器模块从句子$x_j$中抽取特征信息$x_j$，其将被馈送到后续的标记模块中。我们使用预训练的BERT模型（Devlin等人，2019）来编码上下文信息。

这里我们简要回顾了BERT，一种基于多层双向Transformer的语言表示模型。它旨在通过对每个单词的左右上下文进行联合调节来学习深度表达，最近在许多下游任务中被证明非常有效（Zhong等人，2019）。具体来说，它由$N$个相同的Transformer块组成。我们将Transformer块表示为$Trans(x)$，其中$x$表示输入向量。具体操作如下：
$$h_o=S{W}_s+W_p$$

$$h_{\alpha }=Trans(h_{\alpha -1}),\alpha \in [1,N]$$

其中$S$是输入句子中子词索引，是一个one-hot的矩阵，$W_s$是子词嵌入矩阵，$W_p$是位置嵌入矩阵，其中$p$表示输入序列中的位置索引，$h_{\alpha }$是隐藏状态向量，即，第$\alpha$层输入句子的上下文表示，$N$是Transformer块的数量。注意，在我们的工作中，输入是单个文本句子，而不是句子对，因此等式（4）中没有考虑原始BERT论文中描述的分段嵌入。有关Transformer结构的更全面描述，请参阅（Vaswani等人，2017）。

3.2 级联解码器

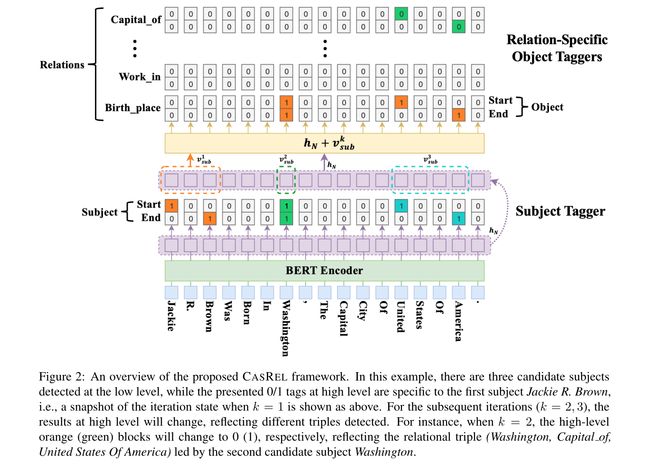
现在，我们描述受先前公式启发的新颖级联二元标记方案的实例化。基本思想是在两个级联步骤中抽取三元组。首先，我们从输入句子中检测subject。然后，对于每一个候选subject，我们检查所有可能的关系，看看一个关系是否可以将句子中的object与该subject相关联。对应于这两个步骤，级联解码器由两个模块组成，如图2所示：subject标记器；以及一组特定于关系的object标记器。

subject标记器：低级标记模块被设计为通过直接解码由$N$层BERT编码器产生的编码向量$h_N$来识别输入句子中的所有可能subject。更准确地说，它采用两个相同的二元分类器，通过为每个token分配指示当前token是否对应于subject的开始位置或结束位置的二元标记（0/1）来分别检测subject的开始和结束位置。subject标记器对每个token的详细操作如下：
$$p_i^{start-s}=\sigma (W_{start}{x}_i+b_{start})$$

$$p_i^{end-s}=\sigma (W_{end}{x}_i+b_{end})$$

$p_i^{start-s},p_i^{end-s}$分别表示将输入序列中的第$i$个token识别为subject的开始和结束位置的概率。如果概率超过某个阈值，则对应的token将被分配有标签1，否则将被分配标签0。$x_i$是输入序列中第$i$个标记的编码表示，即$x_i=h_N[i]$，其中$W(\cdot )$表示可训练权重，$b(\cdot )$是偏差，$\sigma$是sigmoid激活函数。

subject标记器优化了以下似然函数，以识别给定句子表示$x$的subject跨度：
$$p_{\theta }(s|x)=\prod _{t\in \{start-s,end-s\}}\prod _{i=1}^L(p_i^t{)}^{I\{y_i^t=1\}}(1-p_i^t{)}^{I\{y_i^t=0\}}$$
其中$L$是句子的长度。如果$z$为真，则$I\{z\}＝1$，否则为0。$y_i^{start-s}$是$x$中第$i$个token的subject开始位置的二元标记，$y_i^{end-s}$表示subject结束位置。参数$\theta ＝\{W_{start},b_{start},W_{end},b_{end}\}$。

对于多个subject检测，我们采用最近开始-结束对匹配原则，根据开始和结束位置标记器的结果来确定任何subject的跨度。例如，如图2所示，距离第一个开始标记“Jackie”最近的结束标记是“Brown”，因此第一个主题跨度的检测结果将是“Jackie R. Brown”。值得注意的是，为了将结束标记与给定的开始标记匹配，我们不考虑位置在给定token位置之前的标记。如果由于给定句子中任何实体跨度的自然连续性而正确检测到开始和结束位置，则这种匹配策略能够保持任何实体跨度。

特定关系的object标记器：高层标记模块同时识别object以及与在较低级别获得的subject相关的关系。如图2所示，它由一组特定关系的object标记器组成，其结构与底层模块中的subject标记器相同，适用于所有可能的关系。所有object标记器将同时识别每个检测subject的对应object。与直接解码编码向量$h_N$的subject标记器不同，关系特定object标记器也考虑了subject特征。关系特定object标记器对每个token的详细操作如下：
$$p_i^{start-o}=\sigma (W_{start}^r(x_i+v_{sub}^k)+b_{start}^r)$$

$$p_i^{end-o}=\sigma (W_{end}^r(x_i+v_{sub}^k)+b_{end}^r)$$

其中$p_i^{start-o}$和$p_i^{end-o}$表示将输入序列中的第$i$个token分别识别为object的开始和结束位置的概率，$v_{sub}^k$表示在低级别模块中检测到的第$k$个subject的编码表示向量。

对于每个subject，我们对其重复应用相同的解码过程。请注意，subject通常由多个标记组成，为了使等式（9）和等式（10）中的$x_i$和$v_{sub}^k$相加成为可能，我们需要保持两个向量的维数一致。为此，我们将第$k$个subject的开始和结束标记之间的平均向量表示作为$v_{sub}^k$。

关系$r$的object标记器优化了以下似然函数，以识别给定句子表示$x$和subject $s$的object $o$的跨度：
$$p_{{\varphi }_r}(o|s,x)=\prod _{t\in \{start-o,end-o\}}\prod _{i=1}^L(p_i^t{)}^{I\{y_i^t=1\}}(1-p_i^t{)}^{I\{y_i^t=0\}}$$
其中，$y_i^{start-o}$是$x$中第$i$个token的object开始位置的二元标记，$y_i^{end-o}$是第$i$个token的object结束位置的标记。对于“空”对象$o_{\varnothing }$，标记$y_i^{{start-o}_{\varnothing }}=y_i^{{end-o}_{\varnothing }}=0$表示所有$i$。参数${\varphi }_r=\{W_{start}^r,b_{start}^r,W_{end}^r,b_{end}^r\}$。

注意，在高级标记模块中，关系也由object标记器的输出决定。例如，检测到的subject“Jackie R. Brown”和候选object“Washington”。因此，关系“Work in”的object标记器不会识别“Washington”的跨度，即开始和结束位置的输出都为零，如图2所示。相反，“Birth_place”在“Jackie R. Brown”和“Washington”之间存在关系，因此相应的object标记器输出候选对象“Washington”的跨度。在此设置中，高级模块能够同时识别与在低级模块中检测到的subject相关的关系和object。

3.3 Data Log-likelihood Objective

J ( Θ ) = ∑ j = 1 ∣ D ∣ [ ∑ s ∈ T j log ⁡ p θ ( s ∣ x j ) + ∑ r ∈ T j ∣ s log ⁡ p ϕ r ( o ∣ s , x j ) + ∑ r ∈ R ∖ T j ∣ s log ⁡ p ϕ r ( o ϕ ∣ s , x j ) ] J(\Theta)=\sum_{j=1}^{|D|} \left[\sum_{s \in T_j} \log p_{\theta}(s|x_j)+\sum_{r \in T_j|s} \log p_{\phi_r}(o|s,x_j)+\sum_{r \in R \setminus T_j|s } \log p_{\phi_r}(o_{\phi}|s,x_j) \right] J(Θ)=j=1∑∣D∣​ ​s∈Tj​∑​logpθ​(s∣xj​)+r∈Tj​∣s∑​logpϕr​​(o∣s,xj​)+r∈R∖Tj​∣s∑​logpϕr​​(oϕ​∣s,xj​) ​

$\Theta =\{\theta ,\{{\varphi }_r{\}}_{r\in R}\}$，$p_{\theta }(s|x)$在公式8中被定义，$p_{{\varphi }_r}(o|s,x)$在公式11中被定义，我们最大化$J(\Theta )$作为训练目标。

4、实验

4.1 实验设置

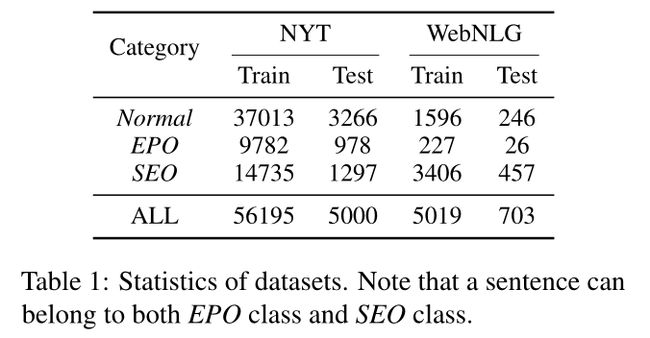
数据集和评估指标：NYT、WebNLG；Precision、Recall、F1-score。

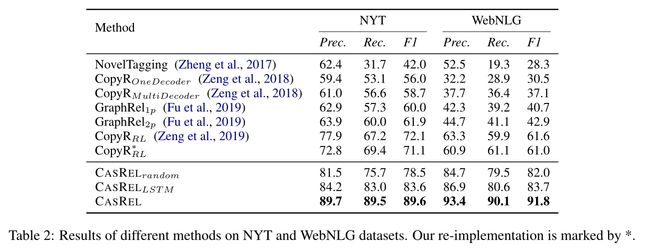
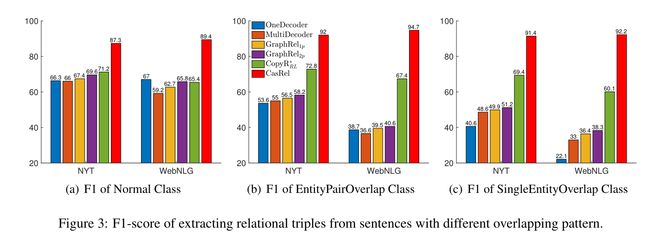
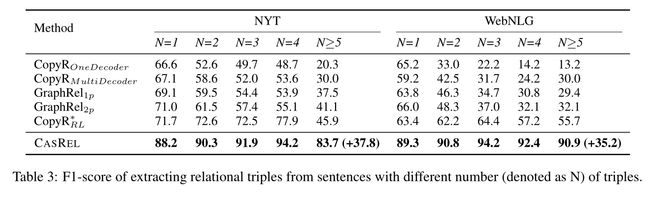
4.2 实验结果

5、总结

在本文中，我们介绍了一种新的级联二元标记框架（CASREL），该框架源自关系三元组抽取的原则问题公式。我们没有将关系建模为实体对的离散标签，而是将关系建模成将subject映射到object的函数，这为重新访问关系三重抽取任务提供了一个新的视角。因此，我们的模型可以同时从句子中抽取多个关系三元组，而不会出现重叠问题。我们在两个广泛使用的数据集上进行了广泛的实验，以验证所提出的CASREL框架的有效性。实验结果表明，我们的模型在不同的场景下，尤其是在抽取重叠的关系三元组方面，显著优于当前状态基线。

最近工作

自然语言处理和计算机视觉相关论文总结