LeetCode 313 周赛
文章目录
-
-
- 2427. 公因子的数目
- 2428. 沙漏的最大总和
- 2429. 最小 XOR
- 2430. 对字母串可执行的最大删除数
- 总结
-
2427. 公因子的数目
给你两个正整数 a 和 b ,返回 a 和 b 的 公 因子的数目。
如果 x 可以同时整除 a 和 b ,则认为 x 是 a 和 b 的一个 公因子 。
提示:1 <= a, b <= 1000
示例
输入:a = 12, b = 6
输出:4
解释:12 和 6 的公因子是 1、2、3、6 。
思路
一看数据范围是1000,直接暴力即可
// C++
class Solution {
public:
int commonFactors(int a, int b) {
int mi = min(a, b), ans = 0;
for (int i = 1; i <= mi; i++) {
if (a % i == 0 && b % i == 0) ans++;
}
return ans;
}
};
2428. 沙漏的最大总和
给你一个大小为 m x n 的整数矩阵 grid 。
按以下形式将矩阵的一部分定义为一个 沙漏 :
返回沙漏中元素的 最大 总和。
注意:沙漏无法旋转且必须整个包含在矩阵中。
示例
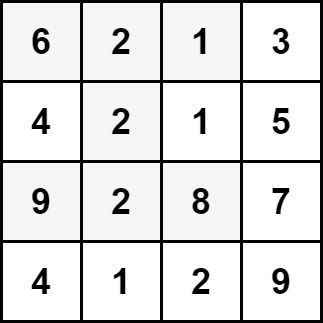
输入:grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]]
输出:30
解释:上图中的单元格表示元素总和最大的沙漏:6 + 2 + 1 + 2 + 9 + 2 + 8 = 30 。
思路
直接模拟一遍即可
// C++
class Solution {
public:
int maxSum(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
int ans = 0;
for (int i = 0; i <= n - 3; i++) {
for (int j = 0; j <= m - 3; j++) {
// [i, j] 是每个沙漏的左上角顶点
int t = 0;
for (int k = 0; k < 3; k++) t += grid[i][j + k];
t += grid[i + 1][j + 1];
for (int k = 0; k < 3; k++) t += grid[i + 2][j + k];
ans = max(ans, t);
}
}
return ans;
}
};
2429. 最小 XOR
给你两个正整数 num1 和 num2 ,找出满足下述条件的整数 x :
x的置位数和num2相同,且x XOR num1的值 最小
注意 XOR 是按位异或运算。
返回整数 x 。题目保证,对于生成的测试用例, x 是 唯一确定 的。
整数的 置位数 是其二进制表示中 1 的数目。
示例
输入:num1 = 3, num2 = 5
输出:3
解释:
num1 和 num2 的二进制表示分别是 0011 和 0101 。
整数 3 的置位数与 num2 相同,且 3 XOR 3 = 0 是最小的。
思路
先求得num2的二进制表示中1的数目cnt。然后构造x,x的二进制表示中,1的个数也要为cnt。
则我们需要,把cnt个1,放到x的某些二进制位上。
而由于要求x XOR num1的值最小。那么很明显的,先从高位到低位,看看num1的二进制表示中,哪些位为1,则把1放到x的对应位上。这样做异或可以抵消为0。如果已经构造到了x = num1,此时cnt个1还有剩余,则需要从低位往高位,把1放到那些为0的位置上去。
再贴一下y总的讲解
如果我们把1放到了num1中为1的那些位置上,做异或后,相当于是减去了一个数(这个位异或后抵消为0了),比如num1的第8位是1,如果我们在x中将第8位置为1,则异或的结果相当于在num1的基础上减去了一个2^7。
如果我们把1放到了num1中为0的那些位置上,做异或后,相当于是加上了一个数。
于是,我们需要将cnt个1放到对应的位置上,实际就是从若干个数中选择cnt个数,使得选出来的cnt个数的和最小。
假设num1的第1,3,5,8位是1。那么我们就需要从如下的数中选出cnt个(数据范围是10^9,则一共有30个二进制位)
... ,2^8,-2^7,2^6,2^5,-2^4,2^3,-2^2,2^1,-2^0
很明显的,要先选负数,且要从负的最多的数开始选。所以我们要从高位开始,选择num1中为1的那些位置。当num1中所有为1的位置都被选完了(负数都被选完了),此时cnt个数还有剩,那么只能选择正数,从最小的正数开始选,那么就是从低位开始,选择num1中为0的那些位置。
// C++
class Solution {
public:
int low_bit(int x) {
return x & -x;
}
int minimizeXor(int num1, int num2) {
// num2中1的个数, 这里统计1的个数, 可以用low_bit操作, 也可以直接遍历全部的位
int cnt = 0;
while (num2 > 0) {
num2 -= low_bit(num2);
cnt++;
}
// 10^9 < 2^30
// 一共最多30位
int x = 0;
// 先从高到低, 填充对应1的每一位
for (int i = 29; i >= 0; i--) {
// 剩余1的数量不够用了, 直接break
if (!cnt) break;
if (num1 >> i & 1) {
// 这个位置上num1为1, 则要将x这一位也置为1
x |= 1 << i;
cnt--; // 用掉了一个1
}
}
// 如果有剩余的cnt, 则要从低到高填充每个0的位置
if (cnt) {
for (int i = 0; i < 30; i++) {
if (!cnt) break; // 1的个数不够了, 直接break
if (!(x >> i & 1)) {
// 这个位置上num1为0
x |= 1 << i;
cnt--;
}
}
}
return x;
}
};
2430. 对字母串可执行的最大删除数
给你一个仅由小写英文字母组成的字符串 s 。在一步操作中,你可以:
- 删除 整个字符串
s,或者 - 对于满足
1 <= i <= s.length / 2的任意i,如果s中的 前i个字母和接下来的i个字母 相等 ,删除 前i个字母。
例如,如果 s = "ababc" ,那么在一步操作中,你可以删除 s 的前两个字母得到 "abc" ,因为 s 的前两个字母和接下来的两个字母都等于 "ab" 。
返回删除 s 所需的最大操作数。
提示:
1 <= s.length <= 4000s仅由小写英文字母组成
示例
输入:s = "aaabaab"
输出:4
解释:
- 删除第一个字母("a"),因为它和接下来的字母相等。现在,s = "aabaab"。
- 删除前 3 个字母("aab"),因为它们和接下来 3 个字母相等。现在,s = "aab"。
- 删除第一个字母("a"),因为它和接下来的字母相等。现在,s = "ab"。
- 删除全部字母。
一共用了 4 步操作,所以返回 4 。可以证明 4 是所需的最大操作数。
思路
动态规划+字符串哈希
自己重做虚拟竞赛时,第四题还是没做出来。
记录一下自己的思路:首先每次只能删除一个前缀。前缀能删到什么地方,取决于是否有两段重复的字符串。于是联想到kmp的next数组,尝试后发现并不适用。next数组求解出来的是最长公共前后缀,而不是紧挨着的两段重复字符串。看了眼数据范围,并结合这道题目,认为应该用动态规划来做,但是关于动态规划的状态表示,没有想明白。一开始想的是一维f[i],表示删掉前i个字符的最大次数。但是关于状态转移没想明白。这是因为我状态定义有问题。试想,如果求f[n],则考虑其如何转移,肯定是先删掉某个前缀[1, j],这记1次操作次数,然后再删除[j + 1, n],而后面这段区间,无法再用某个f来表示,这就是无法划分为子问题。
于是我又想到用二维,f[i, j]表示删除区间[i, j]所需要的最大次数。这又想偏了。
因为删除的过程中,始终只能删除某个前缀。而我们最终要求f[1, n],而f[1, n]一定是由删除某个前缀j转移过来的,删除前缀j记1次操作次数,则f[1, n] = 1 + f[j + 1, n]。可以看到f数组的第二维其实是一直不会变的,一直是n,所以用二维动规貌似没必要。
想到这里,其实已经比较接近正确思路了。但我卡着一直没想通。
其实,只要设f[i]表示,删除[i, n]的最大操作次数即可。
考虑其如何转移,f[i]要么是直接删除整个字符串,即此时f[i] = 1;要么是先删掉一部分前缀,假设删除的前缀为[i, j],再删[j + 1, n],删除前缀[i, j]记1次,则f[i] = 1 + f[j + 1]。
那么我们只要枚举一下所有可能的前缀,即可完成状态转移。那么如何快速判断一个前缀能否满足条件呢?这里要用到字符串哈希。
比如我们求解f[i]时,枚举所有可能的前缀,假设前缀长度为j
则我们需要判断一下区间[i, i + j - 1]与[i + j, i + j * 2 - 1]是否相等,这一步可以用字符串哈希将时间复杂度将为 O ( 1 ) O(1) O(1)。
而我们f[i]转移时依赖f[i + j],所以状态要从右往左计算。如此,能够在时间复杂度 O ( n 2 ) O(n^2) O(n2) 内求得答案。
C++:
// C++
typedef unsigned long long ULL;
class Solution {
public:
vector<ULL> p;
vector<ULL> h; // 字符串哈希
ULL get(int l, int r) {
return h[r] - h[l - 1] * p[r - l + 1];
}
int deleteString(string s) {
int n = s.size(), P = 131;
p.resize(n + 1), h.resize(n + 1);
// 预处理
p[0] = 1;
for (int i = 1; i <= n; i++) {
h[i] = h[i - 1] * P + s[i - 1];
p[i] = p[i - 1] * P;
}
vector<int> f(n + 1);
// 从右往左转移
for (int i = n; i >= 1; i--) {
f[i] = 1; // 删除[i, n] 的操作次数至少为1, 即删除整个字符串
// 枚举全部可能的前缀长度
for (int j = 1; i + j * 2 - 1 <= n; j++) {
// 判断2个区间的子串是否相等
// [i, i + j - 1]
// [i + j, i + j * 2 - 1];
if (get(i, i + j - 1) == get(i + j, i + j * 2 - 1)) {
// 两部分相同, 则可以转移, 删掉 [i, i + j - 1]
f[i] = max(f[i], f[i + j] + 1);
}
}
}
// [1, n]
return f[1];
}
};
Java:
// Java
class Solution {
long[] p;
long[] h;
private long get(int l, int r) {
return h[r] - h[l - 1] * p[r - l + 1];
}
public int deleteString(String s) {
int n = s.length(), P = 131;
h = new long[n + 1];
p = new long[n + 1];
p[0] = 1; //P^0 = 1
for (int i = 1; i <= n; i++) {
h[i] = h[i - 1] * P + s.charAt(i - 1) - 'a';
p[i] = p[i - 1] * P;
}
int[] f = new int[n + 1];
for (int i = n; i >= 1; i--) {
f[i] = 1;
for (int j = 1; i + j * 2 - 1 <= n; j++) {
if (get(i, i + j - 1) == get(i + j, i + j * 2 - 1)) {
f[i] = Math.max(f[i], f[i + j] + 1);
}
}
}
return f[1];
}
}
总结
T1,T2都是直接暴力模拟;T3是位运算+贪心;T4是动态规划+字符串哈希。
今天重做,只做出3道,还需再接再厉。