代码随想录算法训练营day58 | 单调栈 739. 每日温度 496.下一个更大元素 I
day58
-
-
- 739. 每日温度
-
- 1.单调栈里存放的元素是什么?
- 2.单调栈里元素是递增呢? 还是递减呢?
- 496.下一个更大元素 I
-
739. 每日温度
题目链接
解题思路: 单调栈的本质是空间换时间,因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素,优点是整个数组只需要遍历一次。
更直白来说,就是用一个栈来记录我们遍历过的元素,因为我们遍历数组的时候,我们不知道之前都遍历了哪些元素,以至于遍历一个元素找不到是不是之前遍历过一个更小的,所以我们需要用一个容器(这里用单调栈)来记录我们遍历过的元素。
在使用单调栈的时候首先要明确如下几点:
1.单调栈里存放的元素是什么?
单调栈里只需要存放元素的下标i就可以了,如果需要使用对应的元素,直接T[i]就可以获取。
2.单调栈里元素是递增呢? 还是递减呢?
注意以下顺序的描述为 从栈头到栈底的顺序
这里要使用递增循序(再强调一下是指从栈头到栈底的顺序),因为只有递增的时候,栈里要加入一个元素i的时候,才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是i。
即:如果求一个元素右边第一个更大元素,单调栈就是递增的,如果求一个元素右边第一个更小元素,单调栈就是递减的。
文字描述理解起来有点费劲,接下来我画了一系列的图,来讲解单调栈的工作过程,大家再去思考,本题为什么是递增栈。
使用单调栈主要有三个判断条件。
- 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
把这三种情况分析清楚了,也就理解透彻了。
接下来我们用temperatures = [73, 74, 75, 71, 71, 72, 76, 73]为例来逐步分析,输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
首先先将第一个遍历元素加入单调栈
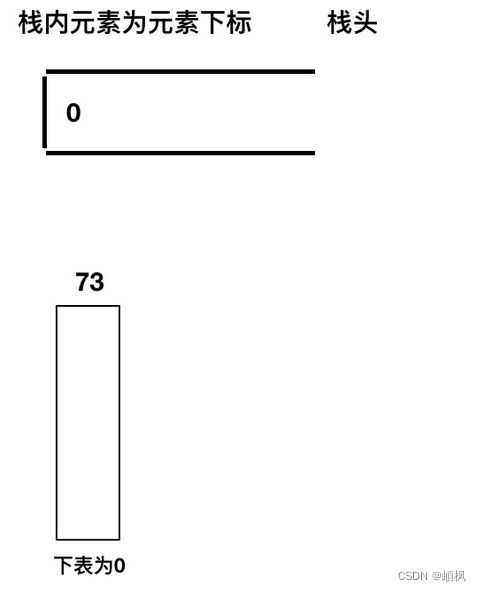
加入T[1] = 74,因为T[1] > T[0](当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况)。
我们要保持一个递增单调栈(从栈头到栈底),所以将T[0]弹出,T[1]加入,此时result数组可以记录了,result[0] = 1,即T[0]右面第一个比T[0]大的元素是T[1]。
 加入
加入T[2],同理,T[1]弹出
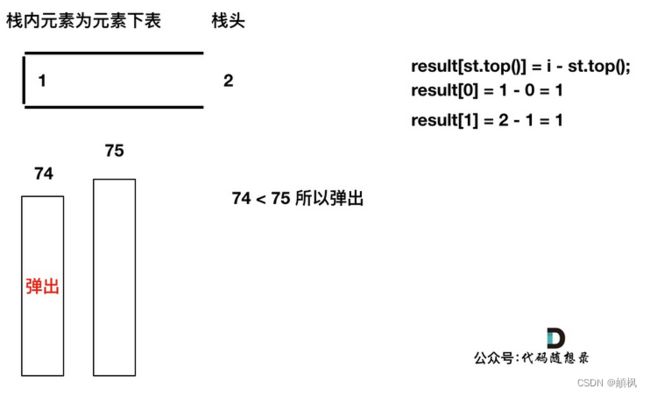 加入
加入T[3],T[3] < T[2] (当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况),加T[3]加入单调栈。
 加入
加入T[4],T[4] == T[3] (当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况),此时依然要加入栈,不用计算距离,因为我们要求的是右面第一个大于本元素的位置,而不是大于等于!
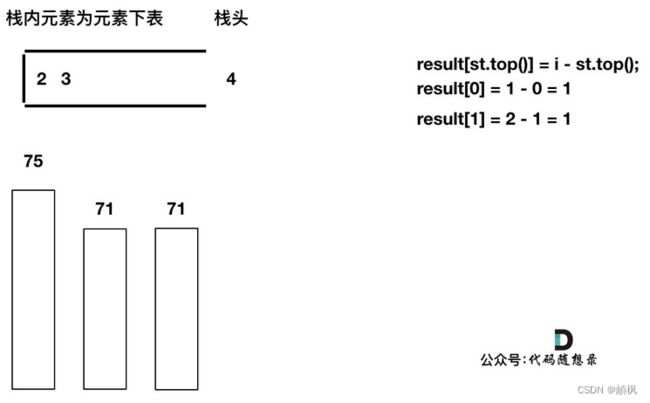 加入
加入T[5],T[5] > T[4] (当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况),将T[4]弹出,同时计算距离,更新result

T[4]弹出之后, T[5] > T[3] (当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况),将T[3]继续弹出,同时计算距离,更新result
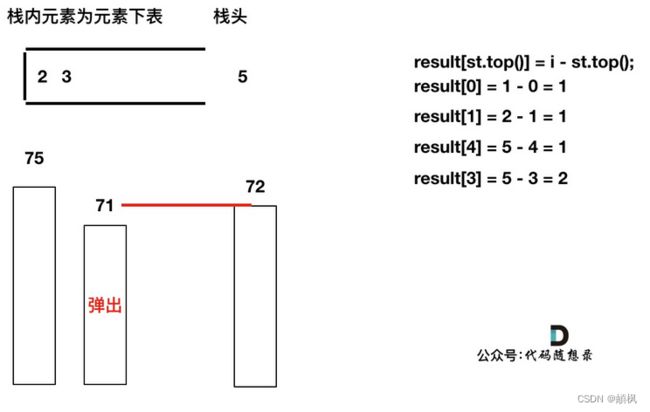 直到发现
直到发现T[5]小于T[st.top()],终止弹出,将T[5]加入单调栈
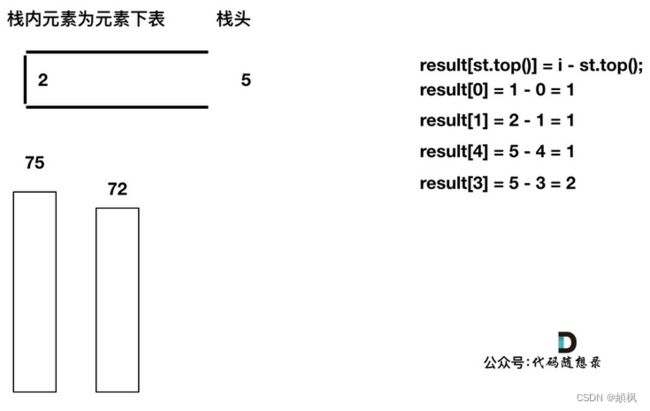 加入
加入T[6],同理,需要将栈里的T[5],T[2]弹出
 同理,继续弹出
同理,继续弹出
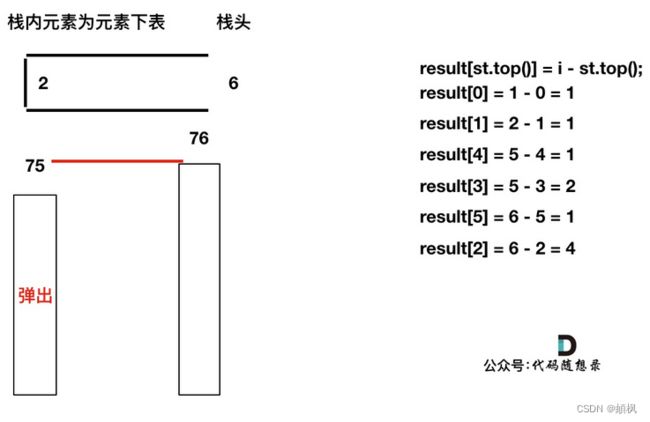
此时栈里只剩下了T[6]
 加入
加入T[7], T[7] < T[6] 直接入栈,这就是最后的情况,result数组也更新完了。
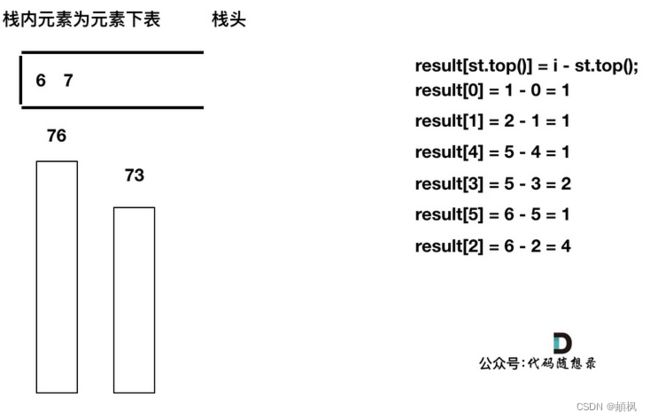 此时有同学可能就疑惑了,那
此时有同学可能就疑惑了,那result[6] , result[7]怎么没更新啊,元素也一直在栈里。
其实定义result数组的时候,就应该直接初始化为0,如果result没有更新,说明这个元素右面没有更大的了,也就是为0。
以上在图解的时候,已经把,这三种情况都做了详细的分析。
- 情况一:当前遍历的元素T[i]小于栈顶元素
T[st.top()]的情况 - 情况二:当前遍历的元素T[i]等于栈顶元素
T[st.top()]的情况 - 情况三:当前遍历的元素T[i]大于栈顶元素
T[st.top()]的情况
通过以上过程,大家可以自己再模拟一遍,就会发现:只有单调栈递增(从栈口到栈底顺序),就是求右边第一个比自己大的,单调栈递减的话,就是求右边第一个比自己小的。
C++代码如下:
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& T) {
// 递增栈
stack<int> st;
vector<int> result(T.size(), 0);
st.push(0);
for (int i = 1; i < T.size(); i++) {
if (T[i] < T[st.top()]) { // 情况一
st.push(i);
} else if (T[i] == T[st.top()]) { // 情况二
st.push(i);
} else {
while (!st.empty() && T[i] > T[st.top()]) { // 情况三
result[st.top()] = i - st.top();
st.pop();
}
st.push(i);
}
}
return result;
}
};
496.下一个更大元素 I
题目链接
解题思路:
本题则是说nums1 是 nums2 的子集,找nums1中的元素在nums2中下一个比当前元素大的元素。
看上去和上一题是一样的,但是这么绕了一下,其实还上升了一点难度。
需要对单调栈使用的更熟练一些,才能顺利的把本题写出来。
从题目示例中我们可以看出最后是要求nums1的每个元素在nums2中下一个比当前元素大的元素,那么就要定义一个和nums1一样大小的数组result来存放结果。
一些同学可能看到两个数组都已经懵了,不知道要定一个一个多大的result数组来存放结果了。
这么定义这个result数组初始化应该为多少呢?
题目说如果不存在对应位置就输出 -1 ,所以result数组如果某位置没有被赋值,那么就应该是是-1,所以就初始化为-1。
在遍历nums2的过程中,我们要判断nums2[i]是否在nums1中出现过,因为最后是要根据nums1元素的下标来更新result数组。
注意题目中说是两个没有重复元素 的数组 nums1 和 nums2。
没有重复元素,我们就可以用map来做映射了。根据数值快速找到下标,还可以判断nums2[i]是否在nums1中出现过。
C++中,当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的。我在关于哈希表,你该了解这些!
那么预处理代码如下:
unordered_map<int, int> umap; // key:下标元素,value:下标
for (int i = 0; i < nums1.size(); i++) {
umap[nums1[i]] = i;
}
使用单调栈,首先要想单调栈是从大到小还是从小到大。
本题和上一题一样的。
栈头到栈底的顺序,要从小到大,也就是保持栈里的元素为递增顺序。只要保持递增,才能找到右边第一个比自己大的元素。
可能这里有一些同学不理解,那么可以自己尝试一下用递减栈,能不能求出来。其实递减栈就是求右边第一个比自己小的元素了。
接下来就要分析如下三种情况,一定要分析清楚。
- 情况一:当前遍历的元素
T[i]小于栈顶元素T[st.top()]的情况
此时满足递增栈(栈头到栈底的顺序),所以直接入栈。
- 情况二:当前遍历的元素
T[i]等于栈顶元素T[st.top()]的情况
如果相等的话,依然直接入栈,因为我们要求的是右边第一个比自己大的元素,而不是大于等于!
- 情况三:当前遍历的元素
T[i]大于栈顶元素T[st.top()]的情况
此时如果入栈就不满足递增栈了,这也是找到右边第一个比自己大的元素的时候。
判断栈顶元素是否在nums1里出现过,(注意栈里的元素是nums2的元素),如果出现过,开始记录结果。
记录结果这块逻辑有一点小绕,要清楚,此时栈顶元素在nums2数组中右面第一个大的元素是nums2[i](即当前遍历元素)。
代码如下:
while (!st.empty() && nums2[i] > nums2[st.top()]) {
if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下标
result[index] = nums2[i];
}
st.pop();
}
st.push(i);
以上分析完毕,C++代码如下:
class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
stack<int> st;
vector<int> result(nums1.size(), -1);
if (nums1.size() == 0) return result;
unordered_map<int, int> umap; // key:下标元素,value:下标
for (int i = 0; i < nums1.size(); i++) {
umap[nums1[i]] = i;
}
st.push(0);
for (int i = 1; i < nums2.size(); i++) {
if (nums2[i] < nums2[st.top()]) { // 情况一
st.push(i);
} else if (nums2[i] == nums2[st.top()]) { // 情况二
st.push(i);
} else { // 情况三
while (!st.empty() && nums2[i] > nums2[st.top()]) {
if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下标
result[index] = nums2[i];
}
st.pop();
}
st.push(i);
}
}
return result;
}
};