Python解微分方程(验证数学建模第五版火箭发射模型)

目录

1.Python解微分方程数值解

2.验证火箭发射模型

---

1.Python解微分方程数值解

Python解微分方程要用到几个库：numpy, matplotlib.pyplot, scipy.integrate，没有的话就

pip install 相应的库就行，本次用的python为3.6.8

我们先来看一下简单的微分方程

 对于Python求解微分方程只需要跳相应的库即可

from typing import List

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint


# 一阶微分方程的例子
def diff_equation(y_list: List[float], x: float):
    y1, y2, y3 = y_list
    return np.array([y2 * y3, -y1 * y3, -0.51 * y1 * y2])  # 微分方程格式，左边一定是dy/dx,返回右边


x = np.linspace(0, 12, 100)  # 初始点是0,终点是12，其中有100个点
result = odeint(diff_equation, [0, 1, 1], x)  # 中间那个是y初值
plt.plot(x, result[:, 0], label='y1')  # result整个矩阵的第一列
plt.plot(x, result[:, 1], label='y2')
plt.plot(x, result[:, 2], label='y3')

plt.legend()
plt.grid()  # 网格
plt.show()  # 这是y=f(x)的图像

结果展示

2.验证火箭发射模型

掌握了解方程之后我们就可以来验证火箭发射模型了

高阶微分方程，我们可以化为微分方程组来解，在这里书上义给出微分方程组，但只给出了0~t1阶段即火箭燃料还有的阶段，t1~t2为燃料耗尽的时间阶段，其中r=18，t1~t2的微分方程组为 -g+(-k*x2*x2/m),这里的m是火箭净重量。

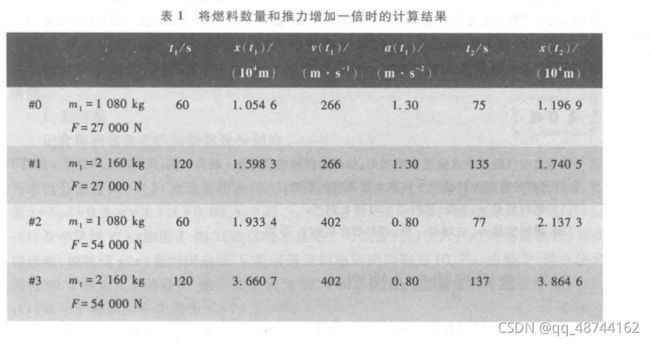
为了验证以下表格

代码如下 

from typing import List

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint


def get_acceleration(x: np.ndarray, result: np.ndarray, time: float, f: float, m: float, g: float,
                     k: float) -> np.ndarray:
    """
    获取火箭发射的加速度
    :param x: 距离数组
    :param result:
    :param time:  时间
    :param f: 外力
    :param m: 质量
    :param g :重力加速度
    :param k : 阻力系数
    :return: 加速度数组
    """
    temp = []
    # 重力加速度
    result = result[:, 1]
    for i in range(np.size(result)):
        if x[i] < time:
            temp.append(-g + (f - k * pow(result[i], 2)) / (m - x[i] * 18))
        else:
            temp.append(-g + (- k * pow(result[i], 2)) / 520)
    return np.array(temp)


def diff_equation1(x_list: List[float], x: float):
    x1, x2 = x_list

    temp = ((27000 - 0.3 * x2 * x2) / (1600 - x * 18)) if x <= 60 else -0.3 * x2 * x2 / 520
    return np.array([x2, -9.8 + temp])  # 微分方程格式，左边一定是dy/dx,返回右边


def diff_equation2(x_list: List[float], x: float):
    x1, x2 = x_list

    temp = ((27000 * 2 - 0.3 * x2 * x2) / (1600 - x * 18)) if x <= 60 else -0.3 * x2 * x2 / 520
    return np.array([x2, -9.8 + temp])  # 微分方程格式，左边一定是dy/dx,返回右边


def diff_equation3(x_list: List[float], x: float):
    x1, x2 = x_list

    temp = ((27000 - 0.3 * x2 * x2) / (2680 - x * 18)) if x <= 120 else -0.3 * x2 * x2 / 520
    return np.array([x2, -9.8 + temp])  # 微分方程格式，左边一定是dy/dx,返回右边


def diff_equation(x_list: List[float], x: float):
    x1, x2 = x_list

    temp = ((27000 * 2 - 0.3 * x2 * x2) / (2680 - x * 18)) if x <= 120 else -0.3 * x2 * x2 / 520
    return np.array([x2, -9.8 + temp])  # 微分方程格式，左边一定是dy/dx,返回右边


x = np.linspace(0, 140, 10000)  # 初始点是0
x1 = np.linspace(0, 80, 10000)
result = odeint(diff_equation, [0., 0.], x)  # 中间那个是y0初值，即x=0时y=1
result1 = odeint(diff_equation1, [0., 0.], x1)
result2 = odeint(diff_equation2, [0., 0.], x1)
result3 = odeint(diff_equation3, [0., 0.], x)

# 加速度
plt.plot(x, get_acceleration(x, result, 120, 27000 * 2, 2680, 9.8, 0.3), label='a3(t)')
plt.plot(x1, get_acceleration(x1, result2, 60, 27000 * 2, 1600, 9.8, 0.3), label='a2(t)')
plt.plot(x, get_acceleration(x, result3, 120, 27000, 2680, 9.8, 0.3), label='a1(t)')
plt.plot(x1, get_acceleration(x1, result1, 60, 27000, 1600, 9.8, 0.3), label='a0(t)')

# 路程
# plt.plot(x, result[:, 0], label='x3(t)')
# plt.plot(x1, result1[:, 0], label='x2(t)')
# plt.plot(x, result2[:, 0], label='x1(t)')
# plt.plot(x1, result3[:, 0], label='x0(t)')

# 速度
# plt.plot(x, result[:, 1], label='v3(t)')
# plt.plot(x1, result1[:, 1], label='v2(t)')
# plt.plot(x, result2[:, 1], label='v1(t)')
# plt.plot(x1, result3[:, 1], label='v0(t)')
# plt.xlim(left=0)
# plt.ylim(bottom=0)

plt.legend()
plt.grid()  # 网格
plt.show()  # 这是微分方程的图像

结果展示

x的关系图

 v的关系图

a的关系图

 闲着没事干写的，写的不是很好，有疑问可以发我邮箱[email protected]

感谢ssw小伙伴的指正！

妈妈，他们抛弃了我 像歌唱一样抛弃了我

妈妈，我是多么爱你 当你沉默的时候我爱你

只是那些猛烈的情绪

在睡不着的时候折磨着我

我那早已死去的父亲

在没有星星的夜晚看着你

妈妈，我会在夏天开放吗

像你曾经的容颜那样

妈妈，这种失落会持久吗

这个世界会好吗

忘记一些隐秘的委屈

在回头观望的时候迷失了自己

我的正在老去的身体

从某一天开始就在渐渐死去

妈妈我爱你

妈妈，我居然爱上了她

像歌唱一样就爱上了她

妈妈，当你又回首一切

这个世界会好吗

妈妈，我是多么恨你

当我歌唱的时候我恨你