《Python数据分析与挖掘实战》第13章——回归+DNN

本文是基于《Python数据分析与挖掘实战》的实战部分的第13章的数据——《财政收入影响因素分析及预测模型》做的分析。

旨在补充原文中的细节代码，并给出文中涉及到的内容的完整代码。

在作者所给代码的基础上增加的内容包括： 

1）探索了灰色预测的原理 

2）画出预测结果图

3）由于书中使用的是AdaptiveLasso，但是没有找到该函数，所以采用了其他变量选择模型

1 挖掘背景及目标

    根据1994-2013年相关财政数据 ，梳理影响地方财政收入的关键特征，对未来几年的财政数据进行预测。 

    实质：回归

2 数据探索

# 概括性分析描述性统计
r = [data.min(), data.max(), data.mean(), data.std()] #统计最小、最大、平均、标准差
r = pd.DataFrame(r, index= ['Min', 'Max', 'Mean', 'Std']).T #计算相关系数矩阵
result = np.round(r, 2) # 保留两位小数  （***）
# np.round(data.describe().T[['min', 'max', 'mean', 'std']],2) # 等价于上面数据探索
#保存的表名命名格式为“1_k此表功能名称”，是此小节生成的第1张表格，功能为summaryMeasure：概括性分析描述性统计
result.to_excel('1_1summaryMeasure.xlsx')
result

# 计算各个变量之间的皮尔森系数'pearson'/ 'kendall'/ 'spearman'
result1 = np.round(data.corr(method='pearson'), 2)
#保存的表名命名格式为“1_k此表功能名称”，是此小节生成的第2张表格，功能为relatedAnalysis：相关性分析
result1.to_csv("1_2relatedAnalysis.csv")
result1

2 数据预处理——数据规约

2.1 降维

from sklearn.linear_model import Lasso# AdaptiveLasso找不到
# LASSO回归的特点是在拟合广义线性模型的同时进行变量筛选和复杂度调整。 因此，不论目标因变量是连续的，还是二元或者多元离散的，
#都可以用LASSO回归建模然后预测。 这里的变量筛选是指不把所有的变量都放入模型中进行拟合，而是有选择的把变量放入模型从而得到更好的性能参数。
model = Lasso(alpha = 0.1)
model.fit(data.iloc[:,:13], data['y']) # data.iloc[:, 0:13]
print model.coef_ # 各个特征权重weight
print model.intercept_ # 输出偏置bias

输出结果：

[ -1.88512448e-04 -2.68436321e-01 4.45960813e-01 -3.24264041e-02
7.25657667e-02 4.52109484e-04 2.28596158e-01 -4.51460904e-02
-3.10503208e+00 6.19423002e-01 4.80398130e+00 -9.79664624e+01
-3.86933684e-02]
-2650.99589437

3 模型构建

由于有多个指标需要预测建模，但是各自又有雷同之处，所以，此处以“某市财政收入预测模型” 为例

3.1 灰色预测

此处利用灰色预测，预测出2014-2015年的各个变量的数据，为接下来建模准备

# 灰色预测：灰色预测是一种对含有不确定因素的系统进行预测的方法，灰色预测通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。
# 其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。
# 灰色理论建立的是生成数据模型，不是原始数据模型
# 数据生成方式：A：累加生成：通过数列间各时刻数据的依个累加得到新的数据与数列。累加前数列为原始数列，累加后为生成数列。B：累减生成 C：其他

# 优势：是处理小样本数据预测问题的有效工具

# 灰色预测函数
def GM11(x0): #自定义灰色预测函数  #该函数覆盖了导入的包的同名函数
    import numpy as np
    x1 = x0.cumsum() #1-AGO序列
    z1 = (x1[:len(x1)-1] + x1[1:])/2.0 #紧邻均值（MEAN）生成序列 # 由常微分方程可知，取前后两个时刻的值的平均值代替更为合理
    # x0[1] = -1/2.0*(x1[1] + x1[0])
    z1 = z1.reshape((len(z1),1))
    B = np.append(-z1, np.ones_like(z1), axis = 1) # (***)
    Yn = x0[1:].reshape((len(x0)-1, 1))
    [[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数
#     fkplusone = (x1[0]-b/a)*np.exp(-a*k)#时间响应方程 # 由于x0[0] = x1[0]
    f = lambda k: (x1[0]-b/a)*np.exp(-a*(k-1))-(x1[0]-b/a)*np.exp(-a*(k-2)) #还原值 
    delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)])) # 残差
    C = delta.std()/x0.std() # 后验比差值
    P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
    return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率

data.loc[2014] = None
data.loc[2015] = None
h = ['x1', 'x2', 'x3', 'x4', 'x5', 'x7']
P = []
C = []
for i in h:
    gm = GM11(data[i][range(1994, 2014)].as_matrix())
    f = gm[0] ##获得灰色预测函数
    P = gm[-1] # 获得小残差概率
    C = gm[-2] # 获得后验比差值
    data[i][2014] = f(len(data)-1)
    data[i][2015] = f(len(data))
    data[i] = data[i].round(2) # 保留2位小数
    if (C < 0.35 and P > 0.95): # 评测后验差判别
        print '对于模型%s，该模型精度为---好' % i
    elif (C < 0.5 and P > 0.8):
        print '对于模型%s，该模型精度为---合格' % i
    elif (C < 0.65 and P > 0.7):
        print '对于模型%s，该模型精度为---勉强合格' % i
    else:
        print '对于模型%s，该模型精度为---不合格' % i

输出结果为：

对于模型x1，该模型精度为---好
对于模型x2，该模型精度为---好
对于模型x3，该模型精度为---好
对于模型x4，该模型精度为---好
对于模型x5，该模型精度为---好
对于模型x7，该模型精度为---好

#保存的表名命名格式为“2_1_2_1k此表功能名称”，是此小节生成的第1张表格，功能为greyPredict：灰色预测
data[h+['y']].to_excel('2_1_2_1greyPredict.xlsx')

data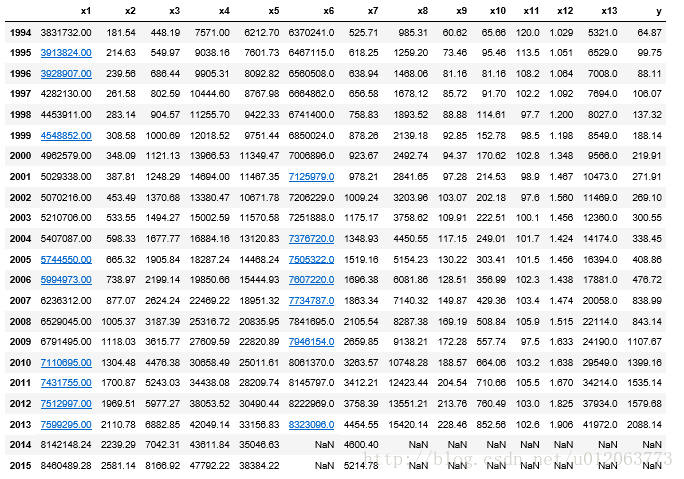

3.2 神经网络

inputfile1 = '2_2_2_1greyPredict.xlsx'
data = pd.read_excel(inputfile1)
data # 1994到2013年间的各个影响因素的数据
feature = ['x1', 'x3',  'x5'] # 特征所在列

# 准备模型数据
data_train = data.loc[range(1999,2014)].copy() # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train-data_mean)/data_std # 均值标准化
x_train = data_train[feature].as_matrix() # 特征数据
y_train = data_train['y'].as_matrix() # 标签数据

# 利用神经网络建模
from keras.models import Sequential
from keras.layers.core import Dense, Activation
import time 
start = time.clock()

#输入层为３个节点，隐藏层６个节点
model = Sequential() # 建立模型
model.add(Dense(output_dim =6, input_dim=3)) # 添加输入层、隐藏层节点
model.add(Activation('relu')) # 使用relu作为激活函数，可以大幅度提高准确率
model.add(Dense(units=1, input_dim=6)) # 添加输出层节点
model.compile(loss = 'mean_squared_error', optimizer = 'adam') # 编译模型
model.fit(x_train, y_train, nb_epoch = 3000, batch_size=16) #训练模型，学习一千次
end = time.clock()
usetime = end-start
print '训练该模型耗时'+ str(usetime) +'s!'
model.save_weights('2_net.model') # 将该模型存储

# 预测并还原结果
x = ((data[feature] - data_mean[feature])/data_std[feature]).as_matrix()
data[u'y_pred'] = model.predict(x) * data_std['y'] + data_mean['y']
#保存的表名命名格式为“2_2_3_1k此表功能名称”，是此小节生成的第1张表格，功能为revenue：增值税预测结果
data.to_excel('2_2_3_1zengzhi.xlsx')


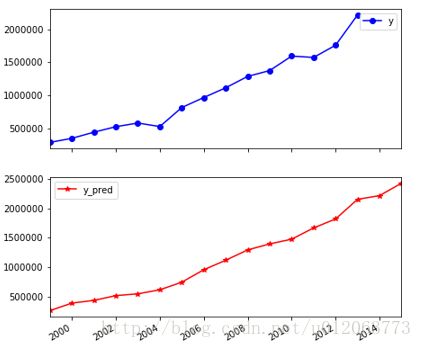
import matplotlib.pyplot as plt # 画出预测结果图
plt.rc('figure',figsize=(7,7))
p = data[['y','y_pred']].plot(subplots = True, style=['b-o', 'r-*'])
plt.savefig('zengzhi.jpg')
plt.show()

data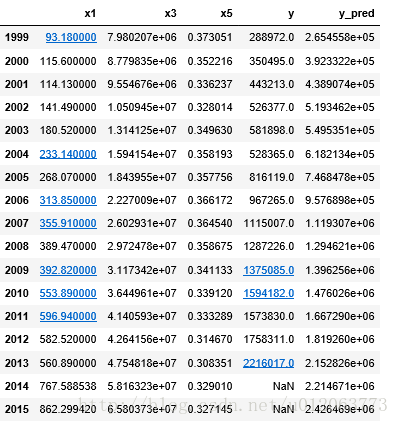

备注，本章节完整代码请见：点击打开链接