一文搞懂三角网格(Triangle Mesh)

三角网格的数据结构：
(1). 描述顶点位置的信息，$V=\{v_1,v_2,\dots ,v_n\}$。其中$v_i\in R^3$。
(2). 描述三角面片的信息，$F=\{f_1,f_2,\dots ,f_m\}$。其中$f_i$表示顶点的位置索引
除了这些必要信息，还可以包含诸如法向、纹理坐标等附加信息。
1. obj数据结构
比如应用最广泛的OBJ文件格式，表示一个立方体的文件内容如下：
file: cube.obj

# List of geometric vertices, with (x, y, z [,w]) coordinates, w is optional and defaults to 1.0.
v 1.000000 -1.000000 -1.000000
v 1.000000 -1.000000 1.000000
v -1.000000 -1.000000 1.000000
v -1.000000 -1.000000 -1.000000
v 1.000000 1.000000 -0.999999
v 0.999999 1.000000 1.000001
v -1.000000 1.000000 1.000000
v -1.000000 1.000000 -1.000000
# List of texture coordinates, in (u, [,v ,w]) coordinates, these will vary between 0 and 1. v, w are optional and default to 0.
vt 1.000000 0.333333
vt 1.000000 0.666667
vt 0.666667 0.666667
vt 0.666667 0.333333
vt 0.666667 0.000000
vt 0.000000 0.333333
vt 0.000000 0.000000
vt 0.333333 0.000000
vt 0.333333 1.000000
vt 0.000000 1.000000
vt 0.000000 0.666667
vt 0.333333 0.333333
vt 0.333333 0.666667
vt 1.000000 0.000000
# List of vertex normals in (x,y,z) form; normals might not be unit vectors.
vn 0.000000 -1.000000 0.000000
vn 0.000000 1.000000 0.000000
vn 1.000000 0.000000 0.000000
vn -0.000000 0.000000 1.000000
vn -1.000000 -0.000000 -0.000000
vn 0.000000 0.000000 -1.000000
# Polygonal face element (see below)
f 2/1/1 3/2/1 4/3/1
f 8/1/2 7/4/2 6/5/2
f 5/6/3 6/7/3 2/8/3
f 6/8/4 7/5/4 3/4/4
f 3/9/5 7/10/5 8/11/5
f 1/12/6 4/13/6 8/11/6
f 1/4/1 2/1/1 4/3/1
f 5/14/2 8/1/2 6/5/2
f 1/12/3 5/6/3 2/8/3
f 2/12/4 6/8/4 3/4/4
f 4/13/5 3/9/5 8/11/5
f 5/6/6 1/12/6 8/11/6

1.1 几何顶点：
以字母v开头指定顶点。后面是(x,y,z[, w])坐标。w是可选的，默认为1.0。
1.2 三角面片：
以字母f开头指定三角面片。面是使用顶点、纹理和法线的索引来定义的，格式为：

vertex_index/texture_index/normal_index

其中索引从1开始。
1.3 法向量：
以字母vn开头，后面添加x y z作为空间向量。某个平面上的法向量的计算可以通过平面上任意两个不相关向量的差积，然后单位化来获得。
1.4 对象名和多边形组名
一个OBJ文件可能包含多个物体对象，每个对象又由多个多边形组成。

o [object name]

g [group name]

比如：

o cube
v 1.0 -1.0 -1.0 1.0
v 1.0 -1.0 1.0 1.0
v -1.0 -1.0 1.0 1.0
v -1.0 -1.0 -1.0 1.0
v 1.0 1.0 -1.0 1.0
v 1.0 1.0 1.0 1.0
v -1.0 1.0 1.0 1.0
v -1.0 1.0 -1.0 1.0

g cube_bottom
f 1 2 3
f 3 4 1
g cube_top
f 5 6 7
f 7 8 5
g cube_front
f 6 2 3
f 3 7 6
g cube_rear
f 5 1 4
f 4 8 5
g cube_left
f 3 7 4
f 7 8 4
g cube_right
f 1 2 6
f 6 5 1

1.5 平滑着色
平滑着色指跨多边形的边界着色，默认情况下平滑着色是关闭的。
1.6 引用材料：
.mtl文件用于存储.obj文件访问的材料定义。比如木头、粗铁、黄铜等材料的定义。
一个.mtl文件可以定义多个材料，材料定义的格式：

newmtl [material name]
Ka r g b		#材质的环境颜色
Kd r g b		#材质的漫反射颜色
Ks r g b		#材质的镜面反射颜色
d alpha			#材质的透明度，默认值为1.0(完全不透明)，与Tr完全相反。
Tr alpha		#材质的透明度，默认值为0.0(完全不透明)，与d完全相反
Ns s			#材质的光泽度，默认值为0.0
illum n			#材质的光照模型，illum=1表示材质没有高光，不需要Ks值。illum=2表示材质存在镜面高光，需要指定Ks值。
map_Ka file	#环境颜色纹理贴图文件
map_Kd file	#漫反射纹理贴图文件
map_Ks file	#高光反射纹理贴图文件
map_d file	#透明纹理贴图
map_bump file
bump file	#凹凸贴图
disp file	#置换贴图
decal file	#模板贴花纹理

比如：
file:cube.mtl

newmtl wood
Ka  0.5000  0.5000  0.5000
Kd  1.0000  1.0000  1.0000
illum 1

newmtl iron
Ka  0.1985  0.0000  0.0000
Kd  0.5921  0.0167  0.0000
Ks  0.5973  0.2083  0.2083
illum 2
Ns 100.2235

newmtl copper
Ka  0.0394  0.0394  0.3300
Kd  0.5420  0.6420  0.1500
illum 1
Tr 0.4300

在.obj中导入.mtl文件语法：

mtllib [filename.mtl]

使用材料的语法：

usemtl [material name]

例如：
file: cube.obj

mtllib cube.mtl
o cube
v 1.0 -1.0 -1.0 1.0
v 1.0 -1.0 1.0 1.0
v -1.0 -1.0 1.0 1.0
v -1.0 -1.0 -1.0 1.0
v 1.0 1.0 -1.0 1.0
v 1.0 1.0 1.0 1.0
v -1.0 1.0 1.0 1.0
v -1.0 1.0 -1.0 1.0

g cube_bottom
usemtl wood
f 1 2 3
f 3 4 1
g cube_top
usemtl iron
f 5 6 7
f 7 8 5
g cube_front
usemtl copper
f 6 2 3
f 3 7 6
g cube_rear
usemtl wood
f 5 1 4
f 4 8 5
g cube_left
usemtl iron
f 3 7 4
f 7 8 4
g cube_right
usemtl copper
f 1 2 6
f 6 5 1

渲染结果：

使用纹理贴图必须先定义纹理坐标，比如mtl中wood使用了纹理贴图：

newmtl wood
Ka  0.5000  0.5000  0.5000
Kd  1.0000  1.0000  1.0000
illum 1
map_Kd wood.png

定义纹理坐标并在三角面片顶点中使用：

mtllib cube.mtl
o cube
v 1.0 -1.0 -1.0 1.0
v 1.0 -1.0 1.0 1.0
v -1.0 -1.0 1.0 1.0
v -1.0 -1.0 -1.0 1.0
v 1.0 1.0 -1.0 1.0
v 1.0 1.0 1.0 1.0
v -1.0 1.0 1.0 1.0
v -1.0 1.0 -1.0 1.0
vt 0.0 0.0
vt 0.0 1.0
vt 1.0 0.0
vt 1.0 1.0
usemtl wood
g cube_bottom
f 1/4 2/3 3/1
f 3/1 4/2 1/4
g cube_top
f 5/4 6/3 7/1
f 7/1 8/2 5/4
g cube_front
f 6/4 2/3 3/1
f 3/1 7/2 6/4
g cube_rear
f 5/4 1/3 4/1
f 4/1 8/2 5/4
g cube_left
f 3/1 7/3 4/2
f 7/3 8/4 4/2
g cube_right
f 1/1 2/3 6/2
f 6/3 5/4 1/2

最终渲染结果：

本节参考：
https://en.wikipedia.org/wiki/Wavefront_.obj_file

2. 三角网格的半边表示
上文讨论的三角网格模型仅仅适用于绘制。当需要对三角网格进行遍历和处理时，往往效率比较低。比如：检索包含某个顶点的所有面，往往需要遍历所有的面才能判断是否包含该点。
半边(half-edge)结构也称为双向链接边表(Doubly Connected Edge List, DCEL)，其基本思想是：

把每条无向边拆分成两条方向相反的边(即，半边)。

2.1 顶点
半边结构中的每个顶点至少需要包含两部分信息：
(1). 顶点的空间坐标信息。
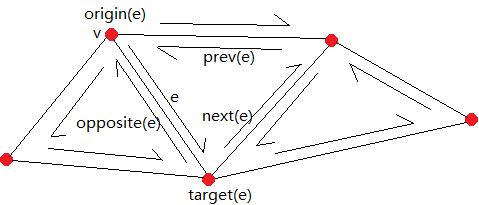
(2). 从该点出发的边，比如图中所示的v点，可以保存e，也可以保存其他任何从v出发的边。

2.2 半边
半边结构中每条半边(如图中的e)需要存储的信息如下：
(1). 该半边的源顶点origin(e)
(2). 该半边在同一个三角形中的下一个半边next(e)
(3). 该半边的对边opposite(e)
(4). 该半边所属的面IncFace(e)(即图中的中间三角形)。

半边结构中一些重要的公式：
prev(e)=next(next(e))
target(e)=origin(next(e))

$$TODO:半边结构的代码实现$$