机器学习入门——线性回归

什么是线性回归？

看我

单因子线性回归

简单实例

简单说就是为了求y=ax+b中的a和b

假设我们有一份数据如下：

首先，我们需要查看数据的相关性，以确保我们选择的变量与目标变量之间存在一定的线性关系。
我们先看一下这些数据的分布：

from matplotlib import pyplot as plt
# 输入数据
x = [1,2,3,4,5,6,7,8,9,10]
y = [7,9,11,13,15,17,19,21,23,25]

# 生成一个画布，设置坐标轴的比例
plt.figure(figsize=(5,5))

# 创建散点图
plt.scatter(x,y)

# 显示图形
plt.show()

建立线性回归模型

要对上述数据使用线性回归算法进行拟合，需要用到scikit-learn库。

scikit-learn是一个适用于python语言的、专门针对于机器学习应用的算法库。

使用sklearn.linear_model库中的线性回归算法进行拟合的示例代码：

from sklearn.linear_model import LinearRegression
import numpy as np

# 输入数据
x = [1,2,3,4,5,6,7,8,9,10]
y = [7, 9, 11, 13, 15, 17, 19, 21, 23, 25]

# 把x从一维转为二维
x = np.array(x)
x = x.reshape(-1,1)

# 建立线性回归模型
model = LinearRegression()

# 训练模型
model.fit(x, y)

# 获得y=ax+b中的a和b
a=model.coef_
b=model.intercept_
print(a)
print(b)

# 预测
x_new = [[11], [12], [13], [14], [15]]
y_pred = model.predict(x_new)

# 输出预测结果
print(y_pred)

注解：
在这个例子中，输入数据 x 和输出数据 y 分别被定义为两个列表。
然后，需要把x从一维转为二维，让x 中的每个元素是一个列表，包含一个自变量的值。 这是为了满足 LinearRegression() 函数的输入要求。否则会报错。
我们首先使用 LinearRegression() 函数初始化一个线性回归模型对象 model。
然后，我们使用模型对象的 fit() 方法训练模型，输入参数为 x 和 y。
然后，model.coef_获取系数，model.intercept_获取截距
最后，我们使用模型对象的 predict() 方法预测 x_new 中对应的因变量值 y_pred。
最后，我们输出预测结果。

评估模型表现

在上述代码的基础上添加如下代码：

from sklearn.metrics import mean_squared_error, r2_score

# 计算预测值与真实值之间的MSE
mse = mean_squared_error(y, model.predict(x))

# 计算决定系数R2
r2 = r2_score(y, model.predict(x))

# 输出MSE和R2
print("MSE:", mse)
print("R2:", r2)

注解：
我们使用 mean_squared_error 函数计算预测值与真实值之间的均方误差（MSE）。
我们使用 r2_score 函数计算模型的决定系数（R2）。
最后，我们输出计算得到的MSE和R2。

MSE越小越好，R2分数越接近1越好

可视化模型展示

在上述代码的基础上添加如下代码：

import matplotlib.pyplot as plt

# 绘制数据散点图
plt.scatter(x, y, color='black')

# 绘制拟合直线
plt.plot(x, model.predict(x), color='blue', linewidth=3)

# 添加图例
plt.legend(['Linear Regression Model', 'Data'])

# 添加坐标轴标签
plt.xlabel('X')
plt.ylabel('Y')

# 添加标题
plt.title('Linear Regression Model')

# 显示图形
plt.show()

注解：
我们使用 scatter 函数绘制数据散点图，其中 x 和 y 分别是自变量和因变量。
我们使用 plot 函数绘制线性回归模型的拟合直线，其中 x 和 model.predict(x) 分别表示自变量和对应的因变量预测值。
我们使用 legend 函数添加图例，其中 [‘Linear Regression Model’, ‘Data’] 分别表示拟合直线和数据散点图的标签。
我们使用 xlabel 和 ylabel 函数添加坐标轴标签。
我们使用 title 函数添加标题。
最后，我们使用 show 函数显示图形。

多因子线性回归

简单示例

基于usa_housing_price.csv数据,建立线性回归模型，预测合理房价:
1、以面积为输入变量，建立单因子模型,评估模型表现，可视化线性回归预测结果
2、以income、house age、 numbers of rooms、population、area为输入变量,建立多因子模型，评估模型表现
3、预测Income=65000,House Age=5,Number of Rooms=5,Population=30000,size=200的合理房价

这里是usa_housing_price.csv文件（不需要积分，可直接下载）

我们先看一下这些数据

import pandas as pd
import numpy as np

# 读取csv数据
data = pd.read_csv(r"C:\Users\HCSCI\Downloads\usa_housing_price.csv")

# 展示数据的前五行
data.head()

注解：
使用pandas.read_csv函数读取文件，注意到我们这里文件前有个r，作用是转义
上述代码执行结果如下：

首先，我们需要查看数据的相关性，以确保我们选择的变量与目标变量之间存在一定的线性关系。
在上述代码的基础上添加如下代码：

from matplotlib import pyplot as plt

# 创建图
fig = plt.figure(figsize=(10,10))

# 绘制第一幅子图
fig1 = plt.subplot(231)
# 绘制数据散点图
plt.scatter(data.loc[:,'Avg. Area Income'], data.loc[:,'Price'])
# 添加标题
plt.title('Price VS Income')

# 绘制第二幅子图
fig1 = plt.subplot(232)
# 绘制数据散点图
plt.scatter(data.loc[:,'Avg. Area House Age'], data.loc[:,'Price'])
# 添加标题
plt.title('Price VS House Age')

# 绘制第三幅子图
fig1 = plt.subplot(233)
# 绘制数据散点图
plt.scatter(data.loc[:,'Avg. Area Number of Rooms'], data.loc[:,'Price'])
# 添加标题
plt.title('Price VS Number of Rooms')

# 绘制第四幅子图
fig1 = plt.subplot(234)
# 绘制数据散点图
plt.scatter(data.loc[:,'Area Population'], data.loc[:,'Price'])
# 添加标题
plt.title('Price VS Population')

# 绘制第五幅子图
fig1 = plt.subplot(235)
# 绘制数据散点图
plt.scatter(data.loc[:,'size'], data.loc[:,'Price'])
# 添加标题
plt.title('Price VS size')

#显示图形
plt.show()

注解：
在绘制子图中，我们使用matplotlib中的subplot绘制子图，subplot(231)中参数231的含义为：子图一共两行三列，而该图为第一幅图。
在绘制散点图中，我们使用scatter函数，其参数如data.loc[:,‘size’]，其中:表示返回data数据的所有行、size表示size这一列的数据。
上述代码执行结果如下：

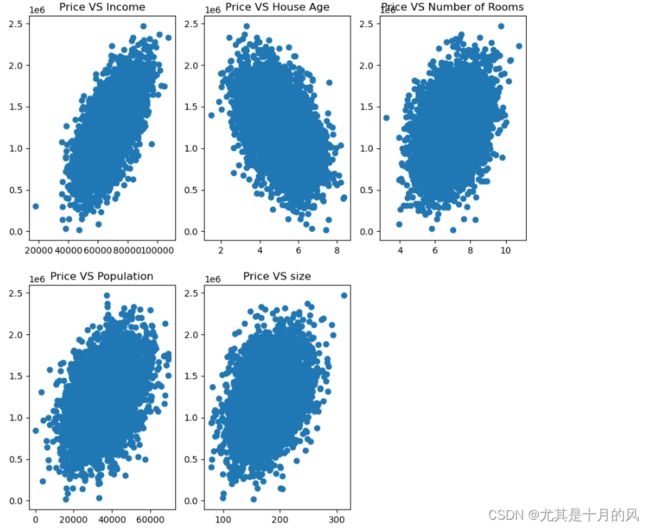
单因子

然后我们以面积为输入变量，建立单因子模型,评估模型表现，可视化线性回归预测结果

建立线性回归模型
在上述代码的基础上添加如下代码：

from sklearn.linear_model import LinearRegression
# 定义x和y
x = data.loc[:,'size']
y = data.loc[:,'Price']
# 把x变成二维
x = np.array(x).reshape(-1,1)

# 建立单因子模型
LR1 = LinearRegression()

# 训练模型
LR1.fit(x,y)

# 预测
y_predict_1 = LR1.predict(x)
print(y_predict_1)

评估模型表现
在上述代码的基础上添加如下代码：

from sklearn.metrics import mean_squared_error, r2_score

# 计算预测值与真实值之间的MSE
mse = mean_squared_error(y, y_predict_1)

# 计算决定系数R2
r2 = r2_score(y,y_predict_1)

# 输出MSE和R2
print("MSE:", mse)
print("R2:", r2)

可视化预测
在上述代码的基础上添加如下代码：

# 画布
fig6 = plt.figure(figsize=(8,5))
# 散点图
plt.scatter(x,y)
# 绘制拟合直线
plt.plot(x,y_predict_1,'r')
# 显示图
plt.show()

注解：
在绘制拟合直线中，我们使用plt.plot(x,y_predict_1,‘r’)，其参数中的r表示画红线red

上述代码执行结果如下:

分析可以发现，模型效果不好

建立线性回归模型

在上述代码的基础上添加如下代码：

# 构造多因子输入变量
x_mutil = data.drop(['Price'],axis=1)

# 创建第二个线性回归模型
LR_mutil = LinearRegression()

# 训练模型
LR_mutil.fit(x_mutil,y)

# 预测
y_predict_mutil = LR_mutil.predict(x_mutil)
print(y_predict_mutil)

注解：
在构造多因子变量时，我们的输入变量是五列，所以可以直接把Price那一列给删掉。使用drop函数即可。参数解释：['Price']：要删除的列的名称。axis=1：指定删除的方向，这里是删除列，因此 axis=1。

评估模型表现

在上述代码的基础上添加如下代码：

from sklearn.metrics import mean_squared_error, r2_score

# 计算预测值与真实值之间的MSE
mse = mean_squared_error(y, y_predict_mutil)

# 计算决定系数R2
r2 = r2_score(y, y_predict_mutil)

# 输出MSE和R2
print("MSE:", mse)
print("R2:", r2)

可视化模型展示

由于我们有五个因子，没办法像之前一样画出x和y的关系，所以想要查看模型预测的效果，可以直接画出实际的y值和预测的y值，看看它是不是比较接近于一条直线，并且最好和x轴是呈一个45°角。

在上述代码的基础上添加如下代码：

# 画布
fig7 = plt.figure(figsize=(8,5))

# 散点图
plt.scatter(y, y_predict_mutil)

# 显示
plt.show()

代码执行结果如下：

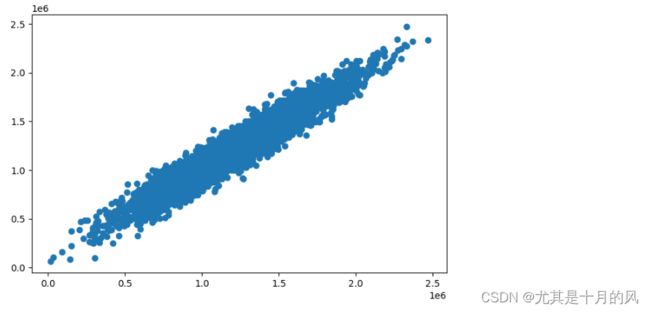
可以看到我们的集中度还是不错的，越集中越好，可以和我们前面的单因子图进行对比，单因子很离散。所以当前模型的效果还是不错的。

预测

预测Income=65000,House Age=5,Number of Rooms=5,Population=30000,size=200的合理房价

x_test = [65000,5,5,30000,200]
x_test = np.array(x_test).reshape(1,-1)
print(x_test)

y_test_predict = LR_mutil.predict(x_test)
print(y_test_predict)

注解：
这里执行可能会报警告，但是也可以执行出结果。

这个警告信息通常是因为在使用sklearn的某些模型时，传递给模型的特征矩阵X没有列名（即特征名）。这可能会导致一些问题，例如在解释模型时无法识别哪些特征对目标变量的预测有重要影响。

解决这个问题的方法有两种

• 你可以在创建LinearRegression模型时设置参数fit_intercept=False，这将禁用警告。
  model = LinearRegression(fit_intercept=False)。
• 为X设置列名，如下：

# 创建一个特征矩阵X
x = [65000,5,5,30000,200]
x = np.array(x).reshape(1,-1)

# 创建一个特征名列表feature_names，长度应该与X的列数相同
feature_names = ['Avg. Area Income','Avg. Area House Age','Avg. Area Number of Rooms','Area Population','size']

# 将X转换为DataFrame，并设置列名
x_test = pd.DataFrame(x, columns=feature_names)
print(x_test)

y_test_predict = LR_mutil.predict(x_test)
print(y_test_predict)