十道经典面试算法真题详解
前言
分享一下 腾讯常考的十道算法题(真题)。在金三银四,希望对大家有帮助呀。
-
重排链表
-
最长递增子序列
-
环形链表
-
反转链表
-
最长回文子串
-
全排列
-
LRU 缓存
-
合并K个升序链表
-
无重复字符的最长子串
-
删除链表的倒数第 N 个结点
1. 重排链表
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
输入:
head = [1,2,3,4]
输出:
[1,4,2,3]
思路:
如果是数组就好了,哈哈,因为数组可以直接通过下标访问,很容易就可以解答这道题了。但是这是链表。**链表不支持下标访问,**我们没办法随机访问到链表任意位置的元素,怎么办呢?
我们可以先遍历一下,用数组把链表的元素按顺序存储起来呀,然后就可以把它当做数组这么访问来用了对吧,最后重建下链表即可啦。
ArrayList的底层就是数组,我们先用它存储链表就好,如下:
List<ListNode> list = new ArrayList<ListNode>();
ListNode node = head;
while (node != null) {
list.add(node);
node = node.next;
}
有了一个数组结构的链表后,如何重建链表呢?回头多看示例两眼,很容易就发小规律啦:先排第1个,再排倒数第1个,接着排第2个,紧接着倒数第2个。显然这个规律很明显,代码也比较好实现:
int i = 0;
int j = list.size()-1;
while(i<j){
list.get(i).next = list.get(j);
i++;
if(i==j){
break;
}
list.get(j).next = list.get(i);
j--;
}
//大家画个图就很清晰知道为什么需要这行了,哈哈
list.get(i).next = null;
完整实现代码如下:
class Solution {
public void reorderList(ListNode head) {
if (head == null) {
return;
}
List<ListNode> list = new ArrayList<ListNode>();
ListNode node = head;
while (node != null) {
list.add(node);
node = node.next;
}
int i = 0, j = list.size() - 1;
while (i < j) {
list.get(i).next = list.get(j);
i++;
if (i == j) {
break;
}
list.get(j).next = list.get(i);
j--;
}
list.get(i).next = null;
}
}
2. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
实例1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
实例2:
输入:nums = [0,1,0,3,2,3]
输出:4
思路:
这道题是求最值问题,可以使用动态规划解决。动态规划的解题整体思路就是:
-
穷举分析
-
分析找规律,拆分子问题
-
确定边界
-
确定最优子结构
-
写出状态转移方程
2.1 穷举分析
动态规划的核心思想包括拆分子问题,记住过往,减少重复计算。所以我们在思考原问题:数组num[i]的最长递增子序列长度时,可以思考下相关子问题,比如原问题是否跟子问题num[i-1]的最长递增子序列长度有关呢?
自底向上的穷举过程:
-
当nums只有一个元素10时,最长递增子序列是[10],长度是1.
-
当nums需要加入一个元素9时,最长递增子序列是[10]或者[9],长度是1。
-
当nums再加入一个元素2时,最长递增子序列是[10]或者[9]或者[2],长度是1。
-
当nums再加入一个元素5时,最长递增子序列是[2,5],长度是2。
-
当nums再加入一个元素3时,最长递增子序列是[2,5]或者[2,3],长度是2。
-
当nums再加入一个元素7时,,最长递增子序列是[2,5,7]或者[2,3,7],长度是3。
-
当nums再加入一个元素101时,最长递增子序列是[2,5,7,101]或者[2,3,7,101],长度是4。
-
当nums再加入一个元素18时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4。
-
当nums再加入一个元素7时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4.
2.2 分析找规律,拆分子问题
通过上面分析,我们可以发现一个规律:
如果新加入一个元素nums[i], 最长递增子序列要么是以nums[i]结尾的递增子序列,要么就是nums[i-1]的最长递增子序列。看到这个,是不是很开心,nums[i]的最长递增子序列已经跟子问题 nums[i-1]的最长递增子序列有关联了。
原问题数组nums[i]的最长递增子序列 = 子问题数组nums[i-1]的最长递增子序列/nums[i]结尾的最长递增子序列
是不是感觉成功了一半呢?但是如何把nums[i]结尾的递增子序列也转化为对应的子问题呢?要是nums[i]结尾的递增子序列也跟nums[i-1]的最长递增子序列有关就好了。又或者nums[i]结尾的最长递增子序列,跟前面子问题num[j](0=
nums[i]的最长递增子序列,不就是从以数组num[i]每个元素结尾的最长子序列集合,取元素最多(也就是长度最长)那个嘛,所以原问题,我们转化成求出以数组nums每个元素结尾的最长子序列集合,再取最大值嘛。哈哈,想到这,我们就可以用dp[i]表示以num[i]这个数结尾的最长递增子序列的长度啦,然后再来看看其中的规律:
其实,nums[i]结尾的自增子序列,只要找到比nums[i]小的子序列,加上nums[i] 就可以啦。显然,可能形成多种新的子序列,我们选最长那个,就是dp[i]的值啦
-
nums[3]=5,以5结尾的最长子序列就是[2,5],因为从数组下标0到3遍历,只找到了子序列[2]比5小,所以就是[2]+[5]啦,即dp[4]=2
-
nums[4]=3,以3结尾的最长子序列就是[2,3],因为从数组下标0到4遍历,只找到了子序列[2]比3小,所以就是[2]+[3]啦,即dp[4]=2
-
nums[5]=7,以7结尾的最长子序列就是[2,5,7]和[2,3,7],因为从数组下标0到5遍历,找到2,5和3都比7小,所以就有[2,7],[5,7],[3,7],[2,5,7]和[2,3,7]这些子序列,最长子序列就是[2,5,7]和[2,3,7],它俩不就是以5结尾和3结尾的最长递增子序列+[7]来的嘛!所以,dp[5]=3 =dp[3]+1=dp[4]+1。
很显然有这个规律:一个以nums[i]结尾的数组nums
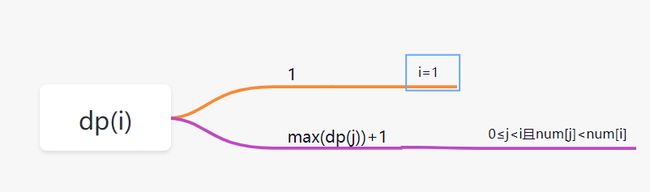
- 如果存在j属于区间[0,i-1],并且num[i]>num[j]的话,则有:dp(i) =max(dp(j))+1。
2.3 确定边界
当nums数组只有一个元素时,最长递增子序列的长度dp(1)=1,当nums数组有两个元素时,dp(2) =2或者1, 因此边界就是dp(1)=1。
2.4 确定最优子结构
从2.2 穷举分析找规律,我们可以得出,以下的最优结构:
dp(i) =max(dp(j))+1,存在j属于区间[0,i-1],并且num[i]>num[j]。
max(dp(j)) 就是最优子结构。
2.5 写出状态转移方程
通过前面分析,我们就可以得出状态转移方程啦:
所以数组nums[i]的最长递增子序列就是:
最长递增子序列 =max(dp[i])
完整代码实现如下:
class Solution {
public int lengthOfLIS(int[] nums) {
if (nums.length == 0) {
return 0;
}
int[] dp = new int[nums.length];
//初始化就是边界情况
dp[0] = 1;
int maxans = 1;
//自底向上遍历
for (int i = 1; i < nums.length; i++) {
dp[i] = 1;
//从下标0到i遍历
for (int j = 0; j < i; j++) {
//找到前面比nums[i]小的数nums[j],即有dp[i]= dp[j]+1
if (nums[j] < nums[i]) {
//因为会有多个小于nums[i]的数,也就是会存在多种组合了嘛,我们就取最大放到dp[i]
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
//求出dp[i]后,dp最大那个就是nums的最长递增子序列啦
maxans = Math.max(maxans, dp[i]);
}
return maxans;
}
}
3. 环形链表
给定一个链表的头节点head ,返回链表开始入环的第一个节点。如果链表无环,则返回 null。
实例:
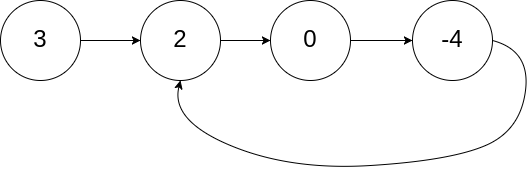
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
如果判断链表是否有环,我们可以使用快慢指针,快指针是慢指针速度的两倍,当两个指针相遇时,即表示有环。
boolean hasCycle(ListNode head ){
ListNode slow = head;
ListNode fast = head;
while(fast!=null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
if(fast==slow){
return true;
}
}
return false;
}
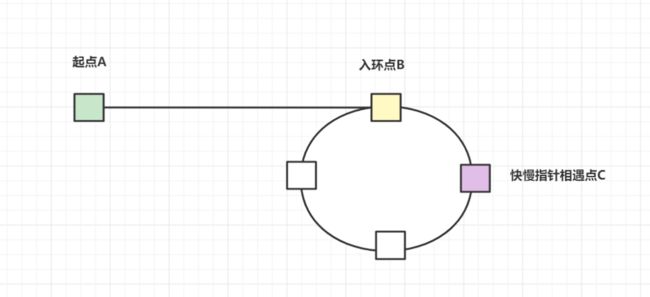
我们可以很容易就判断有环,但是如何返回入环的第一个节点呢?我们来画个图分析一波:
假设起点为A,入环点为B,快慢指针相遇点为C,慢指针走到相遇点为k步,B到C的距离为m。设环型周长为X。因为快指针速度是慢指针的2倍。则有:
K-m + X + m = 2K = 快指针走的举例
所以周长X = K。相遇后,快指针到继续往前走,走到入环点B,刚好距离是X-m = K-m。而起点到B节点,距离也是K-m。因此,快慢指针相遇后,慢指针回到起点,这时候快慢指针一样的速度走,相遇时,就是入环点啦,是不是无巧不成书呀,哈哈哈。
完整代码如下:
public class Solution {
public ListNode detectCycle(ListNode head) {
if(head ==null){
return null;
}
ListNode fast = head;
ListNode slow = head;
while(fast!=null&&fast.next!=null){
fast = fast.next.next;
slow = slow.next;
//快慢指针相等表示有环
if(slow==fast){
//回到起点一起相同速度走
while(head!=fast){
head = head.next;
fast = fast.next;
}
return head;
}
}
return null;
}
}
4. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
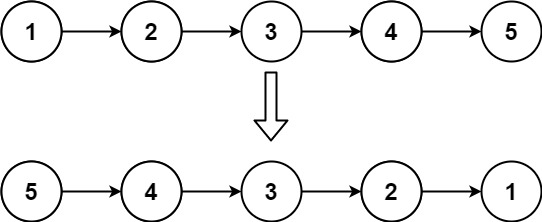
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
完整代码如下:
class Solution {
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode next = head;
ListNode curr = head ;
while(curr!=null){
next = curr.next ;
curr. next = prev;
prev = curr ;
curr = next ;
}
return prev;
}
}
之前图解过这道题,大家可以看下哈:
看一遍就理解,图解单链表反转
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
实例1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
这道题可以使用中心扩展法实现,从中间开始向两边扩散来判断回文串。
for 0 <= i < len(s):
找到以 s[i] 为中心的回文串
更新答案
但是回文串可能是长度可能是奇数,也可能是偶数,因此需要加多一步:
for 0 <= i < len(s):
找到以 s[i] 为中心的回文串
找到以 s[i] 和s[i+1] 为中心的回文串
更新答案
完整代码如下:
class Solution {
public String longestPalindrome(String s) {
if(s==null|| s.length()<2){
return s;
}
String result ="";
for(int i=0;i<s.length();i++){
String r1 = subLongestPalindrome(s,i,i);
String r2 = subLongestPalindrome(s,i,i+1);
String tempMax= r1.length()>r2.length()? r1 :r2;
result = tempMax.length()> result.length()?tempMax:result;
}
return result;
}
private String subLongestPalindrome(String s,int l,int r){
while(l>=0&&r<s.length()&&s.charAt(l)==s.charAt(r)){
l--;
r++;
}
return s.substring(l+1,r);
}
}
6.全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
这道题可以用回溯算法解决,完整代码如下:
class Solution {
//全排列,即所有路径集合
List<List<Integer>> allPath = new LinkedList<>();
public List<List<Integer>> permute(int[] nums) {
//当前路径,入口路径,path是空的
List<Integer> path = new LinkedList<>();
//递归函数入口,可做选择是nums数组
backTrace(nums,path);
return allPath;
}
public void backTrace(int[] nums,List<Integer> path){
//已走路径path的数组长度等于nums的长度,表示走到叶子节点,所以加到全排列集合
if(nums.length==path.size()){
allPath.add(new LinkedList(path));
return;
}
for(int i=0;i<nums.length;i++){
//剪枝,排查已经走过的路径
if(path.contains(nums[i])){
continue;
}
//做选择,加到当前路径
path.add(nums[i]);
//递归,进入下一层的决策
backTrace(nums,path);
//取消选择
path.remove(path.size() - 1);
}
}
}
大家可以看下这篇回溯文章哈,有回溯算法的框架套用。
面试必备:回溯算法详解
7. LRU 缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
-
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
-
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
-
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以O(1) 的平均时间复杂度运行。
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
这道题,出现的频率还是挺高的,很多小伙伴在面试时,都反馈自己遇到过原题。
LRU,Least Recently Used,即最近使用过的数据是有用的,可以使用双链表+Hashmap解答,双链表用于存储LRUCache的数据,Hashmap实现O(1)的平均时间复杂度。
-
每次从链表尾部添加元素,靠尾的元素就是最近使用过
-
某个key可以通过哈希表快速定位到节点。
对于双链表,需要做哪些事呢。
-
首先是链表初始化,为了方便处理i,虚拟一个头节点和尾结点。
-
添加元素时,放到链表的尾部,表示该元素最近使用过
-
删除双向链表的某个节点
-
删除并返回头节点,表示删除最久未使用的元素
-
返回链表当前长度
LRU缓存有哪些方法
-
构造函数初始化方法
-
get和put方法
-
makeRecently 设置某个元素最近使用过的方法,哈希表已经有该元素
-
addRecently 添加最近使用过的元素,同时更新map
-
deleteKey 删除某个key对应的元素,同时删除map上的节点
-
removeLeastRecently 删除最久未使用的元素
完整代码如下:
class Node {
int key,val;
Node next,prev;
public Node(int key,int val){
this.key = key;
this.val = val;
}
}
class DoubleList {
//虚拟出头节点和尾结点
private Node head, tail;
private int size;
//初始化双链表
public DoubleList() {
//虚拟头结点
head = new Node(0, 0);
//虚拟头结点
tail = new Node(0, 0);
head.next = tail;
tail.prev = head;
size = 0;
}
//要加到链表尾部,且越靠近链表尾部,越表示最近使用过
public void addLast(Node x) {
//比如当前链表为:head <-> 1 <-> tail,加入结点x = 2
x.prev = tail.prev;
// 完成结点2指向两端的箭头 head <-> 1 <- 2 -> tail; 此时tail.pre = 结点1还未断开
x.next = tail;
//head <-> 1 <-> 2 -> tail;
tail.prev.next = x;
//head <-> 1 <-> 2 <-> tail;
tail.prev = x;
//更新链表长度
size++;
}
// 删除指定结点
public void remove(Node x) {
x.prev.next = x.next;
x.next.prev = x.prev;
size--;
}
// 删除并返回头结点
public Node removeHead() {
if (head.next == tail) {
return null;
}
Node first = head.next;
// size在remove中更新了
remove(first);
// 用作在哈希表中移除最久未使用的数据值
return first;
}
// 获取链表长度
public int getSize() {
return size;
}
}
public class LRUCache {
private Map<Integer, Node> map;
private DoubleList doubleList;
private int cap;
public LRUCache(int capacity) {
this.map = new HashMap<>();
this.doubleList = new DoubleList();
this.cap = capacity;
}
public int get(int key) {
if (map.containsKey(key)) {
// 先将key标记为最近使用,再返回value
makeRecently(key);
return map.get(key).val;
} else {
return -1;
}
}
public void put(int key, int value) {
if (map.containsKey(key)) {
deleteKey(key); // 从原map中移除该key
addRecently(key, value); // 更新最近使用
return;
}
int size = doubleList.getSize();
if (size == cap) { // 说明需要移除最久未使用的元素了
removeLeastRecently();
}
addRecently(key, value); //添加新的元素进来
}
public void makeRecently(int key) { // 将某个key标记为最近使用的元素(map中已存在的)
Node x = map.get(key);
doubleList.remove(x); // 先从双链表删除
doubleList.addLast(x); // 再添加到链表末尾, 因为尾部是最近使用过的元素
}
public void addRecently(int key, int value) { // 添加最近使用过的元素
Node x = new Node(key, value);
doubleList.addLast(x);
map.put(key, x); //更新map
}
public void deleteKey(int key) {
Node x = map.get(key);
map.remove(key);
doubleList.remove(x); // 在map中和cache中同时删除
}
// 删除最久未使用的元素
public void removeLeastRecently() {
// 最久未使用的一定在链表头部
Node oldNode = doubleList.removeHead();
int oldKey = oldNode.key;
map.remove(oldKey);
}
}
8. 合并K个升序链表
给你一个链表数组,每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
合并两个有序链表,是比较简单的,相信大家都会做。那么如何合并K个有序链表呢?其实道理是一样的,我们可以借用优先级队列找出最小节点,完整代码如下:
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if(lists.length==0){
return null;
}
//虚拟节点
ListNode head = new ListNode(0);
ListNode tail = head;
//优先队列
PriorityQueue<ListNode> queue = new PriorityQueue<>(lists.length,(a, b)->(a.val-b.val));
//将K个链表头节点合并最小堆
for (ListNode node: lists) {
if (node != null) {
queue.add(node);
}
}
while (!queue.isEmpty()) {
//获取最小节点,放到结果链表中
ListNode node = queue.poll();
tail.next = node;
if (node.next != null) {
queue.add(node.next);
}
//指针链表一直往前
tail = tail.next;
}
return head.next;
}
}
9. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
这道题可以使用滑动窗口来实现。滑动窗口就是维护一个窗口,不断滑动,然后更新答案。
滑动窗口的大致逻辑框架,伪代码如下:
int left =0,right = 0;
while (right < s.size()){
//增大窗口
window.add(s[right]);
right++;
while (window needs shrink){
//缩小窗口
window.remove (s[left]);
left ++;
}
}
解法流程如下:
-
首先呢,就是获取原字符串的长度。
-
接着维护一个窗口(数组、哈希、队列)
-
窗口一步一步向右扩展
-
窗口在向右扩展滑动过程,需要判断左边是否需要缩减
-
最后比较更新答案
完整代码如下:
int lengthOfLongestSubstring(String s){
//获取原字符串的长度
int len = s.length();
//维护一个哈希集合的窗口
Set<Character> windows = new HashSet<>();
int left=0,right =0;
int res =0;
while(right<len){
char c = s.charAt(right);
//窗口右移
right++;
//判断是否左边窗口需要缩减,如果已经包含,那就需要缩减
while(windows.contains(c)){
windows.remove(s.charAt(left));
left++;
}
windows.add(c);
//比较更新答案
res = Math.max(res,windows.size());
}
return res;
}
之前写过一篇滑动窗口解析,大家有兴趣可以看下哈:
leetcode必备算法:聊聊滑动窗口
10.删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 :
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
这道题可以使用双指针解决。既然我们要找到倒数第n个节点,我们可以使用两个指针first 和 second同时对链表进行遍历,并且first 比second超前 n个节点。当 first遍历到链表的末尾时,second 就恰好处于倒数第n个节点。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0, head);
ListNode first = head;
ListNode second = dummy;
//first 比second先走n个节点
for (int i = 0; i < n; ++i) {
first = first.next;
}
//直到走到链表尾部
while (first != null) {
first = first.next;
second = second.next;
}
//删除节点
second.next = second.next.next;
ListNode ans = dummy.next;
return ans;
}
}