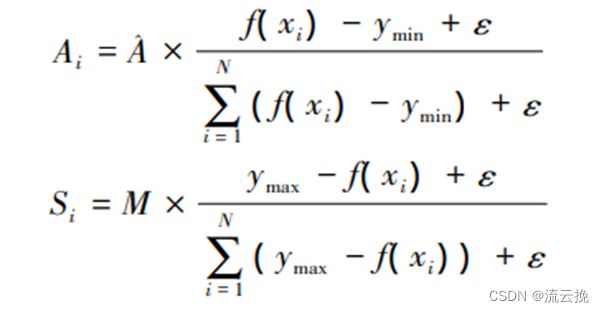多目标烟花算法原理和解析
上文介绍了烟花算法的基本代码解析,至于基本的烟花算法在CSDN里面有不少大佬介绍过,我就对这一部分内容进行更一层次的介绍。
但是大多都是对单目标进行讲解,今天对多目标烟花算法进行一个介绍。
多目标烟花算法和其他的多目标算法本质相同,可以通过两种方式达到多目标优化的目的。
一种是采用多目标转单目标的形式,将多个目标进行权重分配构成一个单目标,然后再用单目标烟花算法去求解模型。
二是采用帕勒托计算方式的方法去求解多目标优化问题。
本文主要针对第二种方式进行介绍。
求解帕勒托前沿的方式方法在CSDN和期刊文献上有不少的介绍,感兴趣可以去查找相关资料。
多目标烟花算法由同样是以爆炸算子、变异算子和选择策略组成
爆炸算子:
其中A和M为常数,调整爆炸半径和火花数目
变异算子:
e为方差为1、均值为1的高斯分布
选择策略:使烟花种群中优秀的信息能够传递到下一代种群中,烟花被选择的概率如下
以上所有的公式可以根据自己案例的需求进行改进,本文就不深入介绍了。
注意:在多目标烟花算法中,与单目标的不同点在于输出变量,单目标输出变量上为一个常数,而多目标在输出参数上为一个矩阵。
如何求解通过多目标求解最优?
在多目标烟花算法中,前期和正常的烟花算法一样,需要进行爆炸和变异,其中本文所采用的爆炸方式为增强烟花算法的坐标轴爆炸方式:
作者认为该种烟花爆炸方式虽然有缺点但是更适合多目标烟花算法,详细的参考文章可在知网上搜寻增强烟花算法论文和期刊。
在寻优过程中,不可缺少的是帕勒托支配法,通过比较支配强度找出烟花算法的帕勒托前沿。
相关流程图如下:
相关的帕勒托支配算法如下:
function [RANK] = FastNonDominatedSorting_Vectorized(fitness)%重点
% Initialization初始化
Np = size(fitness,1);
RANK = zeros(Np,1);
current_vector = [1:1:Np]';
current_pf = 1;
all_perm = [repmat([1:1:Np]',Np',1), reshape(repmat([1:1:Np],Np,1),Np^2,1)];%所有种群两两组合
all_perm(all_perm(:,1)==all_perm(:,2),:) = [];%若有自己与自己重复的则删除
% Computing each Pareto Front
while ~isempty(current_vector)%判断(矩阵)是否为空 如果为非空,返回1,空返回0,不加取反符号 返回值相反
% Check if there is only a single particle
if length(current_vector) == 1
RANK(current_vector) = current_pf;
break;
end
% Non-dominated particles
% Note: nchoosek has an exponential grow in computation time, so
% it's better to take all the combinations including repetitions using a
% loops (quasi-linear grow) or repmats (linear grow)
%all_perm = nchoosek(current_vector,2);
%all_perm = [all_perm; [all_perm(:,2) all_perm(:,1)]];
d = dominates(fitness(all_perm(:,1),:),fitness(all_perm(:,2),:));%判断哪些是非支配者
dominated_particles = unique(all_perm(d==1,2));%去掉相同的
% Check if there is no room for more Pareto Fronts
% 判断是否所有解都被分配层级帕勒托前沿
if sum(~ismember(current_vector,dominated_particles)) == 0
break;
end
% Update ranks and current_vector
non_dom_idx = ~ismember(current_vector,dominated_particles);
RANK(current_vector(non_dom_idx)) = current_pf;
all_perm(ismember(all_perm(:,1),current_vector(non_dom_idx)),:) = [];
all_perm(ismember(all_perm(:,2),current_vector(non_dom_idx)),:) = [];
current_vector(non_dom_idx) = [];
current_pf = current_pf + 1;
end
endfunction d =dominates(x,y)
d = all(x <= y ,2 )& any(x < y , 2);%支配关系表达式,至少有一个y要比x好且所有的y都不能比x差,被支配者为1
end本文将以IEEE118节点为例进行仿真验证。
IEEE118系统是由54台发电机、118个节点和186条支路组成。其中包含15处节点补偿点和9处变压器调节支路。以69节点作为平衡点和基准电压点,进行无功优化。
实验以牛顿拉夫逊潮流分析为基础,在满足系统和发电机约束条件下,获取最优控制方案。
由于控制变量过多,本文只选择30个变量进行优化。
优化目标函数:有功网络损耗、节点电压偏差
编程与单目标类似由于文件过多,就不过多展示。
优化结果和多目标遗传与多目标粒子群做对比: