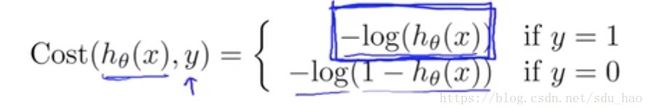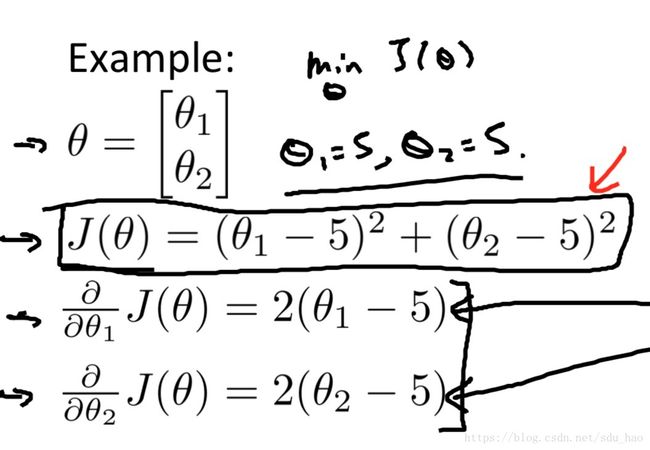机器学习 | 吴恩达机器学习第三周学习笔记

课程视频链接：https://www.coursera.org/learn/machine-learning/home/welcome

第三周PPT  下载密码:8o4e

上一篇博客主要介绍了第二周的课程的内容，包括多变量线性回归，使用梯度下降法求解多变量线性回归的实用技巧，特征缩放与模型特征选择并介绍了多项式回归，最后引入一种线性回归的解析解法并与梯度下降法进行比较。本篇博客将系统的介绍第三周的内容，本周主要讲解分类问题，引入了逻辑回归模型来解决分类问题，并详细的介绍了逻辑回归模型的细节，包括假设函数，代价函数，优化求解方法包括之前学习的梯度下降法和更高级的优化方法，以及多分类问题的探讨，最后介绍了过拟合问题，并以线性回归和逻辑回归为例讲解该问题的解决方法(正则化)。本章探讨的逻辑回归模型，是解决分类问题最基础但使用最广泛的方法，必须熟练掌握，之后还会介绍一些更强大的分类模型，所以本章内容尤为重要。

 

目录

 

一、分类和表示

1.分类问题

2.逻辑回归假设函数表达式

3.决策边界

二、逻辑回归模型

1.代价函数

2.简化代价函数和梯度下降法

3.高级优化方法

4.多分类问题

三、过拟合

1.过拟合问题

2.代价函数(正则化)

3.线性回归中的正则化

4.逻辑回归中的正则化

四、第三周编程实验

---

一、分类和表示

1.分类问题

（1）分类问题的例子

• 判断一个邮件是否是垃圾邮件
• 判断一个在线交易是否为诈骗
• 判断肿瘤是良性的还是恶性的

以上的这三个例子都是一个二分类的问题，他们的输出变量只有两个取值：

                                                

其中0代表负类(比如恶性肿瘤),1代表正类(比如良性肿瘤)。

在之后的学习中，我们还会介绍多分类问题，所谓多分类就是输出变量有多个取值。比如一个四分类问题: 

                                                

(2) 如何求解分类问题

假设我们现在有一个二分类的数据集，判断一个肿瘤是否为恶性的。我们将该训练集可视化，得到下图：

其中横轴为输入变量肿瘤大小，纵轴是输出变量，1代表为恶性肿瘤，0代表是良性。

最直观的做法，我们可能会采用之前学习的线性回归方法，比如用下图的这条洋红色直线来拟合该数据集：

并且我们为该分类器的输出设置一个阈值0.5:

 当时，预测为正类，即,是恶性肿瘤；

当时，预测为正类，即,是良性肿瘤。

此时我们将于阈值0.5在图上标出，它与直线有一个交点，该交点在x轴上有一个投影，对应一个肿瘤大小值。也就是说当肿瘤大小大于该值时，认为是恶性肿瘤；反之是良性的。

从上图的分类效果来看，用线性回归貌似取得了不错的分类效果。那么使用线性回归解决分类问题真的可行吗？我们接下来改变一个这个数据集，增加一个额外的样本，如下图右上方所示。此时由于该样本的存在，使用线性回归拟合该数据集，可能会得到下图中蓝色的线：

很显然，此时用线性回归来解决该分类问题是非常不合理的。所以用线性回归解决分类问题通常不是一个好的做法。

 

此外，如果我们使用线性回归解决分类问题还有一个有趣的事情。对于二分类问题，我们知道输出变量的取值只有两个0和1。但是当你使用线性回归时，的输出可能远大于1，即使你的训练样本的标签全为0；或者的输出可能小于0，即使你的训练样本的标签全为1。

所以接下来我们会介绍逻辑回归算法，该算法会使假设函数的输出介于0和1之间，输出值既不会远大于1也不会远小于0.

注意逻辑回归算法，虽然叫“回归”，但它是一个分类算法，不要混淆。

2.逻辑回归假设函数表达式

解决分类问题我们不能忽略其输出变量的取值是离散的，因此我们用线性回归来拟合数据集，给定预测，通常效果非常差；而且线性回归中的远大于1或远小于0是没有意义的，因为我们知道输出变量。

因此，为了修正这个问题，我们需要改变假设函数，使其值介于0和1之间。我们可以引入函数，将映射到0和1之间。

逻辑回归算法的假设函数表达式：

 

其中为函数，也叫函数，其图像如下图所示：

,且当时，;且当时，。

 

对于假设函数输出值的解释：

 = 在给定输入变量和参数的情况下，预测输出变量的概率。

比如：输入变量      假设函数；那么这种情况下，我们会告诉病人有70%的可能性认为该肿瘤是恶性的。

更正式的写法：

                                   

那么的概率可以由以下公式得到：

                                   

                                   

3.决策边界

我们接下来探讨一下逻辑回归算法的输出到底是什么，以及我们在何种情况下可以预测“”

逻辑回归假设函数：

                                    

我们认为：

                                    当时，预测；

                                    当时，预测。   

• 考虑下图所示的数据集：

其假设函数如下：

                                       

并且我们假设模型参数已经通过该训练集求出(具体的求解方法之后会讲),。

由之前的推导可知：

                                       当时，预测

                                       当时，预测

那么，我们将这条直线画入上图，得：

位于该直线上方的将会预测为1，位于下方的将会预测为0，这条直线我们称之为“决策边界"。

• 考虑下图所示的复杂数据集

 

在之前线性回归和多项式回归中我们曾经讨论过，对于这种复杂数据集,我们可以在原有特征的基础上创造新的特征，增加高次项进行拟合；在逻辑回归中同样适用。

假设我们的假设函数为：

                                            

并且我们假设模型参数已经通过该训练集求出(具体的求解方法之后会讲),。

由之前的推导可知：

                                       当时，预测

                                       当时，预测

通过上例我们知道，为决策边界，与之前不同，该边界时非线性边界，我们将该边界添入上图：

• 考虑更复杂的例子

假设我们的假设函数为：

                     

当我们的特征变量次数更高更复杂时，我们会得到更加复杂的决策边界，可能如下图所示：

二、逻辑回归模型

1.代价函数

如上图所示，我们现有一个分类数据集，有m个训练样本，其中输入变量是一个n+1维的向量，有n个输入特征；输出变量取值为0或1(二分类问题);假设函数如上所示。我们现在需要做的是，如何通过该训练数据集拟合出逻辑回归模型的参数。

• 我们首先回顾一下线性回归模型的代价函数：

        

       记： 

可以看到之前求解线性回归模型参数时，我们使用的代价函数为平方代价函数，那么逻辑回归的代价函数是否可以继续使用平方代价函数呢？我们先来看这样一个问题：

上图中我们绘制出两幅代价函数随模型参数的变化曲线，左图我们称之为非凸函数，很明显我们可以发现他有很多局部最小值，之前有提到过，梯度下降法只能找到局部最优解，不保证找到全局最优解，也就是说如果代价函数随参数的变化曲线是非凸函数的话，我们不能保证得到全局最小值；我们希望的是右图这种凸函数的情况，有利于我们找到全局最小值。

因此定义定价函数时，应满足其随参数的变化曲线是一个凸函数。因为逻辑回归引入sigmoid函数的缘故，我们都知道这是一个非线性函数，所以如果采用和线性回归一样的平方代价函数，是不可取的，此时会得到一个非凸函数。因此，我们要重新定义逻辑回归的代价函数，使其是凸函数，便于我们得到全局最小值。

 

• 逻辑回归代价函数

 

逻辑回归模型使用的代价函数如上所示，它是一个分段函数。

当训练样本的标签(输出变量)时，，绘制图像如下：

当,时，此时代价函数为0，说明此时的参数拟合最优；但是当时，此时代价函数，说明此时参数拟合最差，这时我们以一个最大的Cost来惩罚我们的学习算法，继续迭代求解最优的参数。

当训练样本的标签(输出变量)时，，绘制图像如下：

当,时，此时代价函数为0，说明此时的参数拟合最优；但是当时，此时代价函数，说明此时参数拟合最差，这时我们以一个最大的Cost来惩罚我们的学习算法，继续迭代求解最优的参数。

2.简化代价函数和梯度下降法

• 通过上一小节的学习，我们可以得到逻辑回归的代价函数，如下所示：

下面我们引入一个神奇的式子，把分段的代价函数合并为一个紧凑的式子：

                  

会惊喜的发现，当你把分别代入时，上式和原来的分段表示完全等价，所以之后我们会用这一个整体的式子来表示逻辑回归的代价函数（或许这就是引入log的原因）。

• 简化后的代价函数

接下来要做的，就是基于训练样本，最小化代价函数，找出最优的模型参数。

• 使用梯度下降法求解逻辑回归

接下来手动求解上述偏导项(注意第2个log中假设函数前的负号；以及sigmoid函数的求导公式；log求导就是数学中的ln求导）

代入梯度下降得(注意后少乘了一个1/m）：

你会发现他和之前线性回归得到的式子一模一样，那么二者是同一个算法吗？显然不是，虽然求导后的式子一样，但是二者的假设函数是不同的。

注意之前讲过的梯度下降法优化技巧在这里也是适用的，如特征缩放，学习率选择等，这些都可以加快收敛速度。详细内容见上一篇博客。

3.高级优化方法

在之前的讲解中，我们一直在使用梯度下降法来最小化代价函数，以此来求解最优的参数。但是当你面对一个海量的数据集，特征数目很多时，梯度下降法也许会有些局限性。本节课将介绍几种高级优化方法。

这几种算法相较于梯度下降法的优点是不需要人工选择一个合适的学习率(你可以认为这些算法内部会自动选择一个最合适的学习率),而且通常比梯度下降法速度要快；缺点就是更加复杂。

这几种算法的细节不必细究，现在你需要做的就是知道如何使用它，也不用自己写代码实现，知道如何调用软件库实现即可，具体原理可以以后慢慢研究。接下里介绍高级优化方法，如何在Matlab/Octave中使用：

在上面的这个例子中，我们定义了一个代价函数，并计算出他的梯度，下面演示如何用高级优化方法来最小化代价函数，求解最优的参数。

首先我们在Matlab中定义一个函数，该函数的参数为待求解参数，内部依次计算代价函数值，以及各个梯度值，并返回代价函数值和梯度值。

然后我们需要运行以下函数，他会调用高级优化方法中的一种来最小化代价函数求解参数，你可以把它想象为调用梯度下降法，只是不需要你手动设置学习率。

第一行可以看作是构造一种特定的数据结构，作为高级优化方法的参数，这种数据结构的参数前两项现在可以不必关心，照着写就行，后两项是设置最大的迭代次数；第二行是初始化参数为0；第三，四行是调用高级优化方法，其参数为我们之前构造的函数(前面不要忘记加@），初始化的参数，以及之前构造的数据结构，其返回值为最优的参数值以及此时的代价函数值。

这里需要注意的是，用高级优化方法求解参数，参数的维度必须大于等于2，至于一维参数的优化求解，需要自行查找其他方法。

接下来我们把这种方法推广到求解n+1维参数：

和之前求解2维一样，首先还是要定义一个函数，其参数，内部的计算以及返回值含义都与之前相同，之后调用高级优化方法的步骤也是相同的。

4.多分类问题

之前我们一直在讨论如何用逻辑回归算法求解二分类问题，本小节我们将介绍用逻辑回归算法求解多分类问题。

首先看几个多分类问题的例子：

这里提到的有邮件的自动归档，属于工作、朋友、家庭还是爱好类；医学诊断，是没病、感冒还是流感；以及天气的预测，是晴天、多云、下雨还是下雪。不同类别的标号可以从0也可以从1开始，这个无所谓。

假设我们现在有一个三分类的数据集，可视化后如下所示：

该数据集的输入变量有两个特征，输出变量有3个类别；我们接下来要做的就是基于这个训练集，训练出一个分类器(确定模型参数),来完成这个三分类，比如采用逻辑回归分类器，我们可以这么做：

把这个三分类问题看作是3个二分类问题。首先把三角看作正类，其余两类统一看作负类，定义一个逻辑回归的分类器(假设函数),通过这个训练集，利用相关优化算法，最小化代价函数，求解出模型参数，得到分类器；其余的两个2分类问题也一样。这样我们会得到三个分类器，其决策边界如右边3幅图的蓝线所示。

接下来对于一个新的输入变量，分别代入训练好的三个分类器，得到它在三个分类器中属于其正类的概率，取最大的概率，那么这个新的输入变量就属于这个类别。公式如下：

三、过拟合

1.过拟合问题

• 线性回归

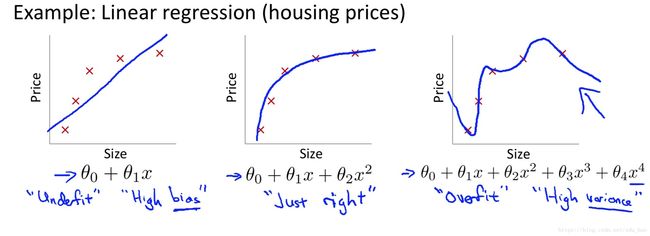
首先我们以之前讲过的线性回归的例子来说明过拟合问题，还是以房价数据集为例，输入变量只有一个特征即面积，输出变量为房价，可视化该数据集，然后分别用线性回归的不同模型来拟合，得下图：

第一张图中，我们用一次多项式来拟合训练样本，很显然这个效果是不好的，随着面积的增大，房价应该趋于平缓，因此，我们把图1中的情况称之为欠拟合，或高偏差；第二张图中，我们用二次多项式来拟合训练样本，可以看到效果刚刚好；第三张图中，我们用4次多项式来拟合训练样本，可以看到它通过了所有样本点，在训练集上效果非常好，但是模型有些过于复杂，这并不是一个好的模型，我们称之为过拟合或高方差。

过拟合：如果我们有很多特征，学习到的假设函数在训练集上拟合效果非常好，,但该模型无法泛化到新的样本数据中，无法很好的预测出新样本的房价。

泛化：假设模型能够应用到新样本的能力。

• 逻辑回归

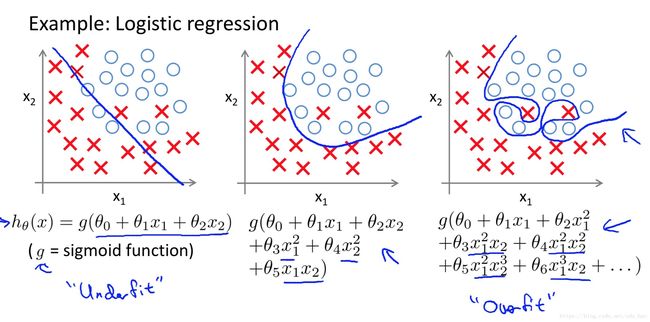
接下来我们以逻辑回归的例子来说明过拟合问题，输入变量有两个特征，输出变量为二分类，可视化该数据集，然后分别用逻辑回归的不同模型来分类，得下图：

第一张图中，拟合训练样本得到的决策边界是直线，很显然这个效果不是很好，因此，我们把图1中的情况称之为欠拟合，或高偏差；第二张图中，拟合训练样本得到一个二次的决策边界，虽然有个别训练样本分错了，但是可以看到效果算是很不错；第三张图中，拟合训练样本得到一个非常复杂的决策边界，可以看到它分对了所有样本点，在训练集上效果非常好，但是模型有些过于复杂，这并不是一个好的模型，我们称之为过拟合或高方差，泛化能力比较差。

• 如何解决过拟合

当模型的输入特征非常多，而且训练样本比较少时，非常容易出现过拟合。

目前过拟合主要的解决方法有两种：

1）减少输入特征的数量：可以人工选择一些比较重要的特征，或者使用模型特征的选择算法，自动选择一些特征(之后会讲)

2)正则化：保留所有输入特征，但减小参数的值，当我们有很多输入特征，而且每个特征都对预测输出值有一些影响时，效果会很好。

2.代价函数(正则化)

在之前的小节中，我们也提到过，如果用二次函数拟合下图所示的训练集将会得到一个不错的效果；而使用四次多项式拟合训练集时，虽然它在训练集上的拟合效果非常好，但是这个函数实际上是过拟合的，泛化能力很差。

假设我们对代价函数做一些修改，惩罚参数使其值变小。新的代价函数如上所示，它是由原来的代价函数加上两个惩罚性构成，增大两个参数对代价函数的影响。

当我们利用优化算法最小化这个代价函数求解参数时，由于惩罚项的存在，要想使代价函数整体变小，很显然要非常小(接近于0），因为惩罚项的系数为1000，比较大，对代价函数整体影响很大。

那么，最终的优化效果就是都接近于0，这样就近似等价于假设函数没有后面的两个高次项，实际上和左图的假设函数是一致的，都是2次函数，这样就可以避免过拟合，达到一个很好的效果。这就是正则化方法的思想。

 

正则化思想：使假设模型的参数的值变小，从而让假设模型更加简单，平滑，降低过拟合的风险。和上例不同的是，我们并不知道要减小哪个参数，给哪个参数添加惩罚项。实际上，在做正则化时，是对所有的参数(除)添加惩罚项.

• 线性回归加入正则化惩罚项后的代价函数：

此时的代价函数由两部分组成，第一部分使模型在训练集上的拟合效果尽可能的好；第二部分是惩罚项，它使得模型参数值减小，避免前一部分过拟合。二者做一个平衡。然后就是利用优化算法，最小化这个新的代价函数，得到最优的一组参数。图中的蓝线和红线分别代表正则化前/后的拟合效果。

• 正则化惩罚项系数

如果过大时，对参数的惩罚力度过大，此时得到的模型参数基本上是趋于0，那么假设函数,在下图的这个例子中，我们就只能得到一个水平的直线，很显然这是一个欠拟合的例子。因此，为了发挥正则化应有的效果，我们必须要选择一个合适的值。

3.线性回归中的正则化

加入正则化惩罚项的代价函数如下图所示，我们的目标是最小化这个代价函数，求解最优的模型参数：

对于线性回归模型我们讲过两种优化求参数的方法，一种是梯度下降法，另一种是正规方程法。现在让我们看一下，代价函数加入正则化惩罚项后，这两种方法有什么变化。

• 梯度下降法

由于没有惩罚项，所以单独列出来，其梯度形式和原来没有区别；由于有惩罚项，所以它们的梯度是在原来的基础上加上惩罚项产生的梯度。

接下来对的迭代形式进行整理，将合并同类项，得到下式：

式子的前一部分可以看作是先让乘以一个比1小的值，先减小一下，再减去后一部分，而后一部分就是原来不加惩罚项时，参数的梯度。

• 正规方程法

直接对加入惩罚项的新代价函数求偏导，使其值为0，求解出模型的最优参数。即：

此时得到的最优参数值为：

其中，矩阵X(m*(n+1)维)由所用训练样本的输入变量构成，向量y(m维)为所有训练样本的输出变量：

之前我们曾提到过，如果训练样本数量m小于输入特征维数n的话，是不可逆的。但是如果对正规方程使用了正则化，它不仅能够避免过拟合，而且它还能保证下图中的部分一定是可逆的，具体原因现在还不能解释：

4.逻辑回归中的正则化

首先我们写出加入正则化惩罚项的代价函数：

在逻辑回归中，我们同样讲解了两种优化方法来最小化代价函数，求解参数。一种是梯度下降法，另一种是高级优化方法。接下来分别看一下，加入惩罚项后，二者优化过程的变化：

• 梯度下降法

由于没有惩罚项，所以单独列出来，其梯度形式和原来没有区别；由于有惩罚项，所以它们的梯度是在原来的基础上加上惩罚项产生的梯度。可以看到，形式和线性回归是一样的，但是注意二者的假设函数是不同的。

• 高级优化方法

和之前一样，需要先定义一个函数，函数的参数和返回值意义均和之前没加惩罚项一致，具体内部的梯度计算公式和代价函数公式稍有不同，加上了正则化惩罚项：

之后调用高级优化方法的步骤和之前相同。

四、第三周编程实验

具体实验细节，请参照我的另一篇博客：

逻辑回归实验