PyTorch 之 神经网络 Mnist 分类任务
文章目录
- 一、Mnist 分类任务简介
- 二、Mnist 数据集的读取
- 三、 Mnist 分类任务实现
-
- 1. 标签和简单网络架构
- 2. 具体代码实现
- 四、使用 TensorDataset 和 DataLoader 简化
本文参加新星计划人工智能(Pytorch)赛道:https://bbs.csdn.net/topics/613989052
![]()
一、Mnist 分类任务简介
- 在上一篇博客当中,我们通过搭建 PyTorch 神经网络实现了气温预测,这本质上是一个回归任务。在本次博文当中,我们使用 PyTorch 做一个分类任务。
- 其实,分类任务和回归任务在本质上没有任何区别,只是说在结果上是不同的,损失函数是不同的,中间的网络架构却是大体一致的。
- 在本次的分类任务当中,我们使用的数据集是 Mnist 数据集,这个数据集大家都比较熟悉,可以在 http://yann.lecun.com/exdb/mnist/ 中获取,主要包括四个文件:
| 文件名称 | 大小 | 内容 |
|---|---|---|
| train-images-idx3-ubyte.gz | 9,681 kb | 55000 张训练集,5000 张验证集 |
| train-labels-idx1-ubyte.gz | 29 kb | 训练集图片对应的标签 |
| t10k-images-idx3-ubyte.gz | 1,611kb | 10000 张测试集 |
| t10k-labels-idx1-ubyte.gz | 5 kb | 测试集图片对应的标签 |
- 在上述在上述文件中,训练集 train 一共包含了 60000 张图像和标签,而测试集一共包含了 10000 张图像和标签。
- idx3 表示 3 维,ubyte 表示是以字节的形式进行存储的,t10k 表示 10000 张测试图片(test10000)。
- 每张图片是一个 28*28 像素点的 0 ~ 9 的灰质手写数字图片,黑底白字,图像像素值为 0 ~ 255,越大该点越白。
- 本次分类任务主要包含如下的几个部分:
- (1) 网络基本构建与训练方法,常用函数解析。
- (2) torch.nn.functional 模块。
- (3) nn.Module 模块。
二、Mnist 数据集的读取
- 对于 Mnist 数据集,我们可以通过代码编写,就可以实现自动下载。
%matplotlib inline
from pathlib import Path
import requests
DATA_PATH = Path("data")
PATH = DATA_PATH / "mnist"
PATH.mkdir(parents=True, exist_ok=True)
URL = "http://deeplearning.net/data/mnist/"
FILENAME = "mnist.pkl.gz"
- 对于我们上面定义的下载路径等等,会进行自动判断,如果该路径下没有 Minst 数据集的话,就会自动进行下载。
if not (PATH / FILENAME).exists():
content = requests.get(URL + FILENAME).content
(PATH / FILENAME).open("wb").write(content)
- 由于下载出来的数据集是压缩包的状态,因此,我们还需要对其进行解压,具体的代码详见下面。
import pickle
import gzip
with gzip.open((PATH / FILENAME).as_posix(), "rb") as f:
((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding="latin-1")
- 在上述工作准备完成后,我们可以先查看一个数据,观察他的特征。
from matplotlib import pyplot
import numpy as np
pyplot.imshow(x_train[0].reshape((28, 28)), cmap="gray")
print(x_train.shape)
#(50000, 784)
- 在此处,我们查看的训练集当中的第一个数据,大小重构为 (28,28,1),表示长是 28,宽是 28,颜色通道是 1(黑白图就只有一个颜色通道),颜色设置为灰色。在查看第一个数据的同时,我们也输出整个训练集的数据大小,其中,(50000, 784) 中的 50000 表示训练集一共有 50000 个数据样本,784 表示训练集中每个样本有 784 个像素点(可以理解成 784 个特征)。
三、 Mnist 分类任务实现
1. 标签和简单网络架构
- 在分类任务当中,标签的设计是有所不同的。
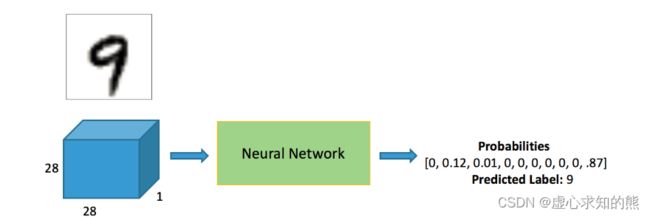
- 很多人认为预测出来的 9,具体指的是 0,1,2,3,4,5,6,7,8,9 当中的具体哪一个,但实际上并不是这样的,他也是一个 One-Hot 的编码,他预测的出来的不是一个具体的数值,而是十个概率,就是当前这个输入属于 0-9 这十个数字的概率是多少。
- 以上图为例,该输入属于 0 的概率就是 0,属于 1 的概率就是 12%,属于 9 的概率就是 87%,属于 9 的概率最高,因此,该输入的输出就是 9。
- 对于这个网络架构,由于我们的每个数据样本都有 784 个像素点,中间进行特征提取,得到一定数量的特征,最终得到 10 个输出,通过 Softmax 层得到是个概率。
2. 具体代码实现
- 需要注意的是,我们需要先将数据转换成 tensor 才能参与后续建模训练。
- 这里的数据包括 x_train, y_train, x_valid, y_valid 四种,对于他们的含义,我们可以这样理解:
- (1) x_train 包括所有自变量,这些变量将用于训练模型。
- (2) y_train 是指因变量,需要此模型进行预测,其中包括针对自变量的类别标签,我们需要在训练/拟合模型时指定我们的因变量。
- (3) x_valid 也就是 x_test,这些自变量将不会在训练阶段使用,并将用于进行预测,以测试模型的准确性。
- (4) y_valid 也就是 y_test,此数据具有测试数据的类别标签,这些标签将用于测试实际类别和预测类别之间的准确性。
import torch
x_train, y_train, x_valid, y_valid = map(
torch.tensor, (x_train, y_train, x_valid, y_valid)
)
n, c = x_train.shape
x_train, x_train.shape, y_train.min(), y_train.max()
print(x_train, y_train)
print(x_train.shape)
print(y_train.min(), y_train.max())
#tensor([[0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.],
# ...,
# [0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.],
# [0., 0., 0., ..., 0., 0., 0.]]) tensor([5, 0, 4, ..., 8, 4, 8])
#torch.Size([50000, 784])
#tensor(0) tensor(9)
- 在模型训练的过程中,大家经常会看到 nn.Module 和 nn.functional。那什么时候使用 nn.Module,什么时候使用 nn.functional 呢?
- 一般情况下,如果模型有可学习的参数,最好用 nn.Module,其他情况 nn.functional 相对更简单一些。
- 我们先导入需要的模块包。
import torch.nn.functional as F
loss_func = F.cross_entropy
def model(xb):
return xb.mm(weights) + bias
- 然后进行参数的设定。
bs = 64
xb = x_train[0:bs] # a mini-batch from x
yb = y_train[0:bs]
weights = torch.randn([784, 10], dtype = torch.float, requires_grad = True)
bs = 64
bias = torch.zeros(10, requires_grad=True)
print(loss_func(model(xb), yb))
#tensor(10.7988, grad_fn=)
- 我们也创建一个 model 来更简化代码。
- 在这中间必须继承 nn.Module 且在其构造函数中需调用 nn.Module 的构造函数,无需写反向传播函数,nn.Module 能够利用 autograd 自动实现反向传播,Module 中的可学习参数可以通过 named_parameters() 或者 parameters() 返回迭代器。
from torch import nn
class Mnist_NN(nn.Module):
def __init__(self):
super().__init__()
self.hidden1 = nn.Linear(784, 128) #隐藏层1:784*128
self.hidden2 = nn.Linear(128, 256) #隐藏层2:128*256
self.out = nn.Linear(256, 10) #输出层,256*10
def forward(self, x):
x = F.relu(self.hidden1(x))
x = F.relu(self.hidden2(x))
x = self.out(x)
return x
net = Mnist_NN()
print(net)
#Mnist_NN(
# (hidden1): Linear(in_features=784, out_features=128, bias=True)
# (hidden2): Linear(in_features=128, out_features=256, bias=True)
# (out): Linear(in_features=256, out_features=10, bias=True)
#)
- 我们可以打印定义好名字里的权重和偏置项,首先打印名字,然后打印参数,最后打印参数的维度。
for name, parameter in net.named_parameters():
print(name, parameter,parameter.size())
#hidden1.weight Parameter containing:
#tensor([[ 0.0018, 0.0218, 0.0036, ..., -0.0286, -0.0166, 0.0089],
# [-0.0349, 0.0268, 0.0328, ..., 0.0263, 0.0200, -0.0137],
# [ 0.0061, 0.0060, -0.0351, ..., 0.0130, -0.0085, 0.0073],
# ...,
# [-0.0231, 0.0195, -0.0205, ..., -0.0207, -0.0103, -0.0223],
# [-0.0299, 0.0305, 0.0098, ..., 0.0184, -0.0247, -0.0207],
# [-0.0306, -0.0252, -0.0341, ..., 0.0136, -0.0285, 0.0057]],
# requires_grad=True) torch.Size([128, 784])
#hidden1.bias Parameter containing:
#tensor([ 0.0072, -0.0269, -0.0320, -0.0162, 0.0102, 0.0189, -0.0118, -0.0063,
# -0.0277, 0.0349, 0.0267, -0.0035, 0.0127, -0.0152, -0.0070, 0.0228,
# -0.0029, 0.0049, 0.0072, 0.0002, -0.0356, 0.0097, -0.0003, -0.0223,
# -0.0028, -0.0120, -0.0060, -0.0063, 0.0237, 0.0142, 0.0044, -0.0005,
# 0.0349, -0.0132, 0.0138, -0.0295, -0.0299, 0.0074, 0.0231, 0.0292,
# -0.0178, 0.0046, 0.0043, -0.0195, 0.0175, -0.0069, 0.0228, 0.0169,
# 0.0339, 0.0245, -0.0326, -0.0260, -0.0029, 0.0028, 0.0322, -0.0209,
# -0.0287, 0.0195, 0.0188, 0.0261, 0.0148, -0.0195, -0.0094, -0.0294,
# -0.0209, -0.0142, 0.0131, 0.0273, 0.0017, 0.0219, 0.0187, 0.0161,
# 0.0203, 0.0332, 0.0225, 0.0154, 0.0169, -0.0346, -0.0114, 0.0277,
# 0.0292, -0.0164, 0.0001, -0.0299, -0.0076, -0.0128, -0.0076, -0.0080,
# -0.0209, -0.0194, -0.0143, 0.0292, -0.0316, -0.0188, -0.0052, 0.0013,
# -0.0247, 0.0352, -0.0253, -0.0306, 0.0035, -0.0253, 0.0167, -0.0260,
# -0.0179, -0.0342, 0.0033, -0.0287, -0.0272, 0.0238, 0.0323, 0.0108,
# 0.0097, 0.0219, 0.0111, 0.0208, -0.0279, 0.0324, -0.0325, -0.0166,
# -0.0010, -0.0007, 0.0298, 0.0329, 0.0012, -0.0073, -0.0010, 0.0057],
# requires_grad=True) torch.Size([128])
#hidden2.weight Parameter containing:
#tensor([[-0.0383, -0.0649, 0.0665, ..., -0.0312, 0.0394, -0.0801],
# [-0.0189, -0.0342, 0.0431, ..., -0.0321, 0.0072, 0.0367],
# [ 0.0289, 0.0780, 0.0496, ..., 0.0018, -0.0604, -0.0156],
# ...,
# [-0.0360, 0.0394, -0.0615, ..., 0.0233, -0.0536, -0.0266],
# [ 0.0416, 0.0082, -0.0345, ..., 0.0808, -0.0308, -0.0403],
# [-0.0477, 0.0136, -0.0408, ..., 0.0180, -0.0316, -0.0782]],
# requires_grad=True) torch.Size([256, 128])
#hidden2.bias Parameter containing:
#tensor([-0.0694, -0.0363, -0.0178, 0.0206, -0.0875, -0.0876, -0.0369, -0.0386,
# 0.0642, -0.0738, -0.0017, -0.0243, -0.0054, 0.0757, -0.0254, 0.0050,
# 0.0519, -0.0695, 0.0318, -0.0042, -0.0189, -0.0263, -0.0627, -0.0691,
# 0.0713, -0.0696, -0.0672, 0.0297, 0.0102, 0.0040, 0.0830, 0.0214,
# 0.0714, 0.0327, -0.0582, -0.0354, 0.0621, 0.0475, 0.0490, 0.0331,
# -0.0111, -0.0469, -0.0695, -0.0062, -0.0432, -0.0132, -0.0856, -0.0219,
# -0.0185, -0.0517, 0.0017, -0.0788, -0.0403, 0.0039, 0.0544, -0.0496,
# 0.0588, -0.0068, 0.0496, 0.0588, -0.0100, 0.0731, 0.0071, -0.0155,
# -0.0872, -0.0504, 0.0499, 0.0628, -0.0057, 0.0530, -0.0518, -0.0049,
# 0.0767, 0.0743, 0.0748, -0.0438, 0.0235, -0.0809, 0.0140, -0.0374,
# 0.0615, -0.0177, 0.0061, -0.0013, -0.0138, -0.0750, -0.0550, 0.0732,
# 0.0050, 0.0778, 0.0415, 0.0487, 0.0522, 0.0867, -0.0255, -0.0264,
# 0.0829, 0.0599, 0.0194, 0.0831, -0.0562, 0.0487, -0.0411, 0.0237,
# 0.0347, -0.0194, -0.0560, -0.0562, -0.0076, 0.0459, -0.0477, 0.0345,
# -0.0575, -0.0005, 0.0174, 0.0855, -0.0257, -0.0279, -0.0348, -0.0114,
# -0.0823, -0.0075, -0.0524, 0.0331, 0.0387, -0.0575, 0.0068, -0.0590,
# -0.0101, -0.0880, -0.0375, 0.0033, -0.0172, -0.0641, -0.0797, 0.0407,
# 0.0741, -0.0041, -0.0608, 0.0672, -0.0464, -0.0716, -0.0191, -0.0645,
# 0.0397, 0.0013, 0.0063, 0.0370, 0.0475, -0.0535, 0.0721, -0.0431,
# 0.0053, -0.0568, -0.0228, -0.0260, -0.0784, -0.0148, 0.0229, -0.0095,
# -0.0040, 0.0025, 0.0781, 0.0140, -0.0561, 0.0384, -0.0011, -0.0366,
# 0.0345, 0.0015, 0.0294, -0.0734, -0.0852, -0.0015, -0.0747, -0.0100,
# 0.0801, -0.0739, 0.0611, 0.0536, 0.0298, -0.0097, 0.0017, -0.0398,
# 0.0076, -0.0759, -0.0293, 0.0344, -0.0463, -0.0270, 0.0447, 0.0814,
# -0.0193, -0.0559, 0.0160, 0.0216, -0.0346, 0.0316, 0.0881, -0.0652,
# -0.0169, 0.0117, -0.0107, -0.0754, -0.0231, -0.0291, 0.0210, 0.0427,
# 0.0418, 0.0040, 0.0762, 0.0645, -0.0368, -0.0229, -0.0569, -0.0881,
# -0.0660, 0.0297, 0.0433, -0.0777, 0.0212, -0.0601, 0.0795, -0.0511,
# -0.0634, 0.0720, 0.0016, 0.0693, -0.0547, -0.0652, -0.0480, 0.0759,
# 0.0194, -0.0328, -0.0211, -0.0025, -0.0055, -0.0157, 0.0817, 0.0030,
# 0.0310, -0.0735, 0.0160, -0.0368, 0.0528, -0.0675, -0.0083, -0.0427,
# -0.0872, 0.0699, 0.0795, -0.0738, -0.0639, 0.0350, 0.0114, 0.0303],
# requires_grad=True) torch.Size([256])
#out.weight Parameter containing:
#tensor([[ 0.0232, -0.0571, 0.0439, ..., -0.0417, -0.0237, 0.0183],
# [ 0.0210, 0.0607, 0.0277, ..., -0.0015, 0.0571, 0.0502],
# [ 0.0297, -0.0393, 0.0616, ..., 0.0131, -0.0163, -0.0239],
# ...,
# [ 0.0416, 0.0309, -0.0441, ..., -0.0493, 0.0284, -0.0230],
# [ 0.0404, -0.0564, 0.0442, ..., -0.0271, -0.0526, -0.0554],
# [-0.0404, -0.0049, -0.0256, ..., -0.0262, -0.0130, 0.0057]],
# requires_grad=True) torch.Size([10, 256])
#out.bias Parameter containing:
#tensor([-0.0536, 0.0007, 0.0227, -0.0072, -0.0168, -0.0125, -0.0207, -0.0558,
# 0.0579, -0.0439], requires_grad=True) torch.Size([10])
四、使用 TensorDataset 和 DataLoader 简化
- 自己构建数据集,使用 batch 取数据会略显麻烦,因此,我们可以使用 TensorDataset 和 DataLoader 这两个模块进行简化。
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
train_ds = TensorDataset(x_train, y_train)
train_dl = DataLoader(train_ds, batch_size=bs, shuffle=True)
valid_ds = TensorDataset(x_valid, y_valid)
valid_dl = DataLoader(valid_ds, batch_size=bs * 2)
def get_data(train_ds, valid_ds, bs):
return (
DataLoader(train_ds, batch_size=bs, shuffle=True),
DataLoader(valid_ds, batch_size=bs * 2),
)
- 一般在训练模型时加上 model.train(),这样会正常使用 Batch Normalization 和 Dropout。
- 测试的时候一般选择 model.eval(),这样就不会使用 Batch Normalization 和 Dropout。
import numpy as np
def fit(steps, model, loss_func, opt, train_dl, valid_dl):
for step in range(steps):
model.train()
for xb, yb in train_dl:
loss_batch(model, loss_func, xb, yb, opt)
model.eval()
with torch.no_grad():
losses, nums = zip(
*[loss_batch(model, loss_func, xb, yb) for xb, yb in valid_dl]
)
val_loss = np.sum(np.multiply(losses, nums)) / np.sum(nums)
print('当前step:'+str(step), '验证集损失:'+str(val_loss))
from torch import optim
def get_model():
model = Mnist_NN()
return model, optim.SGD(model.parameters(), lr=0.001)
def loss_batch(model, loss_func, xb, yb, opt=None):
loss = loss_func(model(xb), yb)
if opt is not None:
loss.backward()
opt.step()
opt.zero_grad()
return loss.item(), len(xb)
- 我们也可以像上篇博文一样,使用三行代码进行解决。
train_dl, valid_dl = get_data(train_ds, valid_ds, bs)
model, opt = get_model()
fit(25, model, loss_func, opt, train_dl, valid_dl)
#当前step:0 验证集损失:2.2796445930480957
#当前step:1 验证集损失:2.2440698066711424
#当前step:2 验证集损失:2.1889826164245605
#当前step:3 验证集损失:2.0985311767578123
#当前step:4 验证集损失:1.9517273582458496
#当前step:5 验证集损失:1.7341805934906005
#当前step:6 验证集损失:1.4719875366210937
#当前step:7 验证集损失:1.2273896869659424
#当前step:8 验证集损失:1.0362271406173706
#当前step:9 验证集损失:0.8963696184158325
#当前step:10 验证集损失:0.7927186088562012
#当前step:11 验证集损失:0.7141492074012756
#当前step:12 验证集损失:0.6529350900650024
#当前step:13 验证集损失:0.60417300491333
#当前step:14 验证集损失:0.5643046331882476
#当前step:15 验证集损失:0.5317994566917419
##当前step:16 验证集损失:0.5047958114624024
#当前step:17 验证集损失:0.4813900615692139
#当前step:18 验证集损失:0.4618900228500366
#当前step:19 验证集损失:0.4443243554592133
#当前step:20 验证集损失:0.4297310716629028
#当前step:21 验证集损失:0.416976597738266
#当前step:22 验证集损失:0.406348459148407
#当前step:23 验证集损失:0.3963301926612854
#当前step:24 验证集损失:0.38733808159828187