【算法】通俗易懂的PID算法

初识PID

PID算法是连续系统中技术最为成熟、应用最为广泛的一种控制算法。该控制算法出现于20世纪30至40年代，PID 控制器以各种形式使用超过了 1 世纪，广泛应用在机械设备、气动设备 和电子设备。在工业应用中PID及其衍生算法是应用最广泛的算法之一，是当之无愧的万能算法

PID简介

Proportional（比例）、Integral（积分）、Differential（微分）的缩写。顾名思义，PID控制算法是结合比例、积分和微分三种环节于一体的控制算法


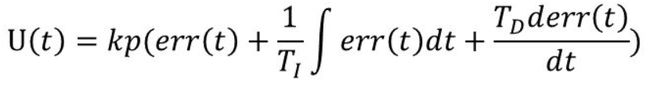
U(t)：控制器的输出量
kp：比例系数
Ti:积分系数
Td:微分系数
err(t)：误差

PID分为位置式PID和增量式PID

位置式PID：

举一个究极经典的例子：水箱储水

比例控制：

一个水箱，我现在希望水箱的水位永远维持在1米
目前的水位是0.2米，我设P=0.5，此时误差err=（1-0.2）=0.8

t = 1：
U = P * err = 0.5 * 0.8 = 0.4
此时输出量为0.4，即水箱水位上涨0.4米，即此时水位0.6米，此时误差err=（1-0.6）=0.4

t = 2：
U = P * err = 0.5 * 0.4 = 0.2
此时输出量为0.2，即水箱水位上涨0.2米，即此时水位0.8米

P * err（比例项）

以此类推，最终水位会接近极限1米，根据P取值不同，系统最后都会达到1米
只不过P大了到达的快，P小了到达的慢一些,这就是最简单的比例控制

积分控制：

但但但但但是，纯比例控制是极其理想的情况，如果我每次加水都会漏0.1米高度的水，还是同样的目前的水位是0.2米，我设P=0.5，此时误差err=（1-0.2）=0.8

t = 1：
U = P * err = 0.5 * 0.8 = 0.4
此时输出量为0.4，即水箱水位上涨0.4米，再漏0.1米水位，即此时水位0.5米，此时误差err=（1-0.5）=0.5

t = 2：
U = P * err = 0.5 * 0.5 = 0.25
此时输出量为0.25，即水箱水位上涨0.25米，再漏0.1米水位，即此时水位0.65米，此时误差err=（1-0.65）=0.35

t = 3：
U = P * err = 0.5 * 0.35 ≈ 0.17
此时输出量为0.17，即水箱水位上涨0.17米，再漏0.1米水位，即此时水位0.72米

以此类推…当水位接近于0.8米的时候，err = 0.2 ，U = 0.5 * 0.2 = 0.1 , 输出量于漏水量一致的时候，水位便不再继续增加，这就是静态误差
静态误差无可避免，只能减小。例如运动物体的摩擦阻力，灯泡发光产生的热能等等…

所以此时引入积分项 I
何为积分？ 数学中对离散的量进行积分就是累加
∫err = 0.8 + 0.4 = 1.2 （假如只用两次就达到1米）

U = P * err + I ∗ ∫ error （比例+积分）
I ∗ ∫ error （积分项）

当水位为0.8米不动了的时候，且 I 取一个合适的值时，对前面的误差进行积分累加，积分项就可以打破这个“僵持”的局面，即 U > 0.1 ,水位会逐渐增加，最终到达1米的水位。把过去的误差纠正

微分控制：

当P取的过大时，加水非常快，快接近1米的时候，如果不放缓速度，那么很有可能溢出1米的水位，此时我们需要回调一下接近速度

何为微分？数学中对离散的量进行微分就是对error 做差值

U = P * err(t) + I ∗ ∫ error + D ∗ ( err(t) − err(t−1) ) （比例+积分+微分）
D ∗ ( err(t) − err(t−1) ) （微分项）

水位在接近1米的变化中，err误差是越来越小的，所以微分项是越来越小直至变成负数。当D取合适的值时，对快接近一米时候的水位变化进行了有效缓冲，防止过度溢出1米水位
减小控制过程的震荡

C语言代码实现位置式PID：

int OUT,P_OUT,I_OUT,D_OUT,Error,Last_Error; //总输出、P输出、I输出、D输出、本次误差、上次误差
float P = 100.0 ; //随便写的值 
float I = 100.0 ;
float D = 100.0 ;
int Target_value = 500 ; //希望系统达到的值 
int value ;  //系统当前的值

void PID
{
	Error = Target_value - value ;   //计算当前误差 
	P_OUT = P * Error ;              //比例项 
	I_OUT += I * Error ;             //积分项 
	D_OUT = D * (Error - Last_Error) ;    //微分项 
	OUT = P_OUT + I_OUT + D_OUT ;     //各项相加计算输出值 
	Last_Error = Error               //本次误差赋给上次误差 
} 

增量式PID：

比例P : e(k)-e(k-1) 这次误差-上次误差

积分I : e(i) 误差

微分D : e(k) - 2e(k-1)+e(k-2) 这次误差-2*上次误差+上上次误差

此公式可以看出，一旦确定了 Kp、Ki 、Kd，使用前后三次测量值的偏差， 即可由公式求出输出量增量，而不是对应与实际位置的偏差 ，也就是说不存在静态误差，与系统的实时运行状态及增量密切相关

C语言代码实现增量式PID：

int OUT,P_OUT,I_OUT,D_OUT,Error,Last_Error,Last_Error2; //总输出、P输出、I输出、D输出、本次误差、上次误差、上上次误差 
float P = 100.0 ; //随便写的值 
float I = 100.0 ;
float D = 100.0 ;
int Target_value = 500 ; //希望系统达到的值 
int value ;  //系统当前的值

void PID
{
	Error = Target_value - value ;         //计算当前误差 
	P_OUT = P * (Error - Last_Error) ;                    //比例项 
	I_OUT += I * Error ;    //积分项 
	D_OUT = D * (Error - 2*Last_Error + Last_Error2) ;     //微分项 
	OUT = Last_OUT + P_OUT + I_OUT + D_OUT ;     //各项相加计算输出值 
	
	Last_Error = Error ;         //本次误差赋给上次误差 
} 
 

总结

位置式PID：

• 通过目标值对当前值的误差比较进行公式运算，使其不断输出达到目标值
• 每次输出均与过去的状态有关，计算时要对误差进行累加，运算工作量大
• 非递推式算法，在执行机构不带积分部件的对象中可以很好应用

增量式PID：

• 增量的确定仅与最近几次偏差采样值有关，容易通过加权处理获得比较好的控制效果
• 误动作时影响小，高强度干扰时冲击小，便于实现无扰动切换
• 积分截断效应大，有稳态误差