栈和队列经典OJ题
栈和队列经典OJ题
- 1. LeetCode第225题---用队列实现栈
- 2. LeetCode第232题---用栈实现队列
- 3. LeetCode第20题---有效的括号
- 4. LeetCode第150题---逆波兰表达式
- 5. LeetCode第155题---最小栈
- 6. 滑动窗口系列题
-
- 6.1 剑指offer59题---队列的最大值I
- 6.2 剑指offer48题---最长不含重复字符的子字符串
- 6.3 LeetCode209题---长度最小的子数组
- 6.4 LeetCode76题---最小覆盖子串(重点)
- 6.5 LeetCode567题---字符串的排列
- 6.6 LeetCode438题---找到字符串中所有字母异位词
- 7. 牛客网剑指offer21题---栈的压入、弹出序列
1. LeetCode第225题—用队列实现栈
链接: https://leetcode-cn.com/problems/implement-stack-using-queues/

题解:用队列实现栈,其中只需要一个队列,核心在于想要队列是先入先出,而战则是后进的先出,所以要在push()这个接口处下功夫思考,在我插入的时候,我把原先的数据都拿出来在重新插入一次,这样此时队列头部的值就是最后一个入队的元素,就满足了栈的后进先出的原则。
class MyStack {
public:
MyStack() {
}
void push(int x) {
int size = q.size();
q.push(x);
while(size--)
{
int tmp = q.front();
q.pop();
q.push(tmp);
}
}
int pop() {
int popVal = q.front();
q.pop();
return popVal;
}
int top() {
return q.front();
}
bool empty() {
return q.empty();
}
//使用队列来实现栈,只需要一个队列即可
private:
queue<int> q;
};
2. LeetCode第232题—用栈实现队列
链接: https://leetcode-cn.com/problems/implement-queue-using-stacks/

st1就只负责入数据,st2负责将st1里面的元素进行颠倒以达到队列的性质
class MyQueue {
private:
stack<int> st1;
stack<int> st2;
public:
MyQueue() {
}
//st1只负责入数据,st2负责将st1里面的元素进行颠倒以达到队列的性质
void push(int x) {
st1.push(x);
}
int pop() {
int val;
while(!st2.empty())
{
val = st2.top();
st2.pop();
return val;
}
while(!st1.empty())
{
val = st1.top();
st1.pop();
st2.push(val);
}
int TopVal = st2.top();
st2.pop();
return TopVal;
}
int peek() {
int val;
while(!st2.empty())
{
return st2.top();
}
while(!st1.empty())
{
val = st1.top();
st1.pop();
st2.push(val);
}
return st2.top();
}
bool empty() {
return st1.empty() && st2.empty();
}
};
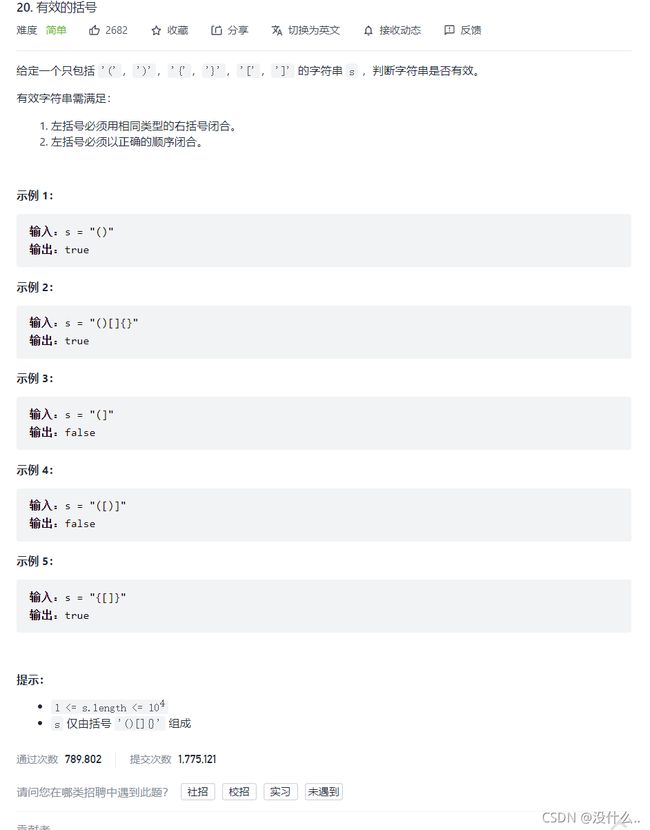
3. LeetCode第20题—有效的括号
链接: https://leetcode-cn.com/problems/valid-parentheses/
class Solution {
public:
//这道题就是典型的使用栈来解决的问题的,如果我们天真的就是去数左半边括号的数量然后再去数右半边括号的数量,这样的做法是不正确的,因为你看示例4就会发现
//真正的做法是遇见左括号就入栈,当遇见右括号的时候就进行出栈,看是否能够进行匹配
bool isValid(string s) {
stack<char> st;
for(int i = 0;i<s.size();++i)
{
if(s[i] == '(' || s[i] == '[' || s[i] == '{')
{
st.push(s[i]);
}
else
{
//[]]]
if(st.empty() == true)
return false;
//走到这里说明遇见的是右括号,那么就取栈顶的看看是否匹配
char top = st.top();
if(s[i] == ')' && top != '(')
return false;
if(s[i] == ']' && top != '[')
return false;
if(s[i] == '}' && top != '{')
return false;
st.pop();
}
}
//跳出循环的可能[[[]
if(!st.empty())
return false;
return true;
}
};
4. LeetCode第150题—逆波兰表达式
链接: https://leetcode-cn.com/problems/evaluate-reverse-polish-notation/submissions/

class Solution {
//我们仔细的审查这个逆波兰表达式就会发现
//其实我们想要操作数入栈,一旦遇见操作符我们就从栈里面把操作数拿出来,且第一个栈顶元素是右操作数,第二个是左操作数,然后我们计算的结果还是操作数,所以在入栈继续下去
public:
int evalRPN(vector<string>& tokens) {
//遇见不同的操作符,执行不同的函数
map<string,function<int(int,int)>> OpCountMap =
{
{"+",[](int x,int y)->int{return x + y;}},
{"-",[](int x,int y)->int{return x - y;}},
{"*",[](int x,int y)->int{return x * y;}},
{"/",[](int x,int y)->int{return x / y;}}
};
stack<int> st;
for(auto& str : tokens)
{
//这里要分为操作符和操作数的概念
if(str == "+" || str == "-" || str == "*" || str == "/")
{
int right = st.top();
st.pop();
int left = st.top();
st.pop();
st.push(OpCountMap[str](left,right));
}
else
{
//c++11所提供的的接口 stoi字符串转整数 还有to_string整数转字符串接口,很好用
st.push(stoi(str));
}
}
return st.top();//最后的结果还会再一次入栈,所以最终返回栈里面的top()就好
}
};
5. LeetCode第155题—最小栈
链接: https://leetcode-cn.com/problems/min-stack/

一个栈就具有正常的push()和pop(),还有一个叫做最小栈,这个栈专门用来存储插入的过程中,遇见的比之前都小的值。(从事列-2,0,-3就可以理解这段话)
class MinStack {
public:
MinStack() {
}
void push(int val) {
st.push(val);
if(min_st.empty() || val <= min_st.top())
min_st.push(val);
}
void pop() {
int top = st.top();
st.pop();
if(min_st.top() == top)
min_st.pop();
}
int top() {
return st.top();
}
int getMin() {
return min_st.top();
}
stack<int> st;
stack<int> min_st;
};
6. 滑动窗口系列题
6.1 剑指offer59题—队列的最大值I
链接:https://leetcode-cn.com/problems/dui-lie-de-zui-da-zhi-lcof/


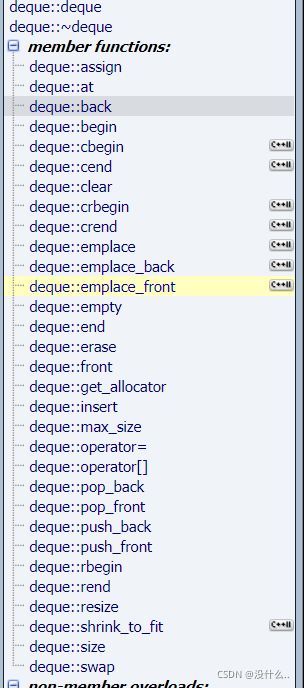
之所以使用双端队列的原因就在于,要使用一种能够既能从头部出数据的,也可以从尾部出数据的结构,所以选择双端队列是最好的,且这里还需要再附上deque的基本使用方法,害怕日后忘记了。
class MaxQueue {
public:
MaxQueue() {
}
int max_value() {
return deq.empty() ? -1:deq.front();
}
//
void push_back(int value) {
que.push(value);
while(!deq.empty() && deq.back() < value)
{
deq.pop_back();
}
//要保持deq是用来维持单调递减的队列,且第一个是最大值
deq.push_back(value);
}
int pop_front() {
if(que.empty())
return -1;
int top = que.front();
if(top == deq.front())
{
deq.pop_front();
}
que.pop();
return top;
}
private:
//需要借助两个队列
queue<int> que;
//需要一个既能够从前出,也能够从后出的一种数据结构
deque<int> deq;
};
6.2 剑指offer48题—最长不含重复字符的子字符串
LeetCode题目链接:https://leetcode-cn.com/problems/zui-chang-bu-han-zhong-fu-zi-fu-de-zi-zi-fu-chuan-lcof/

解题思路:这道题为了最大程度上减少时间复杂度的问题,我们就可以选择滑动窗口的方式来解决这道题,当然这道题也可以使用动态规划的解法,但是并不好理解。所以我么这道题最好的方式就是使用滑动窗口。
简单点说:①需要定义一个unordered_map用来记录当前元素和其下标,但是这里还有一个问题就是
②定义了一个滑动窗口,其中start表示窗口左边的下标,i表示的就是右边的下标,那么在这个窗口里面的就是我们要找的最长且无重复的子串,如果没有重复的那么这个窗口就会向右扩大,如果有重复的,那么就要找到前面重复的那个字符的下标,然后跳过该字符前面的所有字符,也就是缩小窗口的大小
③但是这道题最需要注意的一点就是这个start的计算,因为是由可能会出现倒退的情况的,所以要使用一个max
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<char,int> hashmap; //每一个字符对应的下标位置
int start = 0,Maxlong = 0;//这两个变量定义的是窗口的左右区间
//当字符没有出现的时候,那么我们就将pos往右移动,扩大滑动窗口的大小,但是如果在前面出现了
//那么我们就应该将其start右移,来缩小区间的大小
for(int i = 0;i<s.size();++i)
{
if(hashmap.find(s[i]) != hashmap.end())
{
//说明在里面找到了重复的字符,那么我们就应该调整区间的大小,将左区间右移
//这个start的位置应该怎么调整呢?
//这道题这个点才是最难的
//abba这个测试用例就是最好的方式
start = std::max(start,hashmap[s[i]]+1);
//我这样子写为啥就是错的呢?需要好好思考一下
//因为需要保证的是[left,right]没有重复值。而你的left如果不取最大值的话,是有可能往前退,就无法保证这个条件了。比如abba , 到第二个a的时候,这时候上一轮的第二个b完成,此时left=2 ,而a上一次出现的地方是0。如果你直接left = hashMap[ch] + 1 ,此时 left = 1 ,范围为[left,right] = [1,3] 而此时[1,2] = bb ,b已经重复了。
//start = hashmap[s[i]] + 1;
}
hashmap[s[i]] = i;
Maxlong = std::max(Maxlong,i-start+1);//这个就是当前最长无重复字符的长度
}
return Maxlong;
}
};
解法②:这道题使用了一个unordered_set,来记录每个字符,这里最大的好处就是我们直接采用删除的方式,那么我们就不需要迷惑上面一种解法当中的start的解法需要去max值的问题。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_set<char> hashset; //每一个字符对应的下标位置
int start = 0,Maxlong = 0;//这两个变量定义的是窗口的左右区间
//当字符没有出现的时候,那么我们就将pos往右移动,扩大滑动窗口的大小,但是如果在前面出现了
//那么我们就应该将其start右移,来缩小区间的大小
for(int i = 0;i<s.size();++i)
{
while(hashset.find(s[i]) != hashset.end())
{
hashset.erase(s[start]);
start++;
}
hashset.insert(s[i]);
Maxlong = std::max(Maxlong,i-start+1);//这个就是当前最长无重复字符的长度
}
return Maxlong;
}
};
6.3 LeetCode209题—长度最小的子数组
LeetCode题目链接:https://leetcode-cn.com/problems/minimum-size-subarray-sum/

class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
//这题我们使用滑动窗口的方式来做题
int start = 0; //窗口的起始
int result = INT_MAX;
int sum = 0;//这个求的是在滑动窗口里面值的大小
for(int i = 0;i<nums.size();++i)
{
sum += nums[i];
while(sum >= target)
{
//直到sum>= target的时候
result = std::min(result,i-start+1);
sum -= nums[start++];//此时需要调整左边的窗口进行移动
}
}
//有这个判断是因为,如果全部的都相加也没有超过我们想要的target,那么就应该返回0
return result == INT_MAX? 0:result;
}
};
6.4 LeetCode76题—最小覆盖子串(重点)
LeetCode题目链接:https://leetcode-cn.com/problems/minimum-window-substring/

我发现这道题有一个点,我依旧还没有想通,需要过几天重新回来继续看
class Solution {
public:
string minWindow(string s, string t) {
unordered_map<char, int> map;
for (auto c : t) map[c]++;
int left = 0, cnt = 0, maxlen = s.size() + 1, start = left;
for (int i = 0; i < s.size(); ++i) {
if (--map[s[i]] >= 0) ++cnt;
while(cnt == t.size()) {
//当找到一组可行解的时候,剩下的操作就是要向左收缩这个可行解,一边寻找到最优解
if (maxlen > i - left + 1) {
maxlen = i - left + 1;
start = left;
}
if(++map[s[left]] > 0) cnt--;
left++;
}
}
return maxlen == s.size() + 1 ? "" : s.substr(start, maxlen);
}
};
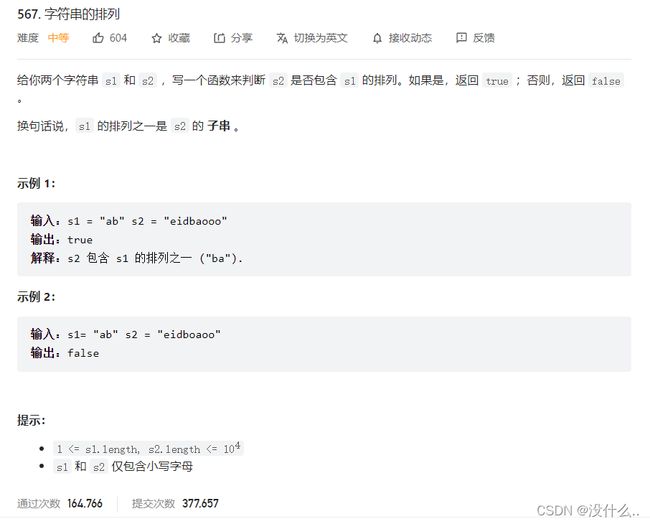
6.5 LeetCode567题—字符串的排列
LeetCode题目链接:https://leetcode-cn.com/problems/permutation-in-string/
class Solution {
public:
bool checkInclusion(string s1, string s2) {
vector<int> count(26);
for (auto& e : s1)
count[e-'a']++;
for (int l = 0,r = 0; r < s2.size(); r++)
{
--count[s2[r]-'a'];
//如果此时小于0,说明这个字符是没有出现的在s1中,需要重新的调整窗口
//就是调整左边的窗口,首先就是把原先的那个数从窗口中移出去
while (count[s2[r]-'a'] < 0)
count[s2[l++]-'a']++;
if (r-l + 1 == s1.size())
return true;
}
return false;
}
};
6.6 LeetCode438题—找到字符串中所有字母异位词
LeetCode题目链接:https://leetcode-cn.com/problems/find-all-anagrams-in-a-string/

class Solution {
public:
vector<int> findAnagrams(string s, string p) {
vector<int> vs(26,0);
vector<int> vp(26,0);
//统计字符p里面各个字符出现的次数
for(char& e : p)
vp[e-'a']++;
vector<int> result;
//定义一个滑动窗口
for(int left = 0,right = 0;right<s.size();++right)
{
vs[s[right]-'a']++;
//这一段while代码还是理解的不对劲
while(vs[s[right]-'a'] > vp[s[right]-'a'])
{
//此时就应该调整窗口的大小
//有两种可能一种就是这个字符在s中出现了,但是在p中没有出现
//还有一种可能就是这个字符在s中出现的次数超过了p中出现的次数
vs[s[left]-'a']--;
left++;
}
if(right-left+1 == p.size())
result.push_back(left);
}
return result;
}
};
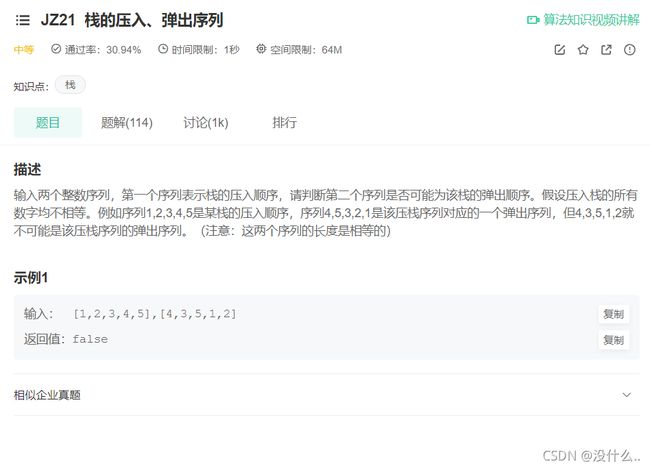
7. 牛客网剑指offer21题—栈的压入、弹出序列
链接: https://www.nowcoder.com/practice/d77d11405cc7470d82554cb392585106?tpId=13&&tqId=11174&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking
题解:一个入栈序列是有可能对应多个出栈序列的。这里就是使用一个栈来模拟出栈的顺序,看是否能匹配的上。
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
size_t pushi = 0,popi = 0;
//用入栈的方式来模拟出栈的过程
stack<int> st;
while(pushi < pushV.size())
{
st.push(pushV[pushi]);
//有可能栈已经为空了,此时你在st.top()可能会直接崩
while(!st.empty() && st.top() == popV[popi])
{
++popi;
st.pop();
}
++pushi;
}
//说明popi走到了最后
if(popi == popV.size())
return true;
else
return false;
}
};
还需要好好理解一下deque。