【BFS】学习
相关知识
BFS先找到的一定最短,但如果是加权的路就会出现问题,就应采用Dijkstra最短路径算法解决加权路径的最短路。
BFS可以解决:
1.从A点出发是否存在到达B的路径(DFS也可以做到
2.从A出发到达B的最短路径(如果数据小,20(数组行列数)以内,DFS也行
DFS、BFS的区别
(1条消息) 什么时候用DFS,什么时候用BFS?_dfs规模为多少时适合_yishuige的博客-CSDN博客
序号 |
BFS |
DFS |
1 |
BFS代表宽度优先搜索 |
DFS代表深度优先搜索 |
2 |
BFS(宽度优先搜索)使用队列数据结构来查找最短路径 |
DFS(深度优先搜索)使用栈数据结构 |
3 |
BFS更适合搜索更接近给定源的顶点 |
如果有远离源的解决方案,则DFS更适合 |
4 |
BFS首先考虑所有邻居,因此不适合用于游戏或拼图中的决策树。 |
DFS更适用于游戏或拼图问题。我们做出决定,然后探索有关该决定的所有路径。如果这一决定带来获胜局面,我们将停止。 |
5 |
当使用邻接表时,BFS的时间复杂度为O(V+E);当使用邻接矩阵时,BFS的时间复杂度为O(V^2),其中V表示顶点,E表示边。 |
当使用邻接表时,DFS的时间复杂度也是O(V+E),当使用邻接矩阵时,DFS的时间复杂度也是O(V^2),其中V表示顶点,E表示边。 |
实现方法 |
基本思想 |
解决问题 |
N规模 |
|
DFS |
栈/递归 |
回溯法,一次访问一条路,更接近人的思维方式, |
所有解问题,或连通性问题 |
不能太大,<=200 |
BFS |
队列 |
分治限界法,一次访问多条路,每一层需要存储大量信息 |
最优解问题,如最短路径 |
可以比较大,因为可以用队列解决,<=1000 |
简单迷宫问题
走迷宫
题面可以看这个:(1条消息) acwing——844. 走迷宫_suxiaorui的博客-CSDN博客
#include
#include
#include
#include
using namespace std;
#define x first
#define y second
const int N=110;
typedef pair PII;//存坐标
int n,m;
int g[N][N];//存地图
int dist[N][N];//存每个点到起点的距离
queue q;
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
int bfs(int x1,int y1)
{
memset(dist,-1,sizeof dist);//初始化数组dist全为-1
q.push({x1,y1}); //第一个点入队
dist[x1][y1]=0;//第一个进来的点是起点
while(!q.empty())
{
auto t=q.front();//取出队头
q.pop();
for(int i=0;i<4;i++)//遍历四个方向
{
int a=t.x+dx[i];
int b=t.y+dy[i];
if(a<1||a>n||b<1||b>n) continue;
if(g[a][b]!=0) continue;
if(dist[a][b]>0) continue;//判断是否访问过
q.push({a,b});//压入满足条件的点
dist[a][b]=dist[t.x][t.y]+1;
if(a==n&&b==m) return dist[n][m];//到达了终点,直接返回距离
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i>g[i][j];
}
}
int res=bfs(1,1);
cout< 这里发现头文件cstring和string竟然是不一样的,memset要用ctring。
理一理思路:
先把起点放队列里,
只要队列里有数就弹出头结点,然后遍历头结点的四个方向,如果有点满足题目条件,就压入队列中;同时更新满足条件的点的dist,当点到达终点时直接退出循环,并返回dist。
离开中山路
P1746 离开中山路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include
using namespace std;
const int N=1e3+10;
#define x first
#define y second
typedef pair PII;
int n;
int x,y,x2,y2;
char g[N][N];//输入没有空格所以用char类型
int dist[N][N];//存距离
queue q;
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
int bfs(int x,int y)//从第x个位
{
memset(dist,-1,sizeof dist);
q.push({x,y});
dist[x][y]=0;//起点赋值为0
while(!q.empty())//遍历四个方向
{
auto t=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int a=t.x+dx[i];
int b=t.y+dy[i];
if(a<1||b<1||a>n||b>n) continue;//越界
if(g[a][b]!='0') continue;//此路不通
if(dist[a][b]>=0) continue;//已经走过了
q.push({a,b});//符合条件就压入队列
dist[a][b]=dist[t.x][t.y]+1;
if(dist[x2][y2]>0) return dist[x2][y2];
}
}
return -1;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",g[i]+1);//注意,天坑
//我们存的地图是要从(1,1)开始的,
//这里i从1开始可以确保行从1开始
//需要列从1开始,就需要g[i]+1
}
scanf("%d%d%d%d",&x,&y,&x2,&y2);
int res=bfs(x,y);
cout< 这题写的真有点受不了,一开始定义的变量是x1,y1,x2,y2,在dev上能正常运行,但洛谷和acwing就是编译错误。
呵呵,最后google才知道y1是一个关键字,有点无语就是说。
记住以后定义变量不要叫y1就好
C++中的那些报错之“[Error] ‘int y1‘ redeclared as diffrent kind of symbol”_XIOAGANG666的博客-CSDN博客
马的遍历
P1443 马的遍历 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这题就是一个bfs,不多说
#include
using namespace std;
const int N=1e3+10;
#define x first
#define y second
typedef pair PII;
int n,m,x,y;
queue q;
int dist[N][N];
int dx[]={-2,-1,1,2,2,1,-1,-2};
int dy[]={1,2,2,1,-1,-2,-2,-1};
void bfs(int x,int y)
{
memset(dist,-1,sizeof dist);
q.push({x,y});
dist[x][y]=0;
while(!q.empty())
{
auto t=q.front();
q.pop();
for(int i=0;i<8;i++)
{
int a=t.x+dx[i];
int b=t.y+dy[i];
if(a<1||b<1||a>n||b>m) continue;
if(dist[a][b]>=0) continue;
q.push({a,b});
dist[a][b]=dist[t.x][t.y]+1;
}
}
}
int main()
{
scanf("%d%d%d%d",&n,&m,&x,&y);
bfs(x,y);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
printf("%d ",dist[i][j]);
}
cout< 数组模拟队列
stl中都提供了queue,为什么还要手写数组来模拟队列呢?
答案很简单,在算法竞赛中,这样会比较快
用hh和tt双指针指向头结点和尾节点 队列特性 头删尾插
hh一般初始化为0,tt可以为-1或0,转化也比较简单,不多说了。
#include
using namespace std;
const int N=1e3+10;
#define x first
#define y second
typedef pair PII;
int n,m,x,y;
//queue q;
PII q[N*N];//PII类型的数组模拟队列
int dist[N][N];
int dx[]={-2,-1,1,2,2,1,-1,-2};
int dy[]={1,2,2,1,-1,-2,-2,-1};
void bfs(int x,int y)
{
memset(dist,-1,sizeof dist);
q[0]={x,y};
dist[x][y]=0;
int hh=0,tt=0;//分别指向头结点和尾节点
while(hh<=tt)
{
auto t=q[hh];
hh++;//出队
for(int i=0;i<8;i++)
{
int a=t.x+dx[i];
int b=t.y+dy[i];
if(a<1||b<1||a>n||b>m) continue;
if(dist[a][b]>=0) continue;
q[++tt]={a,b};//尾插
dist[a][b]=dist[t.x][t.y]+1;
}
}
}
int main()
{
scanf("%d%d%d%d",&n,&m,&x,&y);
bfs(x,y);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
printf("%-5d",dist[i][j]);
}
cout< 好奇怪的游戏
P1747 好奇怪的游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
主要思路是从(1,1)开始走,直接输出马起点的dist就行了
这题如果边界是00,就只有80分,改成11,才能AC
#include
using namespace std;
#define x first
#define y second
const int N=30;
typedef pair PII;
int p1,p2,p3,p4;
PII q[N*N];
int dist[N][N];
int hh=0,tt=-1;
int dx[]={-2,-2,-1,1,2,2,2,2,1,-1,-2,-2};
int dy[]={1,2,2,2,2,1,-1,-2,-2,-2,-2,-1};
void bfs()
{//头删尾插
memset(dist,-1,sizeof dist);
q[++tt]={1,1};//从11开始
dist[1][1]=0;
while(hh<=tt)
{
auto t=q[hh++];
for(int i=0;i<12;i++)
{
int a=t.x+dx[i];
int b=t.y+dy[i];
if(dist[a][b]>=0) continue;//走过就不再走了
if(a<1||b<1||a>20||b>20) continue;
dist[a][b]=dist[t.x][t.y]+1;
q[++tt]={a,b};
}
}
return;
}
int main()
{
cin>>p1>>p2>>p3>>p4;
bfs();
cout< Bronze Lilypad Pond B
P2385 [USACO07FEB]Bronze Lilypad Pond B - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include
using namespace std;
#define x first
#define y second
const int N=40;
typedef pair PII;
PII start,end1;
PII q[N*N];
int hh=0,tt=-1;
int m,n,m1,m2;//M,N的矩阵,移动格数
int g[N][N];//存图
int dist[N][N];
void bfs()
{//头删尾插
memset(dist,-1,sizeof dist);
int dx[]={m2,m1,m1,-m2,-m2,-m1,-m1,-m2};
int dy[]={m1,m2,-m2,m1,-m1,-m2,m2,m1};
q[++tt]=start;
dist[start.x][start.y]=0;
while(hh<=tt)
{
auto t=q[hh++];
for(int i=0;i<8;i++)
{
int a=t.x+dx[i];
int b=t.y+dy[i];
if(a<1||b<1||a>m||b>n) continue;//越界结束
if(dist[a][b]>=0) continue;//走过就结束
if(g[a][b]==0||g[a][b]==2) continue;//只有0和2不能走
q[++tt]={a,b};
dist[a][b]=dist[t.x][t.y]+1;
if(end1.x==a&&end1.y==b) return;
}
}
return;
}
int main()
{
scanf("%d%d%d%d",&m,&n,&m1,&m2);
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
scanf("%d",&g[i][j]);
if(g[i][j]==3) start={i,j};
if(g[i][j]==4) end1={i,j};
}
}
bfs();
cout< 有三个点一直WA真绷不住了
后续,我看了一中午给人心态看崩了,给大佬一眼看出来方向向量写错了,蒟蒻就是蒟蒻
AC代码
#include
using namespace std;
#define x first
#define y second
const int N=40;
typedef pair PII;
PII start,end1;
PII q[N*N];
int hh=0,tt=-1;
int m,n,m1,m2;//M,N的矩阵,移动格数
int g[N][N];//存图
int dist[N][N];
void bfs()
{//头删尾插
memset(dist,-1,sizeof dist);
int dx[]={m2,m1,m1,-m2,-m2,-m1,-m1,m2};
int dy[]={m1,m2,-m2,m1,-m1,-m2,m2,-m1};
q[++tt]=start;
dist[start.x][start.y]=0;
while(hh<=tt)
{
auto t=q[hh++];
for(int i=0;i<8;i++)
{
int a=t.x+dx[i];
int b=t.y+dy[i];
if(a<1||b<1||a>m||b>n) continue;//越界结束
if(dist[a][b]>=0) continue;//走过就结束
if(g[a][b]==0||g[a][b]==2) continue;//只有0和2不能走
q[++tt]={a,b};
dist[a][b]=dist[t.x][t.y]+1;
if(end1.x==a&&end1.y==b) return;
}
}
return;
}
int main()
{
scanf("%d%d%d%d",&m,&n,&m1,&m2);
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
scanf("%d",&g[i][j]);
if(g[i][j]==3) start={i,j};
if(g[i][j]==4) end1={i,j};
}
}
bfs();
cout< 多源BFS
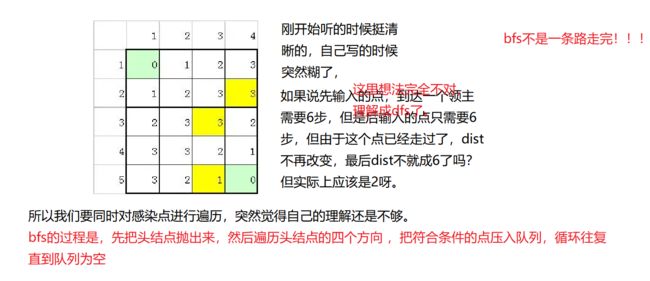
血色先锋队
P1332 血色先锋队 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include
using namespace std;
const int N=510;
#define x first
#define y second
typedef pair PII;
PII q[N*N];//数组模拟队列
int n,m,a,b;//n行m列 ,a个感染源,b个领主
int dist[N][N];
int hh=0;
int tt=-1;
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
//先对每个感染源进行入队,然后bfs,然后直接输出领主位置的dist
void bfs()
{//已经入队完毕了,直接弹出头结点
while(hh<=tt)//尾插头删
{
auto t=q[hh++];//弹出头结点
for(int i=0;i<4;i++)
{
int a=t.x+dx[i];
int b=t.y+dy[i];
if(a<1||b<1||a>n||b>n) continue;//越界就结束
if(dist[a][b]>=0) continue;
q[++tt]={a,b};//插入新节点
dist[a][b]=dist[t.x][t.y]+1;
}
}
}
int main()//尾插头删
{
memset(dist,-1,sizeof dist);
scanf("%d%d%d%d",&n,&m,&a,&b);
while(a--)
{//输入感染源位置
int c,d;
scanf("%d%d",&c,&d);
q[++tt]={c,d};//先入队
dist[c][d]=0;
}
bfs();
while(b--)
{
int c,d;
scanf("%d%d",&c,&d);//输入领主位置,直接输出其dist
printf("%d\n",dist[c][d]);
}
return 0;
} 矩阵距离
173. 矩阵距离 - AcWing题库
本篛狗不会,直接copy
思路
这道题就是求每一个点距离1的最短曼哈顿距离。
如果我们分别对每一个点求答案的话,肯定会超时,于是我们反向思考,直接从所有的1向整张图搜索。同时更新一下答案。
#include
#include
#define x first
#define y second
using namespace std;
typedef pair PII;
const int N = 1010;
const int dx[] = {0,0,1,-1},dy[] = {1,-1,0,0};
int n,m;
bool g[N][N];
int dist[N][N];
void bfs () {
queue q;
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= m;j++) {
if (g[i][j]) q.push ({i,j});
}
}
while (q.size ()) {
PII t = q.front ();
q.pop ();
for (int i = 0;i < 4;i++) {
int a = t.x + dx[i],b = t.y + dy[i];
if (a < 1 || a > n || b < 1 || b > m || g[a][b] || dist[a][b]) continue;
dist[a][b] = dist[t.x][t.y] + 1;
q.push ({a,b});
}
}
}
int main () {
cin >> n >> m;
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= m;j++) {
char ch;
cin >> ch;
g[i][j] = ch - '0';
}
}
bfs ();
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= m;j++) cout << dist[i][j] << ' ';
cout << endl;
}
return 0;
} 染色问题
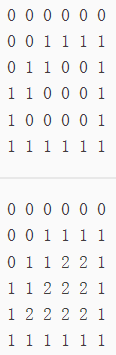
填涂颜色【最大联通子集
P1162 填涂颜色 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
乍看可能有点迷糊,但是仔细观察可以发现这题就是把0元素的联通集替换成2;
//这题的思路是把所有能走的0都走一遍且不走1
//那么剩下的没走的且不为1的地方就是需要涂色的点
//同时,会有特殊情况,如果我们从(1,1)开始走
//如果(1,1)正好就是1,那么我们就没法走了
//因此我们从(0,0)开始走,可以保证有一个闭合的0圈#include
using namespace std;
#define x first
#define y second
const int N=40;
typedef pair PII;
int n;
int g[N][N];//存地图
bool st[N][N];//只需要知道有没有走过就行
PII q[N*N];
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
int hh=0;
int tt=-1;
//这题的思路是把所有0都走一遍且不走1
//那么剩下的没走的地方不是1就是需要涂色的点
//同时,会有特殊情况,如果我们从(1,1)开始走
//如果(1,1)正好就是1了,那么我们就没法走了
//因此我们从(0,0)开始走,可以保证有一个闭合的0圈
void bfs(int x,int y)
{//队列尾插头删
q[++tt]={x,y};//插入
st[x][y]=true;
while(hh<=tt)
{
auto t=q[hh++];
for(int i=0;i<4;i++)
{
int a=dx[i]+t.x;
int b=dy[i]+t.y;
if(a<0||b<0||a>n+1||b>n+1) continue;
if(st[a][b]) continue;//已经走过了就不走了
if(g[a][b]!=0) continue;//只走0
q[++tt]={a,b};
st[a][b]=true;//把所有能走的全都标记
}
}
return;//走完了就return
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
scanf("%d",&g[i][j]);
}
}
bfs(0,0);
//涂色
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(!st[i][j]&&g[i][j]!=1) g[i][j]=2;
//没被访问过同时值不为1就涂色
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
printf("%d ",g[i][j]);
}
cout< 有外界干扰的迷宫问题【待补充
Meteor Shower S 有外界干扰的迷宫问题
P2895 [USACO08FEB]Meteor Shower S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
### 关于memset和0x3f
int a[100];
##### memset(a,0x3f,sizeof(a) );
0x3f=0011 1111=63
C++中**int**型变量所占的位数为**4个字节**,即32位
0x3f显然不是int型变量中单个字节的最大值,应该是0x7f=0111 1111 B
**那为什么要赋值0x3f ??**
int
##### 1.作为无穷大使用
因为4个字节均为0x3f时,0x3f3f3f3f的十进制是1061109567,也就是10^ 9级别的(和0x7fffffff一个数量级),而一般场合下的数据都是小于10^9的,所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。
##### 2.可以保证无穷大加无穷大仍然不会超限。
另一方面,由于一般的数据都不会大于10^9,所以当我们把无穷大加上一个数据时,它并不会溢出(这就满足了**“无穷大加一个有穷的数依然是无穷大”**),事实上0x3f3f3f3f+0x3f3f3f3f=2122219134,这非常大但却没有超过32-bit int_MAX的表示范围,所以0x3f3f3f3f**还满足了我们“无穷大加无穷大还是无穷大”的需求**。
首先要知道memset函数是**以字节为单位**进行赋值的;
**void *memset(void *s, int ch, size_t n);**
函数解释:将s中前n个字节 (typedef unsigned int size_t )用 ch 替换并返回 s 。
其实这里面的ch就是ascii为ch的字符;
将s所指向的某一块内存中的前n个 字节的内容全部设置为ch指定的ASCII值
#include
using namespace std;
#define xx first
#define yy second
const int N=310;
typedef pair PII;
int m;
int dist[N][N];//记录人走到某个位置的时间
int fire[N][N];//记录流星到达某个位置的时间
PII q[N*N];
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
//先输入流星位置,然后入队每个位置,bfs
//同时用fire保存其落地时间
//bfs搜索人走路的情况,同时用dist记录
// 如果在某个位置dist==fire就会被砸死,不走
int bfs()//模拟人走路的情况
{
q[0]={0,0};
dist[0][0]=0;
int hh=0,tt=0;
while(hh<=tt)
{
auto t=q[hh++];
for(int i=0;i<4;i++)
{
int a=t.xx+dx[i];
int b=t.yy+dy[i];
if(a<0||b<0) continue;
if(dist[a][b]) continue;
if(dist[t.xx][t.yy]+1>=fire[a][b]) continue;//会被砸死
dist[a][b]=dist[t.xx][t.yy]+1;
q[++tt]={a,b};
if(fire[a][b]>1e9) return dist[a][b];
//如果有点重复砸,取时间最早的那个
}
}
return -1;
}
int main()
{//尾插头删
cin>>m;
memset(fire,0x3f,sizeof fire);
while(m--)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
fire[x][y]=min(z,fire[x][y]);
//直接拓展落点的四个方向
for(int i=0;i<4;i++)
{
int a=x+dx[i];
int b=y+dy[i];
if(a<0||b<0||a>301||b>301) continue;
fire[a][b]=min(fire[a][b],z);
}
}
int res=bfs();
printf("%d",res);
return 0;
} 好难,看看别人写的。