半导体器件基础09:MOS管特性和应用(1)
说在开头:关于泡利不相容
又一次要聊到泡利不相容了,这说明它在量子论中是多么地重要。
泡利来到了哥本哈根理论物理研究所,玻尔给了他一个苦差事:研究反常赛曼效应。正常的赛曼效应光谱在磁场下会分裂成三条;可反常赛曼效应的光谱远多于三条,间距也不一致,这样用过去的计算方法就对不上了。泡利发现反常塞曼效应的光谱决定于最外层电子,里边轨道的电子都挤满了,而只要排满了就不会引起反常赛曼效应。玻尔老师说,电子总是喜欢占据能量最低的坑,那为什么大家不是都挤在最低的坑里呢?是什么导致了现在分层的排列方式?里德伯早先提出过原子核外的电子分布每层只能排下2n²个,n就是电子层数的取值,那2又是从哪里来的呢?这么多问题一股脑儿排在那里,泡利那聪明绝顶的脑袋也一时想不到答案。
泡利觉得电子应该还有一个现在还不知道的量子值,这个值具有二值性(举个栗子:电子不是负的,就是正的),那么电子就具有四个量子数:主量子数、磁量子数、角量子数,还有第四个量。但是第四个量子数到底是有什么物理含义呢?现在一时半会也没人搞明白。泡利就用他那聪明的脑瓜子想:不妨先假设一个量进去代到公式里算算看。这么一算,泡利就豁然开朗了。原来元素周期表是这么一回事。(泡利不相容的原则已经讲过好几次啦,具体请参考《关于PN结的那些事》中解释的泡利不相容原理)
泡利把他的成果告诉了大家,虽然元素周期问题得到了完美的解释,但是大家也有疑问:你到底能不能告诉我们,这第四个量到底是个啥东东?为什么只能取两个值?泡利自己也不知道这东西是啥玩意。但是有个人说他能说清楚,这家伙叫克罗尼格,他觉得这第四个量是电子的自旋。电子不仅绕着原子核公转,还有自转,他拿了狭义相对论计算了一番,然后就兴奋的跑去跟泡利说,泡利一听就又发挥出他那小钢炮本色:电子会自转,你老糊涂了吧?电子要是自转的话速度会远超光速。弄得这个克罗尼格灰头土脸,自卑不已,也就没有了信心写论文发表。过了半年,荷兰物理学家埃伦费斯特的两个学生:乌伦贝克和高斯密特,他们对老师提出这第四个量就是电子的自旋。埃伦费斯特一听,唉,这个想法不错啊,值得发表,赶快写论文去吧。这俩就屁颠屁颠跑去写了个豆腐干大小的文字,请老师推荐发给《自然》杂志,老师一看:一页都不到,字是少了一点,不过先发了再说吧。过了一个星期他们觉得还是放心不下,又去找了洛伦兹,洛伦兹老爷子辛苦了好几天给他们计算了下,脑袋都大了:要是电子会自旋,那么其表面速度将达到光速的10倍以上。这两位心都凉了,赶紧去找老师想把豆腐干要回来,要是发表出来,可就闹大笑话了。哪知他们的老师早就把论文寄出去了,还安慰他们:年轻人出点丑有啥要紧的,你们俩本来也没几个钱的面子,丢就丢吧。
论文一经发表,马上就有人表示赞同,谁这么没眼界啊?原来是二师兄海森堡。海森堡还给他们俩写了信,觉得他们的想法不错,就是里面的一个因子2有点问题,这俩人也答不上来。这时爱因斯坦刚好到莱顿大学讲学,正好碰上这俩年轻人,给他们指点了一番:这么计算就能把不同自旋方向的能量差给算出来了。泡利看到这篇论文,立刻火冒三丈:这玩意怎么又跑出来了?1926年,英国物理学家托马斯发现这些计算里有个小错误,修正了之后,就可以得到那个因子2,解决了海森堡的疑问。
其实粒子的自旋与宏观的自旋是完全不同的,大家开始以为粒子真的是像个陀螺一样自转,后来发现并不是这么回事。粒子的角动量是粒子的内禀特性,即这是粒子的本性之一,没法改变;自旋有半数自旋和整数自旋之分,一直到1940年泡利才把这事给搞清楚了。最亏的还是那个克罗尼格,他得知这个消息后,估计心里悔的有一万头草泥马奔过。
现在我们已经搞清楚了:电子的排列是有规律的,在原子同层轨道上没有任何两个电子可以拥有完全相同的量子态。泡利不相容可以扩展到一大类粒子:费米子(举个栗子:电子,质子,中子等);费米子的自旋都是半整数,自旋整数的叫做玻色子(举个栗子:光子,胶子等),玻色子不适用泡利不相容原理。泡利不相容原理算是旧量子论的最高成就了,不过旧量子论快就要混不下去了。(参考自:吴京平-无中生有的世界)
- MOS管参数
1. VGS(th):增强型MOS管的阈值开启电压,是在一定VDS条件下,开始出现ID电流时所需的VGS电压;
——不同的芯片,对VGS(th)的条件有所不同,如下图所示,VGS阈值电压是在一定测试条件下给出的,使用时需注意。
2. VGS(off):耗尽型MOS管的阈值关闭电压,是在一定VDS条件下,使得ID电流近似等于0时的VGS电压;
——同VGS(th)一样,厂家也是给出该值在特定测试条件下的值。
3. RGS(DC):在VDS=0时,VGS电压与IG电流的比值;
——该值表示MOS管的直流输入电阻,经常用栅极电流表示。
4. gm(gfs):低频夸导,VDS为常数时,D极电流的微变量与引起这个变化的VGS电压微变量之比;跨导是衡量MOS管VGS电压对ID电流控制能力的一个重要参数;
——单位VGS变化引起的ID极电流变化,单位为S,例如gfs=3S,表示:VGS变化1V,那么漏电流会增加3A;该参数会用于开关电源电路、缓启动电路MOS管的开启过程分析。
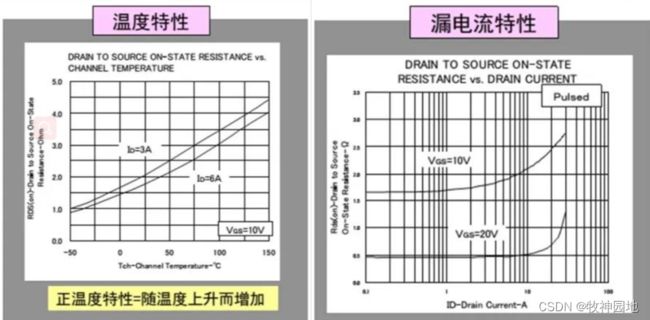
5. RDS(on):MOS管处于导通状态下的等效阻抗,导通电阻越大,则开启状态下的损耗越大;
——如上一章节分析,RDS(on)是MOS管在未进入饱和区之前的导通阻抗,此时MOS管DS两端的电压,随着电流线性增加,我们将VDS随ID增加的斜率等效成一个电阻;
1, 如下图所示,RDS(on)呈正温度特性:随温度的上升,电阻增加;温度上升对沟道“自由电子”电荷浓度影响不大,但会增加原子振动频率和幅度,阻碍电流;温度特性更近于金属;
2, RDS(on)电阻大小与施加在GS的电压成反比,GS电压越大,则沟道中“自由电子”电荷浓度增加,导通阻抗变小。
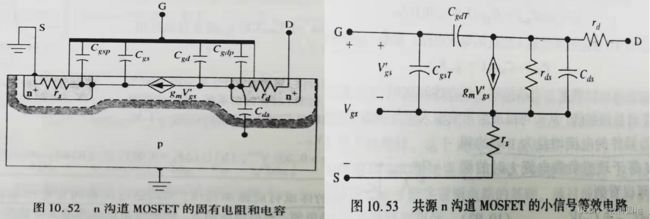
6. MOS管寄生电容容量值越小,Qg越小,开关速度越快,开关损耗越小;如同金属-氧化物-半导体电容是MOS管结构的核心,MOS管寄生电容和QG是MOS管应用的核心;
——寄生电容是MOS管结构中不可避免会存在的,主要是G极与衬底以及和S、D端之间的寄生电容;如下图所示,我们可以清晰的看到MOS结构中各寄生电容,不同结构MOS管之间有很大的差别。
1, CGS:G极与S极之间,以及G极与衬底之间靠近S端的平板电容之和;
2, CGD:G极与D极之间,以及G极与衬底之间靠近D端的平板电容之和;
3, CDS:由于S与衬底连接,所以CDS为D端与衬底之间的PN结电容。
4, Ciss:输入电容;将S和D极短接,测试G和S之间电容,zCiss=CGS+CGD;当输入电容充电/放电至阈值电压后,MOS管才能开启/关断;
——Ciss会增加驱动功率,高频应用时会影响开关速度,降低驱动电路的输出阻抗有利于提高输出电流,提高开关速度。
5, Coss:输出电容;将S和G短接,测试D和S之间电容,Coss=CDS+CGD;
6, Crss:反向传输电容;测试D和G之间电容,Crss=CGD;该电容称为米勒电容,它影响开关的上升/下降时间,关断延时时间。
——米勒电容的大小决定了MOS管开关时米勒平台时间的长短,米勒平台对于MOS管来说,是内部损耗较大的一个阶段(下面章节分析)。
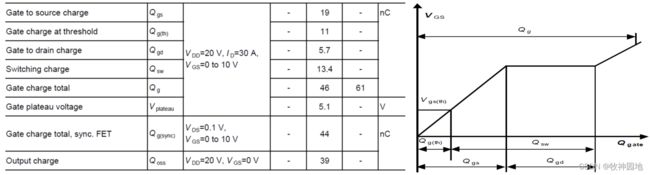
7, QG:G极的总电荷量,MOS管达到导通状态时所需的电荷量;
——既然已经有CGD,CGS参数,而Q=C*V,就能轻松计算Q的值,为什么需要单独的Q参数?这个问题值得深入思考;事实上通过后续MOS缓启动电路开启过程的分析,我们就会知道:QGD与CGD和QGS与CGS之间的关系是存在实际物理意义上差别的,不可等价计算。
8, QGS:G极/S极之间所需的电荷量;
——打开MOS管并使MOS管达到最大通流能力所需的电荷量,后续章节具体分析。
9, QGD:G极/D极之间所需的电荷量;
——QGD决定了米勒平台维持时间,后续章节具体分析。
10, Q = C*V,开关时间t=Q/I,电荷容量越大,所需的开关时间T也越大,开关损耗越大。
——开关损耗,主要是MOS管在开启或关闭时间段内,由于此时MOS管存在大电流,且DS之间存在高压降,所以存在较大的损耗,减小损耗的关键在于:缩短开关过程时间。
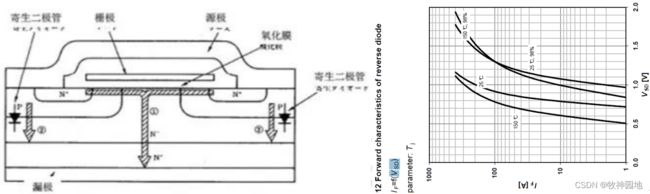
7. MOS管内部寄生二极管;
——我们从“MOS管原理”章节知道寄生二极管对于MOS管来说是不可避免的,所以它必然会导致MOS管某一方向的导通性,例如NMOS寄生二极管方向是:S->D;PMOS寄生二极管方向就是:D->S;在实际应用中,必须注意到这一点,否则MOS管将变成二极管,失去它应有的“可控开关”作用。
1, 当G/S极电压VGS=0V时,取决于内部二极管的正向V-I特性;
2, 当G/S极电压VGS加正向偏压,即MOS管处于导通状态时,与导通阻抗特性一致。
——二极管的V-I特性与MOS管本身是否正常开启有关,如果MOS管没有开启(VGS
8. IDSS:D极与S极之间的漏电流,VGS=0V,D与S之间加VDDS;
9. IGSS:G极与S极之间的漏电流,VDS=0V,G与S之间加VGSS;
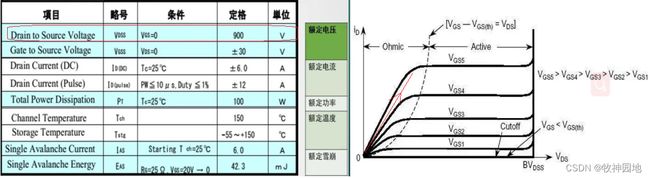
10. IDM:脉冲D极电流,反映器件处理脉冲电流的高低,对于一定的VGS电压,MOS管导通后,存在最大的漏电流。如下图,如果工作点位于可变电阻区域内,漏电流增大,会提高VDS电压,因此增加导通损耗,长时间工作会导致器件失效;
11. V(BR)DSS:在特定温度和GS短接情况下,流过D极电流达到一个特定值时的DS电压,雪崩击穿电压,V(BR)DSS是正温度系数;
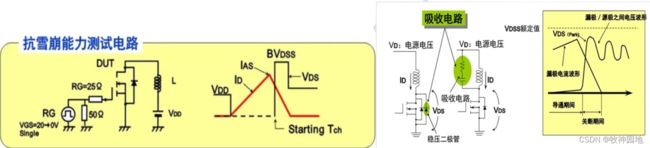
12. IAS:单发雪崩电流,峰值漏极电流;
13. EAS:单发雪崩能量,一次雪崩期间所能承受的能量极限(Tch<150c);
14. EAR:连续雪崩能量,所能承受反复出现雪崩的能力极限(Tch<150c);
——MOS管的本质也是由PN结构成,所以必然会存在加反压造成雪崩的情况,雪崩不造成器件损坏的必要条件是:其结电压不能超过最大允许电压。
15. Tch:MOS管沟道上限温度;
16. Tstg:器件保存温度范围;
17. Rthjc/Rthja:器件热阻,表示热传导难易程度,热阻值越小,表示散热性能越好;如果没有相关参数,可以用右侧公式估算;
——我们可以将热阻等价成电阻,热耗等价成电流,温度等价成电压;那么我们将得到一个公式:T(j-c) = Rthjc * P;这就是稳态系统散热的计算公式。